Романюк В.А. Основы радиосвязи. Учебное пособие В. А. Романюк

• Название: Учебное пособие В. А. Романюк
• Анкор: Романюк В.А. Основы радиосвязи.doc
• Дата: 16.03.2018
• Размер: 1.41 Mb.
• Имя файла: Романюк В.А. Основы радиосвязи.doc
• Тип: Учебное пособие; #16756
• страница: 5 из 7

=, где -угол между векторами , то

Учитывая связь напряженности электрического поля Е с потенциалом ц, запишем

В результате, принимая во внимание (2.22), получим

или, обозначив
ц2-ц1=

В пределе при окончательно запишем
(2.23)
Переход от к .

Воспользуемся определением силы тока
(2.24)

где q-заряд,
q=CU, C=C1.
Связь сила тока I с плотностью тока определяется следующим соотношением
(2.25)
Выберем в качестве поверхности интегрирования цилиндрическую поверхность, охватывающую внутренний проводник коаксиальной линии (рис.2.9)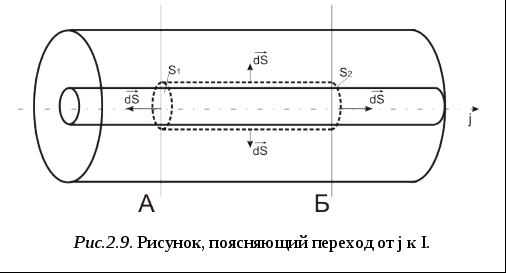

Тогда (интеграл по боковой поверхности равен 0).

Из (2.21) получаем


Окончательно при переходе к пределу при z имеем
(2.26)
Уравнения (2.23) и (2.26) называют телеграфными. Их решение дает возможность найти ток I и напряжение U как функции времени и координаты Х.
2.10 Решение телеграфных уравнений.
Продифференцировав уравнения (2.23) по координате, а уравнение (2.26) по времени и исключив ток I, получим волновое уравнение для напряжения U:
(2.27)
Будем полагать для простоты, что к линии подводятся колебания одной частоты . Тогда решение выражения (2.27) может быть записано в виде монохроматических волн
(2.28)
где первое слагаемое представляет собой волну, бегущую по линии в положительном направлении оси Х, её называют падающей. Второе слагаемое описывает отражённую волну, распространяющуюся в отрицательном направлении оси Х.

В решении (2.28) - комплексные амплитуды падающей и отраженной волн, - постоянная распространения


-скорость волны в линии

Волновое уравнение может быть записано и для тока

его решение имеет вид

Как было отмечено в разделе 1.7, монохроматические волны удобно представлять в виде комплексных амплитуд

Связь между и можно получить, подставив в первое телеграфное уравнение (2.23) мгновенные значения напряжения и тока в линии.

В результате будем иметь
(2.29)
- волновое сопротивление линии.
Аналогично можно найти связь с :
(2.30)
2.11 Режимы работы линий передачи
Допустим к входу линии передачи длиною подключен источник гармонического напряжения частотой , амплитудой , а в конце линии имеется нагрузка сопротивлением zн (рис.2.9).

Режим бегущей волны

Если в линии отсутствует отраженная волна, то имеем режим бегущей волны

Как видим, в любом сечении z линии передачи имеются колебания напряжения U(t) с одинаковой амплитудой Uпад и колебания тока I(t) с не изменяющейся амплитудой Iпад

Мгновенная фаза колебаний

зависит от координаты.

Особенностью режима бегущей волны является постоянство сопротивления линии при любых х:

Получим выражение для средней по времени мощности колебаний в режиме бегущей волны:
(2.31)
Мгновенные значения напряжения и тока в линии


Подставив эти выражения в (2.31), получим
.

Режим стоячих волн.

Допустим, в линии имеется отраженная волна, амплитуда которой равна амплитуде падающей волны

В этом случае напряжение в линии

После некоторых преобразований получим
(2.32)
Как видим, в этом случае колебания напряжения в линии происходят синфазно, независимо от координаты х. Амплитуда колебаний изменяется вдоль линии по закону косинуса (рис.2.10)

где - длина волны в линии.

Можно получить аналогичные выражения для тока в линии

или
(2.33)
Амплитуда колебаний тока также меняется в зависимости от х (рис.2.10).

Распределение амплитуд U и I о линии изображено на рис. 2.10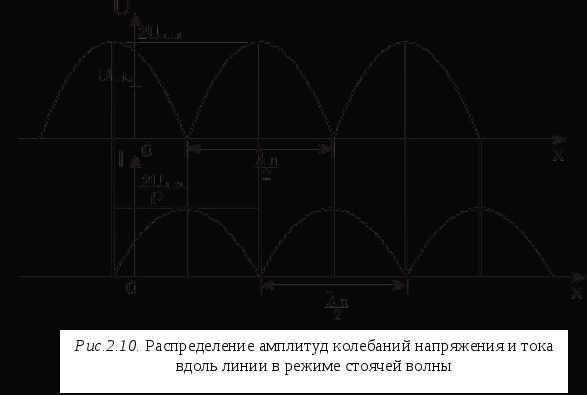

Нетрудно заметить, что имеются ечения в линии, где амплитуда колебаний максимальна, она в 2 раз больше амплитуды источника. Эти сечения называются пучностями. В других сечениях колебания отсутствуют, это - узлы. Пучности (а также узлы) отстают друг от друга на расстояние , равное , где -длина волны в линии.

Получим выражение для средней мощности колебаний в линии. С этой целью подставим в (2.31) выражения (2.32) и (2.33), в результате имеем Рср=0. Итак, в режиме стоячих волн энергия вдоль линии не передается. Таким образом, режим стоячих волн для передачи радиоволн не пригоден. Этот режим применяют в резонаторах. Режим смешанных волн.

На практике в линии всегда присутствует отраженная волна, причем амплитуда отраженной волны Uотр меньше амплитуды падающей Uпад. Допустим, что Uотр = , т.е. фаза напряжения отраженной волны цотр=0. Комплексная амплитуда напряжения в линии
.
Распределение амплитуды напряжений вдоль линии показано на рис.2.11.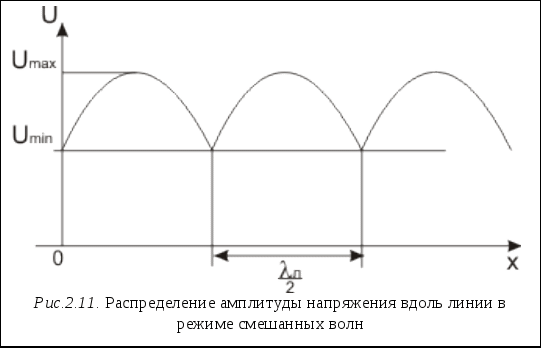

В некоторых сечениях линии (пучностях) имеется усиливающая интерференция, падающая и отраженные волны складываются в фазе и амплитуда колебаний напряжения максимальна . В других сечениях (узлах) - гасящая интерференция, волны складываются в противофазе. Здесь амплитуда напряжений минимальна .

2.12 Коэффициент стоячей волны напряжения
Коэффициент отражения.

Для характеристики режима работы линии используют коэффициент стоячей волны напряжения , который определяется так
(2.34)
Поскольку
, , то
(2.35)
Коэффициент отражения.

Другим коэффициентом, применяемым для оценки режима работы линии, является коэффициент отражения напряжения от нагрузки :

Так как при
x=
(2.36)
где
- модуль коэффициента отражения;
- фаза коэффициента отражения.
Связь kсв c Г.

Из (2.35) и (2.36) следует, что
.(2.37)
Отсюда

Из (2.36) следует, что модуль коэффициента отражения может находиться в пределах

0<Г<1,

а согласно (2.37), пределы изменения коэффициента стоячей волны


2.13 Передача энергии в нагрузку
В режиме смешанных волн мощность электромагнитных колебаний, поступающая в нагрузку

где - мощность колебаний, создаваемых падающей волной; - мощность колебаний отраженной волны, причем

где - проводимость нагрузки.

Отсюда
,
или
(2.38)
Таким образом, мощность электромагнитных колебаний, передаваемых по линии от источника к нагрузке, в значительной мере зависит от модуля коэффициента отражения Г.

Максимальная мощность, передаваемая в нагрузку.

В любой линии передачи существует максимально допустимая амплитуда колебаний . Допустим, что в предельном случае выполняется условие где

максимальная амплитуда колебаний в линии, т.е амплитуда в пучностях.

В этом случае

и мощность колебаний падающей волны

Подставив это выражение в (2.38), получим с учетом (2.37)
(2.39)
Из (2.39) следует, что при заданной амплитуде для максимальной передачи мощности в нагрузку следует уменьшать , т.е. стремится к установлению режима бегущих волн.
2.17 Условия существования режима бегущих волн
Как было отмечено в разделе 2.13, для наиболее эффективной передачи энергии электромагнитных колебаний по линии от источника к нагрузке следует устанавливать режим бегущих волн. Получим условие его существования.

В конце линии при сопротивление нагрузки

где

Учитывая (2.27) и (2.28), запишем

или, поделив числитель и знаменатель на и принимая во внимание выражение (2.36), получим

отсюда
(2.40)
В режиме бегущих волн коэффициент отражения напряжения . Таким образом, получаем следующие условия для существования режима бегущих волн: (2.41) или где - волновое сопротивление линии,

Для того, чтобы в линии передачи существовал режим бегущих волн, требуется, чтобы нагрузка была чисто активная и сопротивление нагрузки равнялось волновому сопротивлению линии.

Волновое сопротивление зависит от погонных параметров линии