Романюк В.А. Основы радиосвязи. Учебное пособие В. А. Романюк

• Название: Учебное пособие В. А. Романюк
• Анкор: Романюк В.А. Основы радиосвязи.doc
• Дата: 16.03.2018
• Размер: 1.41 Mb.
• Имя файла: Романюк В.А. Основы радиосвязи.doc
• Тип: Учебное пособие; #16756
• страница: 2 из 7

Итак, в идеальном диэлектрике при сделанных допущениях решением уравнений Максвелла являются электромагнитные волны, движущиеся вдоль оси z в прямом и обратном направлениях со скоростью v. Прямая волна распространяется от источника электромагнитных колебаний, а обратная возникает при наличии отражений.
1.4 Энергия электромагнитного поля
Если в пространстве существует электромагнитное поле, то в произвольном объеме V имеется энергия
,
где

плотность электрической энергии Дж/м3,

плотность магнитной энергии, Дж/м3 .

Поскольку электромагнитное поле существует в виде волн, поле будет перемещаться в пространстве. В частности, энергия будет выходить или входить в объем V. Для оценки энергии электромагнитных волн введена физическая величина, называемая вектором Пойнтинга и равная векторному произведению векторов и :
,Вт/м2.
Величина вектора Пойнтинга
,

где б – угол между векторами и . В идеальном диэлектрике П = EH.

Вектор Пойнтинга п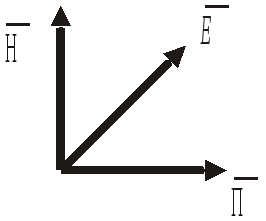ерпендикулярен плоскости расположения векторов и и его направление определяется «правилом винта» при вращении к по кратчайшему расстоянию (рис.1)

Р

Рис.1.1 Взаимная ориентация векторов , и


азмерность величины вектора - Вт/м2. Поэтому П – это энергия электромагнитного поля, проходящая в единицу времени через поверхность единичной площади, т.е. плотность потока мощности.

Энергия электромагнитного поля, выходящая из объема V в единицу времени, определяется формулой
,
где под интегралом – скалярное произведение векторов и , а интеграл берется по замкнутой поверхности S, ограничивающий объем V.

В случае, если диэлектрик в объеме V - неидеальный (), то возникают токи проводимости плотностью и, в соответствии с законом Джоуля – Ленца, часть энергии электромагнитного поля преобразуется во внутреннюю (тепловую) энергию диэлектрика.

Закон сохранения энергии определяется теоремой Пойнтинга:

-
где в левой части – скорость убывания энергии поля в объеме V, Pпот - количество теплоты, выделяющейся в 1 с в диэлектрике за счет протекания токов, т.е. мощность потерь, причем
,
где скалярное произведение - это плотность мощности потерь, т.е. количество теплоты, выделяемой в единицу времени.

В соответствии с теоремой Пойнтинга, изменение энергии электромагнитного поля в объему V происходит по 2-м причинам. Во - первых, за счет движения энергии в пространстве, во – вторых, за счет нагревания диэлектрика при протекании токов проводимости.
1.5 Монохроматические волны в идеальном пространстве
Радиосигнал представляет собой сложную зависимость величин E и H от времени, спектр сигнал содержит множество частот. Если сигнал узкополосный, то его спектр сосредоточен вблизи несущей частоты и можно, в первом приближении, полагать, что колебания E(t) и H(t) имеют гармоническую форму, т.е. спектр содержит только одну частоту f, Гц (или циклическую частоту , рад/с).

Электромагнитные волны, в которых спектр колебаний содержит одну частоту, называют монохроматическими. Введение понятия монохроматических волн существенно упрощает анализ.

Предположим, что колебания распространяются вдоль одной оси z, т.е. E(t,z) и H(t,z) - функции 2-х переменных: t и z. В некоторой точке пространства z = 0 имеется источник электромагнитного поля
,
где Em - амплитуда колебаний.

Аналогично изменяется во времени и H(t,0). Считаем, что источник колебаний создает поле, которое не меняется по координатам x и y. В точке напряженность электрического поля
,
где v- скорость распространения волны, или
(1.7)
Постоянная
(1.8)
называется фазовым множителем. Если учесть, что , а длина волны
,
то

(1.9)
и имеет другое название – волновой множитель, или волновое число.

Мгновенная фаза колебаний
(1.10)
- функция времени и координаты. Если объединить в пространстве все точки, в которых колебания синфазны, т.е. , то получим поверхность равных фаз. На этой поверхности в данный момент времени значения E одинаковы. Поверхность равных фаз называется волновой поверхностью. В рассматриваемом случае волновая поверхность является плоскостью, простирающейся в пространстве бесконечно вдоль координат y и x.

Вдоль координаты z плоскость движется со скоростью
,
называемой фазовой скоростью. Из (1.10) следует что

и фазовая скорость
,
т.е. совпадает со скоростью v, определяемой (1.3).

Итак, если источник поля создает гармонические колебания в плоскости z = 0, то в идеальном диэлектрике возникает плоская монохроматическая волна, у которой векторы и изменяются по закону
, (1. 11,а)
(1.11,б)
и сдвинуты в пространстве на угол 900, фазовая скорость волны равна
,
а связь амплитуд напряженностей электрического и магнитного полей подчиняются формуле (1.5). Запишем, в каком соотношении находятся энергии электрического и магнитного полей в плоской волне.

Плотность энергии электрического поля

и учитывая (1.5), получим

Таким образом, энергия плоской волны состоит из равных долей энергии электрического и магнитного полей.
1.6 Поляризация радиоволн
Электромагнитные волны бывают поляризованными и неполяризованными. Волны называются поляризованными, если направления векторов и в пространстве могут быть определены в любой момент времени. Если же направления и изменяются во времени случайным образом, то волна называется неполяризованной. Для радиосвязи естественно использовать поляризованные волны, что даёт возможность эффективного приёма радиосигналов при известном законе изменения и в пространстве.

Виды поляризации различаются законом изменения в пространстве плоскости поляризации, т.е. плоскости, проходящей через вектора 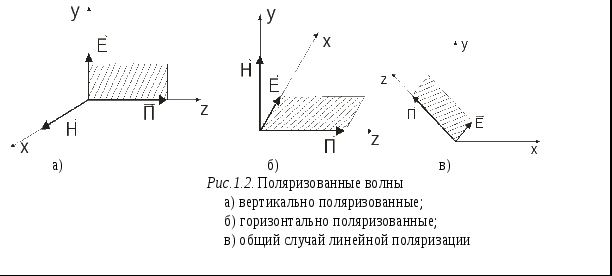и . Если плоскость поляризации остаётся неподвижной по мере распространения волны, то такая поляризация называется линейной. Примеры линейно поляризованных волн представлены на рис.1.2.

Вектор может быть расположен под углом к плоскости х или у. В этом случае он образован суммой двух векторов:

Если векторы иколеблются синфазно во времени, то поляризация остаётся линейной. Если же антенной (при z=0) возбуждаются колебания и, сдвинутые по фазе на ц=±90є, например

то суммарный вектор Е вращается. Конец вектора (а следовательно, и ) описывает окружность с центром в начале координат. Такая поляризация называется круговой.

В случае неравенства амплитуд колебаний 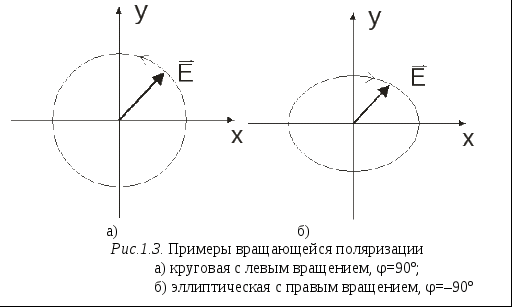и поляризация становится эллиптической - рис.1.3. Круговую и эллиптическую поляризацию называют также вращающейся с левым или с правым вращением.

При распространении волны с вращающейся поляризацией концы векторов и описывают в пространстве винтовые линии.
1.7 Представление монохроматических волн в виде комплексных. амплитуд
В случае монохроматических волн колебания в некоторой точке пространства имеют вид
(1.12)
Функцию такого вида можно рассматривать как действительную часть показательной функции , где i -мнимая единица. Действительно, в cоответствии с формулой Эйлера

Поскольку линейные операции – сложение, вычитание, дифференцирование и интегрирование над комплексными числами осуществляются раздельно для действительных и мнимых частей, можно заменить функцию функцией . При этом, совершая линейные операции над функцией, нужно помнить, что интересует преобразования лишь линейных частей.

Таким образом, вместо колебаний вида (1.12) будем пользоваться формой записи

где


комплексная амплитуда, т.е. величина, несущая информацию об амплитуде Em и начальной фазе ц гармонических колебаний.

Такая замена выгодна тем, что при линейных операциях над гармоническими функциями сохраняется множитель. Это очевидно в случае сложения и вычитания. Аналогично при дифференцировании и интегрировании функции

,

В результате множитель при преобразованиях гармонических функций можно отбросить и производить операции не над мгновенными значениями функций, а над комплексными амплитудами, что существенно упрощает анализ. При этом нужно помнить, что комплексная амплитуда производной функции равна комплексной амплитуде исходной функции, умноженной на Ящ, а операция интегрирования эквивалентна делению комплексной амплитуды исходной функции на Ящ.

Применяя метод комплексных амплитуд для бегущей волны вида

получим выражения для комплексной амплитуды бегущей волны
(1.13)
1.8 Радиоволны в диэлектрике с потерями энергии
Для монохроматических волн удобно записать уравнения Максвелла в комплексном виде:

где - комплексные амплитуды соответствующих физических величин.

Комплексная диэлектрическая проницаемость среды.

Учитывая (1.1), запишем для комплексных амплитуд

и первое уравнение Максвелла можно представить в виде

Величину
(1.14)
называют комплексной диэлектрической проницаемостью среды. Мнимая её часть указывает на свойство среды проводить электрический ток. Величину можно представить в виде вектора на комплексной плоскости (рис.1.4)

Тангенс угла наклона вектора