Романюк В.А. Основы радиосвязи. Учебное пособие В. А. Романюк

• Название: Учебное пособие В. А. Романюк
• Анкор: Романюк В.А. Основы радиосвязи.doc
• Дата: 16.03.2018
• Размер: 1.41 Mb.
• Имя файла: Романюк В.А. Основы радиосвязи.doc
• Тип: Учебное пособие; #16756
• страница: 4 из 7

, (2.5)
критическая частота
. (2.6)
В результате поле принимает вид бегущей волны
,
, (2.7)
,
где
.
Таким образом, в линиях передачи возможно существование бесконечного числа поперечно – магнитных волн типа Em, отличающихся числом m, которые распространяются вдоль оси z, если частота колебаний источника f > fкр.

Поперечные электромагнитные волны

Если в выражениях (2.7) и (2.6) установить m = 0, то получим поле, имеющее две взаимно перпендикулярные составляющие и . Такое поле называется поперечно электромагнитным, или поле ТЕМ – типа (Transverse Electro-Magnetic).

ТЕМ – волны существуют при любых частотах f, т.е fкр =0 и имеют такую же структуру, как поле в свободном пространстве.
2.3 Поперечно – электрические волны
Решая уравнения системы (2.2), получим выражение для составляющих поля поперечно электрического типа (ТЕ – или H – волны):
,
, (2.8)
,
где - амплитуда колебаний напряженности электрического поля прямой волны при z=0,

волновое сопротивление среды. Постоянная распространения определяется выражением (2.5), критическая частота fкр - формулой (2.6).

Как видно из (2.8), существует бесконечное число типов поперечно - электрических волн Hm, соответствующих разным m = 1,2,3,… При m = 0, все составляющие поля равны 0.

Так же как и поперечно – магнитные поля, H – волны распространяются вдоль оси z, если частота колебаний источника превышает критическую частоту fкр, определяемую выражением (2.6).
2.4 Фазовая и групповая скорости волн. Длина волны в линии
Фазовая скорость движения волн типа Em и Hm, т.е скорость распространения гармонических колебаний одной фазы, определяется выражением

Подставив сюда выражение (2.5) и получим
, (2.9)
где

скорость света в среде.

Как видим, фазовая скорость ТМ - и ТЕ – волн всегда больше скорости света. Следует отметить, что фазовая скорость E – и H – волн зависит от частоты колебаний f. Зависимость от f, называется дисперсией, а среда, в которой наблюдается дисперсия – дисперсионной. Таким образом, линии передачи, в которых распространяются поперечно – магнитные или поперечно – электрические волны являются дисперсными.

Помимо фазовой, для характеристики движения радиоволн применяют понятие групповой скорости . Групповая скорость введена для оценки движения радиосигнала.

Радиосигналом называются высокочастотные колебания, модулированные низкочастотными колебаниями, которые содержат информацию. Групповая скорость – это скорость перемещения информации. Одновременно, групповая скорость является скоростью перемещения энергии.

При движении радиосигнала имеем не монохроматическую волну, а волну, содержащую спектр частот. Если радиосигнал узкополосный, т.е. ширина спектра много меньше средней частоты щ, то групповая скорость определяется выражением [1]:
(2.10)
Выражение (2.10) можно применить и к линиям передачи, определяя тем самым, скорость перемещения энергии.

Если в линии распространяется ТЕМ – волна, для которой, то из (2.10) следует, что
,

т.е. равна скорости света v в однородной среде.

При распространении волн Em и Hm в формулу (2.10), вместо в, следует подставить фазовый множитель вm, определяемый выражением (2.5). В результате получим
(2.11)
Как видим, групповая скорость меньше скорости света в среде v. Объединяя выражения (2.9) и (2.11), запишем
(2.12)
Длина волны в линии

Как известно, длина волны в линии – это расстояние, проходимое волной за период колебаний T
,
где vопределяется выражением (2.9).

Если в линии распространяется ТЕМ-волна, то фазовая скорость равна скорости света в среде v. Поскольку
,
,


скорость света в вакууме, то
,
где , - относительные диэлектрическая и магнитная проницаемости диэлектрика, заполняющего линию, и длина волны в линии
,
где - длина волны в вакууме.

В случае распространения волн Em и Hm - типа
(2.14)
Из соотношений (2.13) и (2.14) следует, что уменьшается при заполнении линии диэлектриком или магнитным материалом, и увеличивается при возбуждении поперечно – магнитных и поперечно – электрических волн.
2.6 Затухающие электромагнитные поля
Если к линии подключен источник, генерирующий колебания, частота которых меньше критической, определяемой формулой (2.6), то система уравнений (2.1) имеет следующее решение (см. приложение 5):
(2.15)
где - зависящие от х амплитуды колебаний напряженностей поля в точке z=0

- действительное число,

Из (2.15) видно, что амплитуда колебаний, возбуждаемых в линии в точке z=0, уменьшается с ростом z, причем быстрота затухания тем больше, чем сильнее отличаются f от fкр. При любых z колебания синфазны, т.е. отсутствует движение волны.

Как следует из (2.15) колебания H(t) и E(t) происходят с фазовым сдвигом, равным 90, поэтому средний во времени вектор Пойнтинга равен 0, т.е. электромагнитное поле не переносит энергии.
2.7 Радиоволны в прямоугольном волноводе
Прямоугольный волновод (рис.2.5) - широко используемая линия передачи, обладающая наименьшими потерями энергии, по сравнению с другими типами линий.

Поперечным сечением волновода является прямоугольник, широкая сторона которого равна а, узкая-b.

Для нахождения электромагнитного поля внутри волновода следует решить уравнения Максвелла с граничными условиями



где - касательная составляющая напряженности электрического поля. Проведя преобразования, аналогичные тем, которые были проделаны при нахождении поля между параллельными плоскостями, найдем выражения для составляющих поля в волноводе. Здесь также имеются две группы полей:

- поперечно-электрические или ТЕ-типа (Н-тип),

- поперечно-магнитные или ТМ-типа (Е-тип).

Поле Н-типа имеют составляющие Ех, Еу, Нх, Ну, Нz, а поле Е-типа – Ех, Еу, Еz, Нх, Ну.

Радиоволны Н-типа

Поперечно-электрические поля имеют следующие составляющие:
(2.16)
(2.17)
Как видим, поле имеет вид бегущей волны при , где
(2.18)
В волноводе может распространяться бесконечное число волн Hmn, соответствующих разным значениям m и n. Для того чтобы расширить диапазон пропускаемых частот, следует, по возможности, уменьшить критическую частоту . С этой целью следует возбуждать волны, у которых m и n минимальны.

Как следует из выражений для составляющих поля, не существует волны Н00. Простейшими типами колебаний являются Н10 и Н01. Так как a>b, то из (2.18) следует, что наименьшая критическая частота у волн Н10. Именно она, главным образом, используется на практике.

Волна Н10

Подставим в (2.16) m=1, n=0, получим

где -постоянная распространения волн Н10, определяемая выражением (2.16), а критическая частота

Поскольку
,
где -критическая длина волны в диэлектрике, заполняющем волновод, то
.
Длина волны в волноводе определяется соотношением (2.14), справедливым для волн Н- и Е-типа.

На рис.2.6 приведено распределение линий напряженности Е и Н в случае возбуждения волн Н10.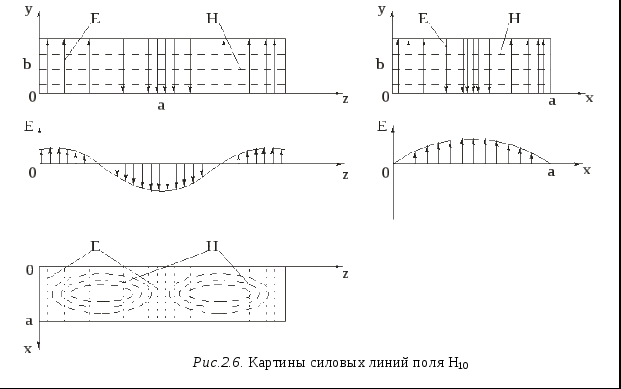

2.8 Волны ТЕМ-типа
К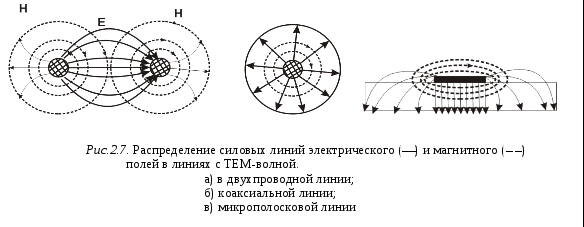


ак было отмечено в разделе 2.3, поперечные электромагнитные поля (ТЕМ-типа) существуют в линии при любых частотах колебаний, в том числе при , т.е. при протекании постоянного тока. Поэтому ТЕМ-волны могут распространяться в тех линиях, которые пропускают постоянный ток. Среди представленных на рис.2.1 это - двухпроводные, коаксиальные и микрополосковые линии.
На рис.2.7 изображены распределения электрических и магнитных линий в линиях с ТЕМ-волнами, справедливые для некоторого момента времени.

Помимо главной особенности таких ТЕМ-волн - отсутствие граничной частоты, эти волны имеют следующие свойства.

Фазовая скорость не зависит от частоты колебаний и равна скорости света в среде

где с- скорость света в вакууме. Для немагнитных сред (где )
(2.19)
В микрополосковой линии среда неоднородна по сечению, поэтому в (2.19) нужно подставить некоторую эффективную относительную диэлектрическую проницаемость , которая заключена в пределах ,где - относительная диэлектрическая проницаемость подложки. Значение для микрополосковых линий можно найти, например в работе .

Длина волны в линии не зависит от частоты колебаний f:

где - длина волны в вакууме. Для линий с немагнитным заполнением

(2.20)
Поскольку структура поля в линии такая же. как и при протекании постоянного тока, а статическое электрическое поле потенциально, то и для переменных полей можно использовать понятие потенциала . Это дает возможность перехода при расчете поля от дифференциальной векторной величины к интегральной скалярной величине, где U – разность потенциалов, или напряжение. В результате, вместо расчёта трех проекций вектора , зависящих от 4-х переменных, достаточно найти одну величину U как функцию 2-х переменных. Это значительно упрощает расчёт.

Вектор плотности тока в линиях с ТЕМ-волной имеет составляющую, направленную вдоль оси распространения (оси х). Поэтому, вместо дифференциальной векторной величины , можно перейти к интегральной скалярной величине – току I(t,x).
2.9 Телеграфные уравнения
Получим соотношение между напряжением U и током I в линии передачи с ТЕМ-волной, которые позволят анализировать распространение электромагнитной волны в линии, не решая уравнения Максвелла. С этой целью рассмотрим небольшой отрезок коаксиальной линии длинной (рис.2.8).

Полагаем, что потенциал в сечении А равен ц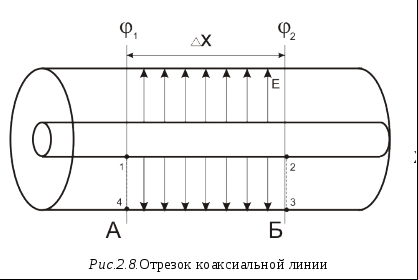, а в сечении В ц2. Линию считаем не имеющей потерь, обладающей погонной индуктивностью L1 и погонной емкостью С1 (L1, C1-это соответственно индуктивность и емкость линии длиною 1м).

Воспользуемся интегральной записью II уравнения Максвелла

где магнитный поток представим в виде
(2.21)
L - индуктивность отрезка линии длиной
(2.22)
Контур интегрирования 1-2-3-4 изображён на рис.2.8. Итак, с учётом (2.21)

Поскольку скалярное произведение векторов