Романюк В.А. Основы радиосвязи. Учебное пособие В. А. Романюк

• Название: Учебное пособие В. А. Романюк
• Анкор: Романюк В.А. Основы радиосвязи.doc
• Дата: 16.03.2018
• Размер: 1.41 Mb.
• Имя файла: Романюк В.А. Основы радиосвязи.doc
• Тип: Учебное пособие; #16756
• страница: 6 из 7

, которые определяются размерами линии и её заполнением. В большинстве радиотехнических устройств применяются коаксиальные и микрополосковые линии со стандартным волновым сопротивлением Ом или Ом. Такие значения сначала были выбраны для коаксиальных линий из условия минимума потерь в линии и максимума передаваемой мощности (см. Приложение 6). Поскольку в микроэлектронных радиосистемах коаксиальные линии сопрягаются с микрополосковыми, такой же стандарт был выбран и для микрополосковых линий.

В заключение отметим, при таком условии амплитуды колебаний напряжения и тока не зависят от того, в каком сечении в линии они определены. Изменения амплитуд объясняется сложением колебаний, распространяющихся вдоль оси Х и обратно, мгновенная фаза которых зависит от координаты. Из-за этой зависимости возникают пучности, где разница фаз падающей и отраженной волн равна 0 и узлы, где разность фаз составляет радиан. Для того, чтобы устранить эту зависимость, нужно выполнить условие или

где -длина волны в линии.

Таким образом, линии передачи и любые электронные каскады радиосистем, размеры которых значительно меньше длины волны, можем считать устройствами с сосредоточенными параметрами. Зависимость физических величин и параметров от координат в них не проявляется.
3. Излучение и распространение радиоволн
Электромагнитные волны излучаются в пространстве передающими антеннами, на которые поступают колебания по фидеру от источника. В антеннах происходит преобразования типа колебаний, существующего в фидере, в ТЕМ – волны, распространяющиеся в свободном пространстве.
3.1 Диполь Герца
Электромагнитное поле создается генератором, от которого колебания E(t) и H(t) по фидерному тракту поступают в излучатель антенны – рис. 3.1.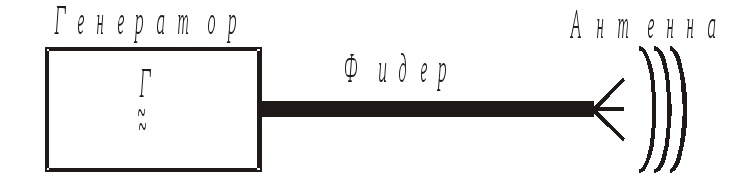


Рис.3.1. Образование электромагнитного поля в пространстве




Антенна – это устройство, которое служит для излучения и приема электромагнитных колебаний. Существует огромное количество типов антенн. Все они взаимны, т.е. одновременно могут излучать и принимать. Изучение антенн начнем с самых простых.

Простейшим излучателем является диполь Герца, представляющий собой металлический стержень, в разрыв которого поступают колебания от генератора Iг(t) , а на концах имеются шары.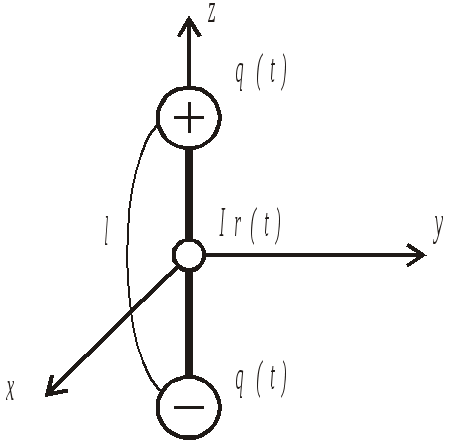


Рис.3.2 Диполь Герца




При периодическом изменении тока генератора в диполе протекает переменный ток плотностью j(t) , а на шарах накапливается переменный заряд q(t). Диполь Герца излучает электромагнитные колебания по следующим причинам:

в соответствии с 1 – м и 3 – м уравнениями Максвелла под действием переменных j(t) и с(t) в пространстве около диполя возникают переменные магнитное H(t) и электрическое E(t) поля;

в согласии с 1-м и 2-м уравнениями Максвелла вокруг силовых линий возникает магнитное поле , а вокруг силовых линий возникает поле ; далее процесс повторяется, в результате чего образуется электромагнитная волна, распространяющаяся в пространстве.

Для того, чтобы определить характеристики излучения диполя Герца, решим уравнения Максвелла при следующих допущениях:

плотность тока проводимости вибратора jпр(t) одинакова в любой точке сечения стержня, т.е. ток равномерно распределен по сечению площадью S, отсюда
;
ток генератора изменяется во времени по гармоническому закону

,
где - амплитуда, щ – циклическая частота колебаний.

Уравнения Максвелла целесообразно решать в сферической системе координат, где координатами являются: r - расстояние от начала координат до точки наблюдения, и - угол места, ц - азимутальный угол – рис.3.3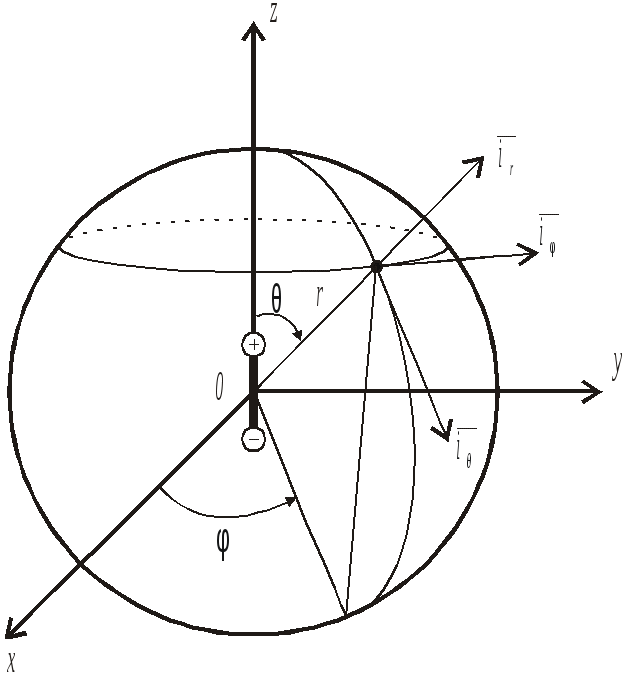


Рис.3.3 Сферическая система координат




Векторы и в сферической системе могут быть записаны следующим образом:
;
;
где , , - векторы единичной длины, направленые по касательной к координатным линиям; Er, Eи, Eц, Hr, Hи, Hц – проекции векторов и на направления r, и, ц.

Координатная линия – это линия пересечения двух координатных поверхностей. Координатные поверхности – поверхности одинаковых значений r, и, ц. Координатной поверхностью r = const является сфера, и = const - поверхность конуса, ц = const - плоскость.

Координатная линия r - прямая, образованная пересечениями конической поверхности и = const и плоскости ц = const , координатная линия и - окружность, образованная пересечением сферы r = const и плоскости ц = const , линия ц - окружность, образованная пересечением сферы r = const и поверхности косинуса и = const . На рис. 3.3 показаны направления векторов , и .

При расположении диполя Герца, показанном на рис. 3.3, составляющие поля не зависят от азимутального угла ц . Решение уравнений Максвелла при известной длине диполя l , амплитуде тока генератора Im, параметрах пространства е и м, при условии отсутствия потерь энергии имеет следующий вид [1]:
,
,(3.1)
,
где
- волновое сопротивление пространства,
- фазовый множитель.
Как видим, из шести проекций векторов и в решении оказалось только три.
3.2 Ближняя и дальняя зоны излучателя
Анализ полученных соотношений для проекций векторов показывает, что характер электромагнитного поля антенны существенно зависит от сомножителя . Произведение вr можно записать в виде
.
Ближняя зона

В точках пространства, расположенных вблизи излучателя, там, где выполняется соотношение



можно считать, что . Кроме того, можно еще более упростить выражение для комплексных амплитуд , и , пренебрегая в скобках слагаемыми высших порядков малости. Итак, для комплексные амплитуды
,
,

.
Мгновенные значения проекций векторов напряженности 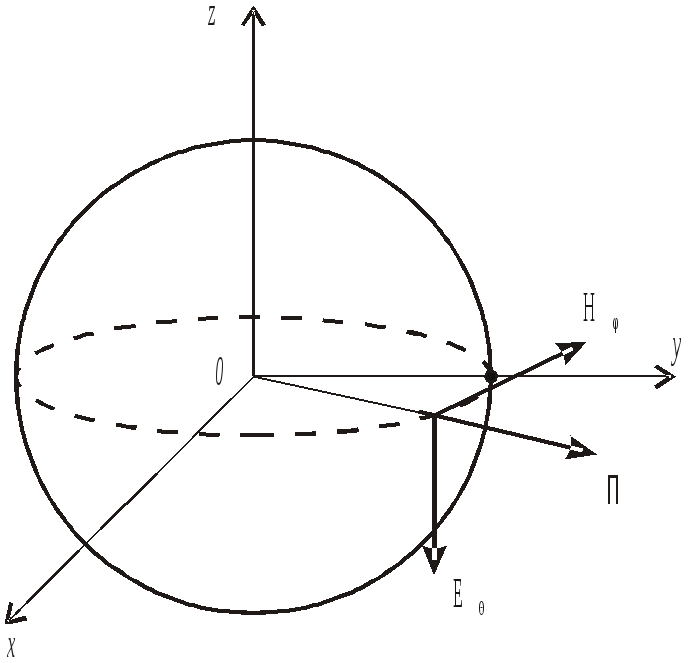и могут быть записаны в следующем виде:
,
,
,
где
- амплитуда колебаний напряженности магнитного поля.






Рис.3.4 Проекции векторов и в ближней зоне




Расположение проекций векторов и в пространстве показано на рис.3.4

Суммарный вектор перпендикулярен вектору и колебания и сдвинуты во времени на 90o.

Мгновенный вектор Пойнтинга в ближней зоне

Как видим, плотность потока мощности электромагнитного поля в ближней зоне излучателя колеблется около нулевого значения, уходя от антенны и возвращаясь обратно. Среднее во времени значение вектора Пойнтинга
.
Итак, в ближней зоне излучения энергии нет.

Особенности ближней зоны

1.Электромагнитная волна не распространяется в пространстве, а колеблется около антенны, причем амплитуды колебаний напряженностей и быстро падают с ростом расстояния r: Hm Em - падает обратно пропорционально r2, а Em – обратно пропорционально r3;

2.Колебания H(t) и E(t) имеет постоянный фазовый сдвиг, равный 90o, в результате чего средняя во времени плотность мощности электромагнитных колебаний равно 0; антенна в ближней зоне эквивалентна реактивному элементу электрической цели (емкости или индуктивности), у которого, как известно, ток и напряжение колеблются в квадратуре.

Ближнюю зону иначе называют зоной индукции.

Дальняя зона

При достаточно больших расстояниях от антенны, где () не учитывать сомножитель в выражениях для , и нельзя. Пренебрегая малыми членами в скобках выражений (2.1), получим
,
,
.
Мгновенные значения напряженностей H и E:
,
,(3.2)
где
,
– амплитуды колебаний напряженностей поля.
Как видим, векторы и перпендикулярны в пространстве и их значения колеблются синфазно во времени. Из (3.2) следует, что выражения для H и E представляют собой волны, бегущие вдоль оси r.

Среднее значение вектора Пойнтинга в дальней зоне
(3.3)
В радиосистемах прием электромагнитных колебаний происходит на расстояниях, существенно больших длины волны, т.е. в дальней зоне.

Особенности дальней зоны

1.Напряженности H и E колеблются синфазно, их амплитуды уменьшаются обратно пропорционально расстоянию r;

2.Плотность мощность электромагнитного поля определяется квадратом амплитуды тока генератора Im, растет с увеличением отношения длины вибратора l к длине излучаемой волны л и падает обратно пропорционально квадрату расстояния;

4.Излучаемая мощность зависит от угла места и и максимальна в направлении, перпендикулярном оси вибратора.

Из выражения (2.3) следует, что для эффективного излучения геометрические размеры антенны должны быть соизмеримы с длиной волны. Этот вывод справедлив для всех антенн.
3.3 Диаграмма направленности антенны
Как видно из (3.1) и (3.3), комплексные амплитуды и плотность мощности электромагнитного поля, излучаемого диполем Герца, зависят от угла места и. Для других антенн эти величины зависят и от азимутального угла ц В общем случае от и и ц зависят амплитуды и фазы и . Поскольку H и E жестко связаны, обычно используют зависимость .

Зависимость амплитуды напряженности электрического поля E в дальней зоне от углов места и и азимута ц при постоянном расстоянии r называется амплитудной диаграммой направленности. Зависимость фазы комплексной амплитуды от и и ц называется фазовой диаграммой направленности.

Зависимость E от и для диполя Герца определяется множителем sinи, поэтому диаграмма направленности имеет вид баранки (тороид вращения) – рис. 3.5




Рис.3.5 Диаграмма направленности диполя Герца




Диаграмму направленности изображают в полярных или декартовых координатах в 2-х плоскостях:

- в плоскости ц = const – рис. 3.6, а;

- в плоскости и = const - рис. 3.6, б.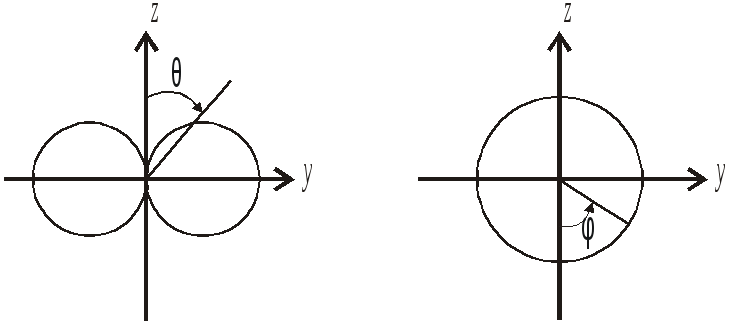




3
Рис.3.6 Диаграмма направленности диполя Герца в 2–х плоскостях

.4 Излучение рамочной антенны
Другим простейшим излучателем является круглая проволочная рамка радиуса a, по которой протекает переменный ток I(t). Допустим, ток меняется во времени по гармоническому закону, т.е.