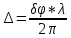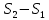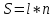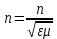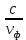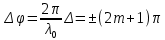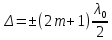Волновая оптика. Квантовая и атомная физика. Элементы квантовой механики.
Гармонические колебания. Механические гармонические колебания.
Гармонические колебания – колебания, при которых физ. величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
x(t)=Asin(ωt+φ)
x(t)=Acos(ωt+φ)
A – амплитуда колебания;
ω(рад/с) – циклическая частота;
φ – начальная фаза колебаний, которая определяет значение полной фазы колебания (и самой величины x) в момент времени t = 0;
(ωt+φ)- полная фаза колебания
Дифференциальное уравнение, описывающее гармонические колебания, имеет вид
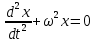
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Вынужденные колебания - совершаются под воздействием внешней периодической силы.
Механическое гармоническое колебание – это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.
x(t)=Asinωt
x(t)=Acosωt
Свободные гармонические колебания в электрическом колебательном контуре.
Электромагнитные колебания – колебания, при которых электрические величины (заряды, токи, электрическое поле, магнитное поле) изменяются периодически.
сопровождаются взаимными превращениями электрического и магнитного поля.
Для возбуждения и поддержания
используются определенные системы.
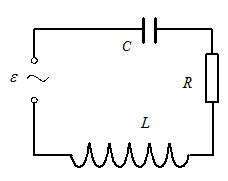
Простейшей такой системой является колебательный контур – цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С, и резистора сопротивлением R.
Свободные электромагнитные колебания — периодически повторяющиеся изменения электрического заряда, силы тока и разности потенциалов, происходящие в колебательном контуре за счет сообщенной этому контуру энергии, которая в дальнейшем не пополняется
Чтобы в контуре возникли
, контур необходимо вывести из состояния равновесия. Для этого зарядим С. Будем полагать, что процессы в контуре происходят достаточно медленно: мгновенные значения тока одинаковы во всех сечениях контура и, следовательно, к контуру применимы законы постоянного тока. В соответствии со 2м правилом Кирхгофа:
Uc=Ec.и.= -L di/dt.
где Uc – мгновенная разность потенциалов на обкладках конденсаторов;
i - мгновенное значение силы тока в колебательном контуре;
Ecи - ЭДС самоиндукции, возникающая в катушке индуктивностью L.
С=q/Uc; Uc=q/C; i=dq/dt;
q/c=-L d2q/dt2; q ̈+ω02q=0
где w0- круговая частота собственных колебаний q на обкладках конденсатора w02=1/ LC
q=q0cos(w0t+φ0)
где q- мгновенное значение заряда обклада конденсатора,
q0- амплитуда колебаний заряда конденсатора.
Сложение гармонических колебаний.
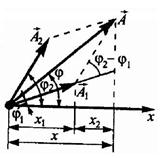
Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс.
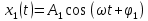
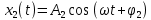
Для сложения колебаний x1 и х2 используем метод вращающегося вектора амплитуды (метод векторных диаграмм).
Так как векторы А1 и A2 вращаются с одинаковой угловой скоростью ω, то разность фаз (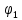 - -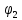 ) между ними остается постоянной. Ур-е результирующего колебания будет ) между ними остается постоянной. Ур-е результирующего колебания будет
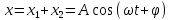
где амплитуда А и начальная фаза 𝜑 задаются соотношениями
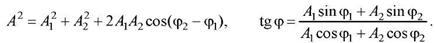
Сумма двух гармонических колебаний одного направления и одинаковой частоты – это гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.
Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:
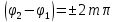 , тогда , тогда 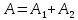
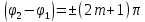 , тогда , тогда 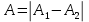
Затухающие колебания.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени.
Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды.
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух):
Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
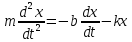
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемом каноническом виде:
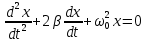
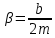 – коэффициент затухания, – коэффициент затухания,
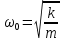 – собственная частота свободных колебаний пружинного маятника. – собственная частота свободных колебаний пружинного маятника.
Вынужденные механические колебания.
Вынужденные колебания – колебания, происходящие под действием внешней переменной силы (вынуждающие силы). Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.
Вынужденные механические колебания - колебания, возникающие под действием внешней периодически изменяющейся силы.
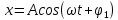 – установившееся вынужденные колебания – установившееся вынужденные колебания
Дифференциальное уравнение вынужденных механических колебаний в каноническом виде:
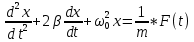
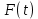 – дополнительная вынужденная сила – дополнительная вынужденная сила
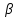 – коэффициент затухания – коэффициент затухания
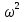 – собственная частота свободных незатухающих колебаний – собственная частота свободных незатухающих колебаний
Амплитуда вынужденных колебанийA и начальная фаза 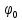 зависят от соотношения частот ω0 (собственная частота свободных колебаний), ω (циклическая частота) и от амплитуды ym внешней силы. зависят от соотношения частот ω0 (собственная частота свободных колебаний), ω (циклическая частота) и от амплитуды ym внешней силы.
Если ω << ω0, то движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом
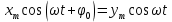
Пружина остается практически недеформированной. Внешняя сила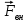 , приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю. , приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю.
Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом.
Зависимость 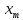 от от 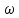 – резонансная характеристика. – резонансная характеристика.
Вынужденные электрические колебания.
Вынужденные колебания – колебания, происходящие под действием внешней переменной силы (вынуждающие силы).
Чтобы вызвать вынужденные колебания нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС.
Дифференциальное уравнение вынужденных колебаний в каноническом виде:
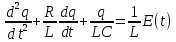
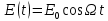
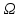 – частота колебаний вынуждающей ЭДС – частота колебаний вынуждающей ЭДС
 Частное решение этого уравнения имеет вид: Частное решение этого уравнения имеет вид:
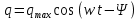
Как и в случае механических колебаний существует электрический резонанс. Амплитуда вынужденных колебаний тока резко возрастает, когда 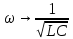 , и достигает максимального значения при , и достигает максимального значения при 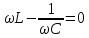
Резонансная частота для силы тока совпадает с собственной частотой контура 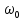 . .
Резонансная частота для заряда и напряжения на конденсаторе равна согласно определению 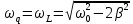 . .
Подставив вместо 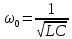 и и 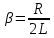 , получим , получим
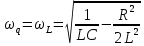 . .
При 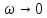 резонансные кривые стремятся к напряжению, возникающему на конденсаторе при подключении его к источнику с ЭДС резонансные кривые стремятся к напряжению, возникающему на конденсаторе при подключении его к источнику с ЭДС
Чем меньше величина 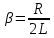 , тем выше и острее получается максимум при резонансе. , тем выше и острее получается максимум при резонансе.
Волновые процессы. Волновое число. Волновое уравнение. Фазовая и групповая скорости. Энергия волны.
Волновой процесс – процесс распространения колебательного движения в сплошной среде.
Волновое число – отношение 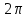 радиан к длине волны: радиан к длине волны:
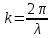 [рад*м-1] = [рад*м-1] = 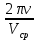 = = 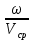
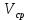 – фазовая скорость волны – фазовая скорость волны
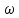 – угловая частота – угловая частота
Волновое число определено для монохроматической волны. К волнам другого вида волновое число относится через преобразование Фурье.
Волновое уравнение в многомерном случае:
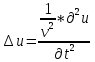
t – время
x – пространственная переменная
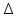 - оператор Лапласа - оператор Лапласа
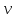 – фазовая скорость – фазовая скорость
u=u(x, t) – неизвестная функция
Волновое уравнение в одномерном случае:
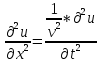
Фазовая скорость – скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления.
Фазовая скорость волны:
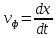
(т.е скорость перемещения)
Групповая скорость – скорость распространения “группы волн”
Для одномерных волн:
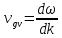
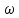 – угловая частота – угловая частота
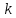 – волновое число – волновое число
Для трехмерного пространства:
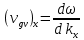
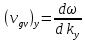
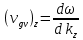
Энергия волны пропорциональна квадрату амплитуды. Скорость переноса энергии равна групповой скорости.
Электромагнитные волны. Основные свойства электромагнитных волн. Энергия электромагнитных волн. Поток энергии. Вектор Умова-Пойнтинга. Излучение диполя.
Электромагнитная волна – распространение в пространстве изменение электромагнитного поля
Основные свойства электромагнитных волн:
Поглощение
Рассеяние
Преломление
Отражение
Интерференция
Дифракция
Поляризация
Полная энергия волны складывается из суммы электрической и магнитной энергии:
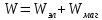
Удобнее представлять энергию через объёмную плотность энергии волны:
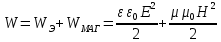
Согласно закону сохранения энергии 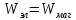 , т.к. векторы E и H колеблются в одной фазе. Поэтому можно записать: , т.к. векторы E и H колеблются в одной фазе. Поэтому можно записать:
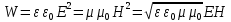
Поток энергии – отношение энергии, переносимой волнами через некоторую поверхность к времени, в течение которого эта энергия переносима
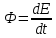
Плотность потока энергии П – векторная величина, равная энергии, переносимой за единицу времени через единичную площадку, 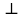 к направлению распространения волны, и совпадающая с направлением фазовой скорости волны. к направлению распространения волны, и совпадающая с направлением фазовой скорости волны. 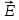 , , 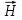 – векторы напряженности электрического и магнитного полей. – векторы напряженности электрического и магнитного полей.
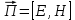 Вектор получил название вектора Умова–Поинтинга. Вектор получил название вектора Умова–Поинтинга.
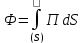
Диполь – 2 равных разноименных точечных заряда +q и -q, находящиеся на некотором расстоянии d друг от друга. Характеризуется дипольным электрическим моментом p:
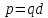
Простейшая излучающая система: линейный гармонический осциллятор – электрический диполь, момент которого изменяется по гармоническому закону:
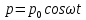
Интерференция света. Когерентные волны. Оптическая и геометрическая разность хода. Условия максимума и минимума при интерференции.
Свет – электромагнитные волны. При их наложении друг на друга должно наблюдаться явление интерференции.
Интерференция – при наложении двух или нескольких волн происходит перераспределение переносимой энергии или энергии между отдельными точками области их наложения.
Условия наблюдения интерференции света:
частоты волн должны быть одинаковыми;
разность фаз колебаний векторов 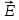 в таких волнах в каждой точке области их наложения должна оставаться постоянной; в таких волнах в каждой точке области их наложения должна оставаться постоянной;
направления, в которых совершаются колебания векторов 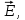 должны совпадать. должны совпадать.
Волны, удовлетворяющие перечисленным условиям – когерентные.
Когерентные волны – волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Оптическая разность хода волн — это разность оптических длин путей, проходимых волнами.
Равна 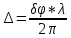
Геометрическая разность хода – разность расстояния от источников волн до точки их интерференции.
Равна разности оптических длин 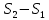
Оптическая длина S – произведение геометрического пути L на показатель преломления среды n
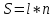
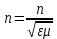 = = 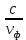
Условие минимума интерференции:
В том случае, если оптическая разность хода будет равна четному числу длин волн в вакууме, то в данной точке наблюдается максимум интенсивности. Условия интерференционного максимума можно записать как:
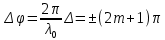
Условие максимума интерференции:
Когда оптическая разность хода равна нечетному числу длин полуволн, то в исследуемой точке наблюдают интерференционный минимум. В виде формулы условие интерференционного минимума записывают:
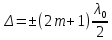
|
 Скачать 384.52 Kb.
Скачать 384.52 Kb.
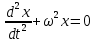

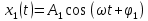
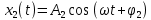
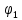 -
-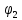 ) между ними остается постоянной. Ур-е результирующего колебания будет
) между ними остается постоянной. Ур-е результирующего колебания будет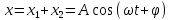
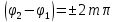 , тогда
, тогда 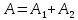
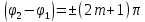 , тогда
, тогда 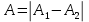
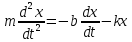
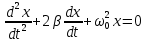
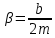 – коэффициент затухания,
– коэффициент затухания, 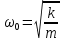 – собственная частота свободных колебаний пружинного маятника.
– собственная частота свободных колебаний пружинного маятника.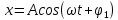 – установившееся вынужденные колебания
– установившееся вынужденные колебания 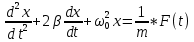
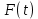 – дополнительная вынужденная сила
– дополнительная вынужденная сила 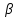 – коэффициент затухания
– коэффициент затухания 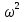 – собственная частота свободных незатухающих колебаний
– собственная частота свободных незатухающих колебаний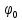 зависят от соотношения частот ω0 (собственная частота свободных колебаний), ω (циклическая частота) и от амплитуды ym внешней силы.
зависят от соотношения частот ω0 (собственная частота свободных колебаний), ω (циклическая частота) и от амплитуды ym внешней силы. 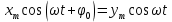
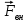 , приложенная к левому концу пружины,
, приложенная к левому концу пружины, 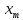 от
от 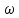 – резонансная характеристика.
– резонансная характеристика.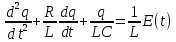
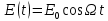
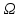

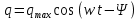
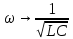 , и достигает максимального значения при
, и достигает максимального значения при 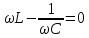
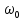 .
.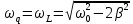 .
.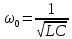 и
и 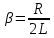 , получим
, получим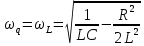 .
.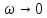 резонансные кривые стремятся к напряжению, возникающему на конденсаторе при подключении его к источнику с ЭДС
резонансные кривые стремятся к напряжению, возникающему на конденсаторе при подключении его к источнику с ЭДС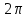
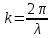
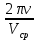 =
= 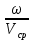
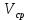
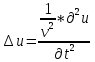
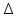 - оператор Лапласа
- оператор Лапласа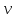 – фазовая скорость
– фазовая скорость 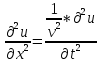
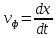
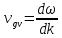
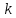 – волновое число
– волновое число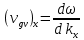
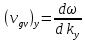
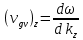
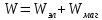
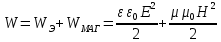
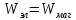 , т.к. векторы E и H колеблются в одной фазе. Поэтому можно записать:
, т.к. векторы E и H колеблются в одной фазе. Поэтому можно записать: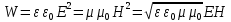
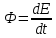
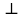 к направлению распространения волны, и совпадающая с направлением фазовой скорости волны.
к направлению распространения волны, и совпадающая с направлением фазовой скорости волны. 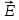 ,
, 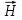 – векторы напряженности электрического и магнитного полей.
– векторы напряженности электрического и магнитного полей. 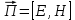 Вектор получил название вектора Умова–Поинтинга.
Вектор получил название вектора Умова–Поинтинга.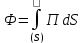
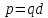
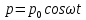
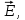 должны совпадать.
должны совпадать.