физика экзамен. Волновая оптика. Квантовая и атомная физика. Элементы квантовой механики
 Скачать 384.52 Kb. Скачать 384.52 Kb.
|
|
Способы наблюдения интерференции света. Опыт Юнга. Вывод формулы для расчета ширины интерференционной полосы. Для получения интерференционной картины необходимы когерентные световые пучки, для формирования которых применяются различные искусственные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов со щелями, зеркал и преломляющих тел (призм). Опыт Юнга можно представить в виде такой схемы. Щели являются источниками O1 и O2 двух когерентных волн. Они расположены на расстоянии d друг от друга. На расстоянии L от щелей помещён экран, причём d должно быть во много раз меньше L. На экране Э наблюдается интерференционная картина в виде чередующихся тёмных и светлых полос, параллельных щелям. В центре картины расположена светлая полоса. Рассмотрим одну из интерференционных полос, расположенную в точке М на экране на расстоянии Z от центра интерференционной картины. Найдём связь Z с параметрами установки. Для этого рассмотрим треугольники O1 M A и O2 M B. Из них находим: 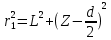 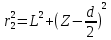 Из второго равенства вычитаем первое: 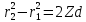 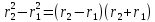 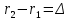 При условии, что 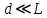 и и 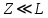 , ,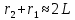 , тогда , тогда 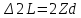 . Отсюда . Отсюда 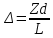 . .Светлая полоса в т. М будет наблюдаться при усл-ии, что 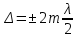 , где m=0, 1, 2… , где m=0, 1, 2…Тогда 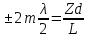 . Отсюда . Отсюда 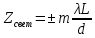 . .Темная полоса в т. М будет наблюдаться при усл-ии 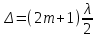 , , Тогда 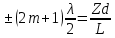 . Отсюда . Отсюда 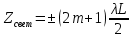 Расстояния между серединами соседних светлых полос равны расстояниям между серединами соседних темных полос 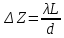 Положение светлых и темных полос и расстояние между ними зависят от длины волны 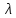 . Если на установку направить белый свет, то в центре интерференционной картины будет наблюдаться белая полоса, а вместо светлых полос – спектры, начинающиеся с фиолетового цвета и заканчивающиеся красным. . Если на установку направить белый свет, то в центре интерференционной картины будет наблюдаться белая полоса, а вместо светлых полос – спектры, начинающиеся с фиолетового цвета и заканчивающиеся красным.Дифракция света. Принцип Гюйгенса. Принцип Гюйгенса-Френеля. Дифракция – огибание волнами препятствий или отверстий, встречающихся на их пути; явление перераспределения световой энергии в пространстве при наложении бесконечно большого числа когерентных волн, в результате чего образуются максимумы и минимумы света. В основу волновой теории света был положен принцип Гюйгенса, который позволял оперировать большим числом когерентных волн. Принцип Гюйгенса формулируется следующим образом: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. Согласно принципу Гюйгенса световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S служит источником вторичной сферической волны. Принцип Гюйгенса: каждая точка фронта волны является источником вторичных когерентных сферических волн. Огибающая этих волн дает положение волнового фронта в последующий момент времени. Если предыдущий фронт волны был сферическим, то и последующий фронт волны будет сферическим. Если предыдущий фронт волны был плоским, то и последующий фронт волны будет плоским. 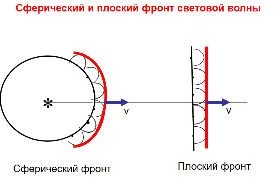 Дифракция вторичных когерентных волн может появиться на резких неоднородностях среды и привести: к огибанию световыми волнами препядствий; захождению света в область геометрической тени. Если эти размеры препядствия соизмеримы с длиной волны света, то дифракция наблюдается в непосредственной близости от препядствия. Если длина волны свет много меньше размеров препядствия, то дифракция становится заметной на расстояниях, значительно превышающих размеры самого препядствия. Принцип Гюйгенса позволял объяснить геометрические законы отражения и преломления света, но не позволял рассчитать интенсивность света в дифракционной картине. Принцип Гюйгенса-Френеля базируется на нескольких предположениях. Действие источника света заменяется действием волновой поверхности (фронта волны): каждый элемент dS этой поверхности является источником вторичных когерентных сферических волн. Элемент поверхности dS гармонически колеблется с амплитудой 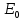 и частотой согласно уравнению: и частотой согласно уравнению: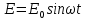 Колебание от элемента dS до точки наблюдения Р на экране пройдет расстояние r и дойдет в виде сферической волны той же частоты, но с уменьшенной амплитудой: 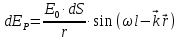 Волны, пришедшие от всех элементов dS волновой поверхности, накладываясь, дают на экране дифракционную картину в виде чередования максимумов и минимумов. Результирующая амплитуда световой волны в точке Р запишется через интегральное суммирование амплитуд волн, пришедших от всех элементов поверхности S. 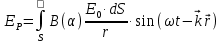 Множители 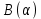 зависят от значения угла зависят от значения угла 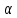 между вектором между вектором 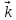 к элементам поверхности dS и радиусом-вектором к элементам поверхности dS и радиусом-вектором 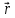 до точки наблюдения Р. до точки наблюдения Р.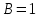 при при 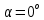 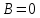 при при 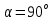 Поскольку вычисление интеграла – сложная задача, Френель предложил геометрический метод сложения амплитуд, названный методом зон Френеля. Зоны Френеля. Пусть S – источник монохроматического света, а P – точка наблюдения света. S и P расположены на одной горизонтальной оси. Разобьём волновую поверхность на зоны (зоны Френеля) так, чтобы расстояние от краёв зоны до точки наблюдения отличались на 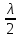 . . Возьмём произвольную точку 1 в первой зоне, тогда во второй зоне найдётся такая соответствующая ей точка 2, что разность хода лучей, идущих в точку P от точек 1 и 2, будет равна 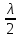 . Вследствие этого колебания точек 1 и 2 погасят друг друга в точке P. . Вследствие этого колебания точек 1 и 2 погасят друг друга в точке P.Из геометрических соображений следует, что при не очень больших номерах зон их площади будут примерно одинаковы. Значит, в каждой точке первой зоны найдётся соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P, уменьшается с ростом номера зоны. Между источником света и экраном нет преград. Полностью открытый фронт волны разделим на зоны Френеля геометрически с помощью циркуля. 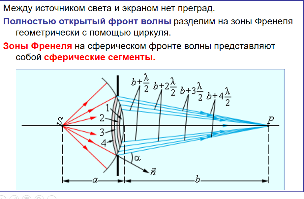 Зоны Френеля на сферическом фронте волны представляют собой сферические сегменты. Зоны Френеля на сферическом фронте волны представляют собой сферические сегменты. 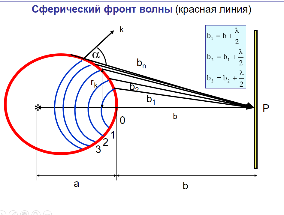 Введем расстояния: a – от источника света до сферического фронта волны; b – от фронта волны до точки Р на экране. На волновой поверхности проведем ряд окружностей радиусами: 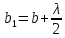 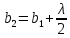 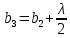 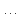 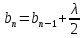 Нумеруем зоны: 0, 1, 2, 3, …, n. Общее число зон (N) велико, практически стремится к бесконечности. Площадь всех зон: одинакова; не зависит от номера зоны. 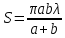 Радиус зон: для сферического фронта волны 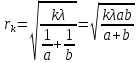 для плоского фронта волны 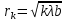 Обозначим амплитуды волн, приходящих в точку экрана Р от каждой последующей зоны, соответственно через 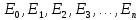 Каждая последующая амплитуда меньше предыдущей за счет увеличения проходимого волной расстояния r и увеличения угла наклона зоны 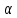 . .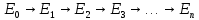 Кроме того, происходит чередование знака амплитуд, т. к.: расстояния, проходимые волнами от краев соседних зон отличаются на 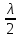 ; ;поэтому в точку Р волны приходят в противофазах. Результирующая амплитуда в точке Р определяется следующей суммой: 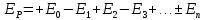 Выражение представляет собой монотонно убывающий знакопеременный ряд, называемый геометрической прогрессией. 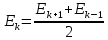 Каждая амплитуда такого ряда определяется как среднее арифметическое двух соседних амплитуд этого ряда. 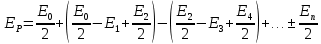 Представим теперь знакопеременный ряд в виде суммы соответствующих «скобок». Все «скобки» равны нулю. 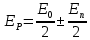 При достаточно большом числе зон амплитуда последней зоны 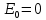 . .Окончательно получим: 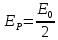 Вывод: результирующая амплитуда от полностью открытого фронта волны равна половине амплитуды волны, пришедшей от центральной зоны Френеля. Рассмотрим два случая: Непрозрачный экран закрывает все зоны, кроме центральной Результирующая амплитуда увеличится в 2 раза: 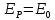 Непрозрачный экран закрывает все нечетные зоны (зонная пластика). Получим еще большее усиление интенсивности света на экране. Условия наблюдения максимумов и минимумов света при дифракции: Максимумы света наблюдаются в тех точках экрана, в которые свет приходит от нечетного числа зон Френеля. Минимумы света наблюдаются, если свет в точку наблюдения приходит от четного числа зон Френеля. Дифракция Френеля от круглого отверстия. Дифракция Френеля от круглого диска. Дифракция от круглого отверстия: Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса. Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия. 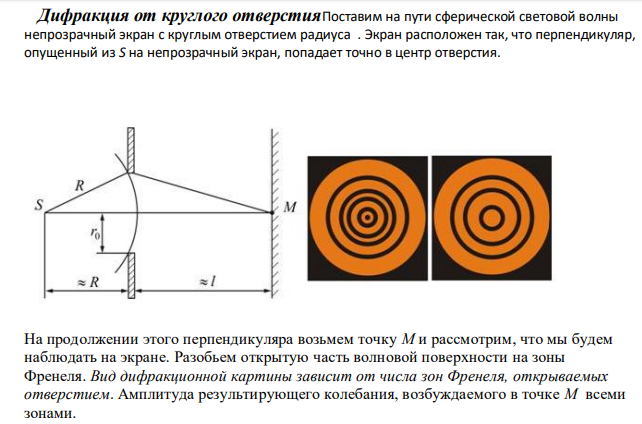 На продолжении этого перпендикуляра возьмем точку М и рассмотрим, что мы будем наблюдать на экране. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами: 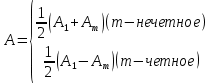 Таким образом: когда отверстие открывает нечетное число зон Френеля, амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; когда отверстие открывает четное число зон Френеля, амплитуда (интенсивность) будет равна 0. Дифракция от диска: Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.  Точка М лежит на перпендикуляре к центру диска. Первая зона Френеля строится от края диска и т. д. Амплитуда световых колебаний в точке М равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке М будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени). Дифракция Фраунгофера от одной щели. Дифракционная решетка. Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием. 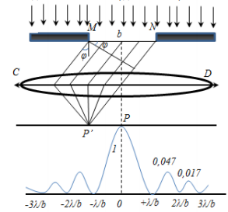 Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели 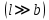 , l – длина, b – ширина. Разность хода между лучами 1 и 2 в направлении ф – , l – длина, b – ширина. Разность хода между лучами 1 и 2 в направлении ф – 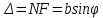 . .Разобьем волновую поверхность на участке щели MN на зоны Френеля, имеющие вид полос, параллельных ребру M щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна 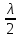 , т.е. всего на ширине щели уложится , т.е. всего на ширине щели уложится 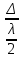 зон. зон.Т.к. свет на щель падает нормально, плоскость щели совпадает с фронтом волны, следовательно все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Число зон Френеля 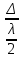 , укладывающихся на ширине щели, зависит от угла , укладывающихся на ширине щели, зависит от угла 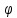 . .Условие минимума при дифракции Френеля: Если число зон Френеля четное, то в точке Р наблюдается дифракционный минимум. Условие максимума при дифракции Френеля: Если число зон Френеля нечетное, то наблюдается дифракционный максимум. Основная часть световой энергии сосредоточена в главном максимуме. Сужение щели приводит к уширению главного максимума и уменьшению его яркости (то же и с другими максимумами). При уширении щели максимумы будут ярче, но дифракционные полосы становятся уже, а число самих полос – больше. При сильном уширении щели в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света. При падении белого света будет разложение на его составляющие. При этом фиолетовый свет будет отклоняться меньше, синий – больше, красный – максимально. Главный максимум в этом случае будет белого цвета. Дифракционная решетка – совокупность большого числа одинаковых, отстоящих друг от друга на одном и том же расстоянии щелей (штрихов, выступов). Существует 2 вида решеток: Отражательные – штрихи нанесены на зеркальную поверхность и наблюдение ведется в отраженном свете. Прозрачные – штрихи нанесены на прозрачную поверхность, наблюдение ведется в проходящем свете. Фронт световой волны разбивается штрихами решетки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах интерферируют друг с другом. Т.к. для разных длин волн максимумы интерференции оказываются под разными углами, то белый свет раскладывается в спектр. 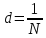 d – период дифракционной решетки N – число штрихов на 1 мм решетки 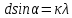 d – период дифракционной решетки 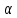 – угол максимума – угол максимумаk – порядок максимума 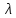 – длина волны – длина волны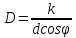 D – угловая дисперсия k – порядок максимума  – длина волны – длина волны |
