|
|
физика экзамен. Волновая оптика. Квантовая и атомная физика. Элементы квантовой механики
Поляризация света. Естественный свет, плоскополяризованный свет, свет поляризованный по кругу, свет эллиптически поляризованный (условия на разность фаз и амплитуды).
Поляризация электромагнитной волны – пространственное соотношение между направлением распространения волны и направлением колебаний ее электрического 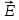 и магнитного и магнитного 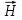 векторов. векторов.
Векторы 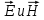 в световой волне колеблются в одинаковых фазах во взаимно перпендикулярных плоскостях, для полного описания состояния поляризации требуется знать поведение лишь одного из них. в световой волне колеблются в одинаковых фазах во взаимно перпендикулярных плоскостях, для полного описания состояния поляризации требуется знать поведение лишь одного из них.
Свет, излучаемый каким – либо источником, представляет собой результат наложения огромного количества световых волн, испускаемых отдельными атомами светящегося тела. Атомы излучают световые волны независимо друг от друга, со всевозможными ориентациями плоскости колебаний. Все направления колебаний равновероятны и амплитуды этих колебаний во всех направлениях одинаковы. Такие световые волны – неполяризованные.
Большинство природных и искусственных источников излучают именно такой неполяризованный свет. Поэтому его называют естественным светом.
Естественный свет – свет, в котором колебание вектора 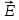 совершаются беспорядочно одновременно во всевозможных направлениях с одинаковой амплитудой. совершаются беспорядочно одновременно во всевозможных направлениях с одинаковой амплитудой.
Плоскополяризованный свет – свет, в котором световой вектор ориентирован только в одном направлении.
Плоскость поляризации – плоскость, совпадающая с направлением светового вектора и направлением распространения света. При сложении двух взаимно перпендикулярных плоскополяризованных световых волн с разными амплитудами и с разностью фаз 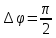 получается эллиптически поляризованный свет. В этом случае конец вектора получается эллиптически поляризованный свет. В этом случае конец вектора 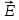 описывает эллипс, лежащий в плоскости, перпендикулярен направлению распространения света. описывает эллипс, лежащий в плоскости, перпендикулярен направлению распространения света.
Еслиамплитуды волн одинаковы 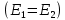 эллипс превращается в окружность. В этом случае поляризация – круговая. эллипс превращается в окружность. В этом случае поляризация – круговая.
Поляризация света. Поляризаторы. Закон Малюса.
Поляризатор – устройство, предназначенное для получения полностью или частично поляризованного оптического излучения из излучения с произвольным состоянием поляризации.
Делятся на: линейные, круговые и эллиптические.
Линейные поляризаторы позволяют получать плоскополяризованный свет.
Круговые – свет, поляризованный по кругу.
Эллиптические – эллиптически поляризованный свет сс заранее определенным типом эллипса.
Применение поляризаторов:
Поляризаторы используются при излучении распределений механических напряжений в прозрачных объектах с помощью поляризованного света, при изучении структуры веществ, широко применяются в фотографических поляризационных светофильтрах и астрономии.
Закон Малюса.
Если два поляроида поставлены на пути лучей так, что их плоскости пропускания параллельны друг другу, то колебания электромагнитного поля световой волны, пропущенные первым из них (поляризатором Р), будут пропущены и вторым (анализатором А). Наоборот, при взаимно перпендикулярном расположении плоскостей пропускания скрещенных поляроидов колебания, пропущенные одним из них, будут задержаны вторым. Таким образом пропускание света парой поляроидов зависит от угла между их плоскостями пропускания.
Амплитудные значения напряженности светового вектора связаны между собой:
ЕА = Ер cos α
А так как интенсивность света I
E2 , то
I = I0 cos2 α
Iо - интенсивность поляризованного света, падающего на анализатор
I - интенсивность поляризованного света, прошедшего через анализатор.
Вторая формула является выражением закона Малюса: интенсивность света I, выходящего из анализатора, пропорциональна квадрату косинуса угла α между направлением плоскостей пропускания вектора Е поляризатора и анализатора.
Для прозрачных поляроидов поляризатор Р пропускает 50% интенсивности естественного света, тогда закон Малюса можно также записать для естественного света
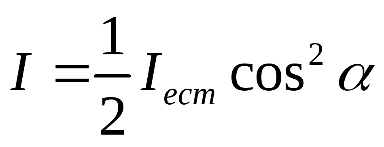
Следствие закона Малюса:
При повороте анализатора интенсивность вышедшего из него поляризованного света будет изменяться от минимального до максимального значения.
Поляризация при отражении и преломлении света на границе двух диэлектриков. Закон Брюстера. Поляризация при двойном лучепреломлении.
Свет, отраженный от гладкой полированной поверхности диэлектрика всегда частично или полностью поляризован.
Пусть на поверхность прозрачного диэлектрика (например, стекла) падает луч естественного света. На границе воздуха с диэлектриком он разделяется на 2 луча – отраженный и преломленный. Отраженный идет обратно в воздух под углом, равному углу падения 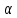 , преломленный распространяется в стекле под углом , преломленный распространяется в стекле под углом 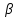 , который связан с углом , который связан с углом 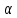 , известным законом преломления , известным законом преломления 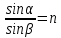
Если угол между отраженным и преломленным лучами прямой, отраженный луч будет полностью поляризован в плоскости, перпендикулярен плоскости падения. Степень поляризации преломленного луча будет при этом максимально, но далеко не полной. Угол падения 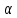 , при котором отраженный луч – полностью поляризованный, называется углом полной поляризации или углом Брюстера. Угол между отраженным и преломленным углом равен 90о , при котором отраженный луч – полностью поляризованный, называется углом полной поляризации или углом Брюстера. Угол между отраженным и преломленным углом равен 90о
Согласно закону преломления: 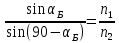 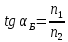
Закон Брюстера: тангенс угла падения при полной поляризации отраженного луча равен относительно показателю преломления. Две среды по отношению к явлению двойного лучепреломления: при распространении света в анизотропных кристаллах световой луч разделяется на 2 луча, поляризованных во взаимно перпендикулярных плоскостях и распространяющихся с различными скоростями.
Особенности явления двойного лучепреломления:
в анизотропных кристаллах существует направление, распространяясь вдоль которого лучи света не испытывают двойного лучепреломления. Это направление – оптическая ось. Главное сечение кристалла – плоскость, проходящая через падающий луч и оптическую, проведенная в месте падения луча.
Анизотропность выражается в том, что физические свойства кристаллов неодинаковы по разным направлениям.
При распространении светового луча вдоль других направлений происходит его разделение на 2 луча, получивших название обыкновенного и необыкновенного.
Обыкновенный луч:
а) лежит в 1 плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения луча.
б) для него отношение синуса угла падения 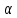 к синусу угла преломления к синусу угла преломления 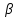 есть величина постоянная: есть величина постоянная: 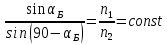 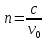
Необыкновенный луч:
а) не лежит в плоскости падения луча. Его направление связано с направлением оптической оси. Он расположен в главном сечении кристалла.
б) отношение 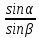 не является постоянной величиной, оно зависит от угла падения луча на кристалл. Это значит, что показатель преломления вещества и скорость распространения не является постоянной величиной, оно зависит от угла падения луча на кристалл. Это значит, что показатель преломления вещества и скорость распространения 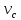 для него в разных направлениях различны и зависят от угла падения луча на кристалл. для него в разных направлениях различны и зависят от угла падения луча на кристалл.
Обыкновенный и необыкновенный лучи полностью поляризованы во взаимно перпендикулярных плоскостях. Двойное лучепреломление наблюдается при падении на кристалл не только естественного, но и линейно поляризованного света. Только интенсивность 2 образовавшихся лучей будет разной в зависимости от угла между плоскостью колебания 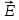 падающего луча и плоскостью главного сечения кристалла. падающего луча и плоскостью главного сечения кристалла.
Тепловое излучение: характеристики теплового излучения, законы теплового излучения абсолютно черного тела (законы Кирхгофа, Стефана-Больцмана, Вина).
Тепловое излучение – электромагнитное излучение, испускаемое телами за счет их внутренней энергии. Излучается телами, имеющими температуру больше 0 К.
Характеристики теплового излучения:
Световой поток Ф – количество энергии, испускаемой поверхностью светящегося тела в единицу времени 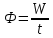
Энергетическая светимость RЭ – количество световой энергии, испускаемой единицей поверхности светящегося тела в единицу времени по всем направлениям 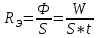
Испускательная способность 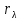 – энергетическая светимость, приходящаяся на единичный интервал длин волн вблизи заданной длины волны – энергетическая светимость, приходящаяся на единичный интервал длин волн вблизи заданной длины волны 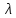 . .
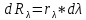 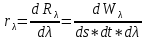 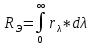
Поглощательная способность 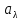 – безмерная величина , показывающая , какая доля от общего количества энергии, переносимой волнами , длины которых заключены в интервале от – безмерная величина , показывающая , какая доля от общего количества энергии, переносимой волнами , длины которых заключены в интервале от 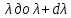 поглатилась телами. поглатилась телами.
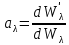 является функцией длины волны и всегда является функцией длины волны и всегда 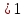
Закон Кирхгофа:
Между испускательной 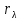 и поглощательной и поглощательной 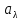 способностями тел существует прямо пропорциональная зависимость, которая выполняется для каждого интервала длин волн в отдельности способностями тел существует прямо пропорциональная зависимость, которая выполняется для каждого интервала длин волн в отдельности
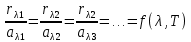
Абсолютно черное тело – тело, имеющее максимальную поглощательную способность, т. е. у которого 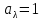 , В природе такого не существует. , В природе такого не существует.
Закон Стефана–Больцмана:
Энергетическая светимость тела (абсолютно черного) прямо пропорциональна четвертой степени абсолютной температуры
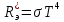
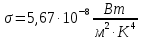 – постоянная Стефана-Больцмана – постоянная Стефана-Больцмана
Закон смещения Вина:
Длина волны, на которую приходится максимум испускательной способности обратно пропорциональна абсолютной температуре.
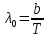
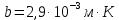 – постоянная Вина – постоянная Вина
Максимальная испускательная способность абсолютно черного тела возрастает пропорционально пятой степени температуры:
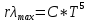
C = 1,29*10-5 Вт/м3*К5
Квантовая гипотеза. Формула Планка. Фотоны. Масса и импульс фотонов.
Квантовая гипотеза – линейные осцилляторы могут колебаться лишь таким образом, что их энергия является целым кратным наименьшего количества энергии 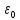
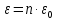
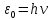 – Квант энергии – Квант энергии
v – частота колебаний
h – постоянная Планка, равная 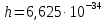 Дж∙с Дж∙с
n = 1,2,3…
Формула Планка: осцилляторы переходят из одного состояния в другое скачком. При этом они излучают или поглощают квант энергии
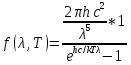
Фотоны – световые кванты, т. е. частицы, в виде которых распространяется свет. Обладает энергией, импульсом, но не обладает массой.
Каждый фотон всегда движется со скоростью света и несет квант энергии. При взаимодействии с веществом фотон передает свою энергию одному или нескольким электронам, после чего фотона больше не существует.
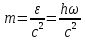
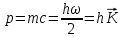
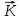 - волновой вектор; его модуль равен волновому числу, а направление совпадает с направлением фазовой скорости световой волны. - волновой вектор; его модуль равен волновому числу, а направление совпадает с направлением фазовой скорости световой волны.
h – постоянная Планка, равная 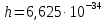 Дж∙с Дж∙с
Фотоэффект. Законы внешнего фотоэффекта. Уравнение Эйнштейна для фотоэффекта. Уравнения для красной границы фотоэффекта. Многофотонный фотоэффект. Применение фотоэффекта.
Фотоэффект – явление испускания электронов веществом под действием света. В твердых и жидких веществах выделяют внешний и внутренний фотоэффект.
Законы внешнего фотоэффекта:
Сила фототока насыщения прямо пропорциональна интенсивности светового излучения (закон Столетова);
Максимальная кинетическая энергия вырываемых светом электронов возрастает с частотой света и не зависит от его интенсивности:
Для каждого вещества при определённом состоянии его поверхности существует граничная частота света, ниже которой фотоэффект не наблюдается. Эта частота и соответствующая длина волны называется красной границей фотоэффекта.
Уравнение Эйнштейна для фотоэффекта:
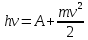
A — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества)
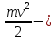 максимальная кинетическая энергия вылетающего электрона максимальная кинетическая энергия вылетающего электрона
Из этой формулы следует существование красной границы фотоэффекта при T = 0 K, то есть существование наименьшей частоты 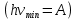 , ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла. , ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла.
Уравнение для красной границы фотоэффекта:
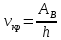 , , 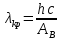
A — т. н. работа выхода
h – постоянная Планка, равная 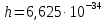 Дж∙с Дж∙с
Многофотонный эффект наблюдается при очень большой интенсивности света,
Электрон, вылетающий из металла, получает энергию от N фотонов (N = 2, 3, 4, 5)
Применение внешнего фотоэффекта:
Кино: воспроизведение звука
Фототелеграф
Измерение силы света, яркости, освещенности
Применение внутреннего фотоэффекта:
Фоторезистор
Фотоэлементы, создающие ЭДС
Давление света. Качественное объяснение давления света на основе электромагнитной теории Максвелла. Опыт Лебедева.
Давление света — давление, которое оказывает световое (и вообще электромагнитное) излучение, падающее на поверхность тела.
Из электромагнитной теории Максвелла следует, что свет, падающий на тело, оказывает на него давление. Достаточно легкое тело можно привести в движение силой светового давления. Сила эта очень мала. Вычисления Максвелла показали, что на Земле солнечный свет давит на 1 м2 черной поверхности, расположенной перпендикулярно лучам с F = 4,5 * 10-6 H.
Величина этого давления для плоской волны, падающей ⊥ поверхности тела, должна быть прямо пропорциональна объемной плотности энергии 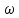 : :
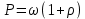
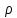 – коэффициент отражения поверхности тела – коэффициент отражения поверхности тела
В 1898 г. русский ученый П.Н. Лебедев с помощью созданной им установки измерил давление света.
Основной частью установки Лебедева бал легкий подвес на тонкой нити с симметрично расположенными «крылышками» (с одной стороны зачерненными, с другой – блестящими). Подвес помещался в сосуд, из которого выкачивался воздух. Свет от дуговой лампы с помощью системы линз и зеркал направлялся на одну из сторон подвеса. Благодаря световому давлению, оказываемому на «крылышки», подвес поворачивался и закручивал нить. Затем свет направлялся на другие «крылышки». С помощью зрительной трубы и зеркальца, прикрепленного к нити, определялся угол закручивания нити. По углу закручивания рассчитывалась величина светового давления. Измеренная Лебедевым величина светового давления в пределах точности эксперимента совпадала со значением, полученным теоретически. Классические опыты Лебедева Явились фундаментальным доказательством электромагнитной природы света.
Эффект Комптона. Особенности эффекта Комптона.
Еще более отчетливо, чем в случае фотоэффекта, квантовый характер взаимодействия света с веществом проявляется в явлении рассеяния рентгеновских лучей.
Опыты Комптона показали, что в рассеянных рентгеновских лучах содержатся как лучи с теми же длинами волн 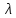 , что и в падающих на рассеивающее вещество , что и в падающих на рассеивающее вещество 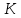 , так и с бОльшими длинами волн , так и с бОльшими длинами волн 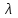 . .
Возрастание длины волны, наблюдаемое при рассеянии рентгеновских лучей, называется эффектом Комптона.
Изменение длины волны 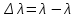 не зависит от длины волны падающего излучения и от материала рассеивающего тела, а зависит только от угла рассеяния не зависит от длины волны падающего излучения и от материала рассеивающего тела, а зависит только от угла рассеяния
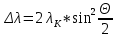
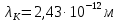 – комптоновская длина волны – постоянная величина, найденная из опыта и равная измерению длины волны при рассеянии излучения под прямым углом – комптоновская длина волны – постоянная величина, найденная из опыта и равная измерению длины волны при рассеянии излучения под прямым углом
Рассеянное излучение обладает высокой интенсивностью для веществ с малым атомным весом и малой интенсивностью для веществ с большим атомным весом.
При увеличении угла рассеяния интенсивность рассеянного излучения в эффекте Комптона возрастает
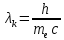 – комптоновская длина волны электрона, равная – комптоновская длина волны электрона, равная 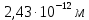
Смещение длины волны рассеянного излучения зависит от угла рассеяния
|
|
|
 Скачать 384.52 Kb.
Скачать 384.52 Kb.