задачи по кинематике с решениями. Учимся решать физические задачи Относительность движения
 Скачать 449.39 Kb. Скачать 449.39 Kb.
|
 Лукина Галина Степановна, автор-составитель Учимся решать физические задачи Относительность движения Нельзя наблюдать и определить движение тела, имеющего конечную величину, не определяя сначала, какое движение имеет каждая его маленькая частичка или точка. Л. ЭЙЛЕР 1. Расчет средней скорости переменного движения В предыдущих номерах журнала уже разбирались некоторые методы и подходы к решению задач по кинематике. Но вступительные экзамены в высшие учебные заведения показали, что задачи на расчет средней скорости неравномерного движения по-прежнему решаются неверно очень многими учащимися. Затруднения вызывают и задачи, в которых решение значительно упрощается переходом в удобную систему отсчета. Поэтому мы еще раз возвращаемся к вопросам кинематики и предлагаем учащимся 9-11 классов внимательно отнестись к предложенным темам.. Итак, движения разделяются:
Равномерное прямолинейное движение – это движение с постоянной скоростью, то есть V = const, a = 0. Обратите внимание, что скорость постоянна и по модулю и по направлению. Переменное движение может быть прямолинейным и криволинейным. Одной из характеристик прямолинейного переменного движения является средняя путевая скорость, которую часто называют просто средней скоростью движения. Для определения средней скорости движения мы истинное сложное движение мысленно заменяем равномерным движением, при котором тот же путь проходится за то же время. 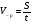 , где S – весь пройденный путь, t – все время движения. , где S – весь пройденный путь, t – все время движения.Обратите внимание, что в физике вводятся два различных понятия средней скорости: векторная средняя скорость, вычисляемая по вектору перемещения тела за определенное время движения Vср = S/t, и скалярная средняя скорость, определяемая длиной пути вдоль траектории, которую мы и называем путевой скоростью. По модулю эти скорости не совпадают, поэтому при решении задач желательно уточнять, о какой средней скорости ведется речь. В приведенных ниже примерах мы будем иметь в виду путевую среднюю скорость. Но иногда в задачах движение задается графиком скорости. Вот тогда уточнение того, о какой средней скорости идет речь, обязательно. Обратите внимание на еще один момент в вычислении средней скорости неравномерного движения. Только в том случае, когда тело движется прямолинейно с постоянным ускорением а, возможно применение формулы Vср = (V1 + V2)/2. Объясняется это тем, 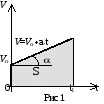 что на графике скорости прямолинейное движение с постоянным ускорением (равнопеременное движение) (рис. 1) может быть представлено линейной зависимостью скорости от времени V = V0 + at что на графике скорости прямолинейное движение с постоянным ускорением (равнопеременное движение) (рис. 1) может быть представлено линейной зависимостью скорости от времени V = V0 + atТак как площадь под графиком скорости численно равна длине пути S за промежуток времени от 0 до t1, то для равноускоренного движения по формуле площади трапеции находим S = (Vо+V)·t1/2. Отсюда сравнением с формулой расчета длины пути S=Vср t1 получаем формулу для расчета средней скорости прямолинейного равнопеременного движения Vср = (V0 + V)/2 или Vср = (V1 + V2)/2, где V1 и V2 соответственно скорости в начале и в конце прямолинейного участка движения. То есть мы фактически заменили данное движение равномерным со скоростью Vср и площадью под линией графика, равной пройденному пути S (рис. 2) 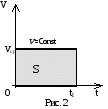 Если же не выполняется хотя бы одно из оговоренных условий: либо движение не прямолинейное, либо скорость зависит от времени не линейно (то есть движение не равнопеременное), применять выведенную выше формулу расчета средней скорости Vср = (V1 + V2)/2 нельзя! В таком случае необходимо пользоваться общей формулой расчета средней скорости Vср = S/t, где S – весь пройденный телом путь, S = S1 + S2 + S3+ S4 + …, t – все время движения, включая остановки; t = t1+ t2+ t3+ t4+… Среднюю скорость можно определять и по графику зависимости пути от времени (рис 3) А В С t ∆t l (t) ∆l Рис. 3 Средняя скорость, равная Vср = Δl / Δt, на этом графике определяется тангенсом угла наклона прямой, соединяющей начальную и конечную точки рассматриваемого участка движения, к оси времени. По этому графику легко можно судить об изменении средней скорости в зависимости от выбора интервала времени. Кроме того, можно определить тот момент времени, когда мгновенная скорость будет по модулю равна средней скорости на заданном участке движения. Для этого нужно параллельным переносом полученного отрезка АВ до касания с линией графика найти точку касания С. Ее координаты и будут соответствовать искомому моменту времени и пройденному к этому моменту времени пути. Задача 1. Первую четверть пути автомобиль двигался со скоростью 30 км/ч, вторую четверть - со скоростью 40 км/ч, а оставшийся путь - со скоростью 80 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
Здесь t1 = 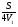 ; t2 = ; t2 = 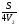 ; t3 = ; t3 = 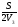 . . Получаем (t1 + t2 + t3) = 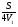 + +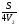 + +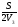 = =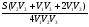 . .Тогда Vср= 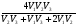 ; Vср= ; Vср=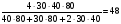 км/ч. км/ч.Ответ: средняя скорость движения автомобиля 48 км/ч. Примечание. Еще раз обратите внимание на расчет средней скорости движения. При неравномерном движении ни в коем случае нельзя рассчитывать среднюю скорость как среднюю арифметическую скорость. Решая подобную задачу, учащиеся часто допускают ошибку, рассчитывая среднюю скорость как 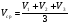 , что совершенно не допустимо! , что совершенно не допустимо!Задача 2. Автомобиль двигался по ровной дороге 1 мин со скоростью 90 км/ч, а затем 2 мин на подъеме со скоростью 60 км/ч и под уклон 0,5 мин со скоростью 120 км/ч. Определить среднюю скорость движения автомобиля за это время.
t S1 S2 S3 V t1 (t1 + t2) (t1 + t2 + t3) Рис. 4 Примечание. 1. Эту задачу можно решать и графически с помощью графика скорости. Для этого необходимо построить в одной системе координат (V, t) графики скорости для каждого интервала времени, затем рассчитать весь пройденный путь как площадь под общим графиком за весь промежуток времени (рис. 4). Средняя скорость может быть найдена отношением всего пройденного пути ко всему промежутку времени 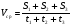 . . Задача 3. Велосипедист проехал первую половину пути со скоростью 12 км/ч, а второю половину пути – со скоростью 20 км/ч. Определить среднюю скорость движения велосипедиста.
Ответ: средняя скорость движения велосипедиста 15 км/ч. Задача 4. Первую половину времени велосипедист двигался со скоростью 12 км/ч, а вторую половину времени – со скоростью 20 км/ч. Определить среднюю скорость велосипедиста за все время движения.
Ответ: средняя скорость движения велосипедиста 16 км/ч. Примечание. Обратите внимание на разницу в условиях задачи № 3 и № 4 и разные значения средней скорости. При этом подход к решению и в том и в другом случаях одинаков. 2. Относительность движения y y/ x x/ 0 0/ Vo Vп Рис. 5 Если тело участвует одновременно в нескольких движениях (например, человек идет по движущемуся вагону, лодка движется по реке и т.д.), то вводятся понятия переносного, относительного и абсолютного движения (рис. 5). За неподвижную систему отсчета чаще всего принимают Землю. Тогда движение подвижной системы отсчета относительно неподвижной (движение вагона относительно земли, движение воды относительно берега) называют переносным движением. Движение тела относительно подвижной системы отсчета (движение человека относительно вагона, движение лодки относительно воды) называют относительным движением. Движение тела относительно неподвижной системы отсчета (движение человека относительно земли, движение лодки относительно берега) называют абсолютным движением. Тогда, согласно механическому принципу относительности Галилея, векторная сумма относительного и переносного перемещения составляет абсолютное перемещение Sп +So =Sa. Векторная сумма относительной и переносной скорости составляет абсолютную скорость Vп +Vo =Va . Векторная сумма относительного и переносного ускорения составляет абсолютное ускорениеa п+ ao = aa. Приведенные выше действия означают переход из одной системы отсчета в другую. Но справедливы они лишь для поступательного движения одной системы отсчета относительно другой (координатные оси движущейся системы отсчета все время параллельны координатным осям неподвижной системы отсчета). Аэропорт Аэропорт Vв Vc Vcв В С Рис. 6 В качестве примера рассмотрим полет самолета в ветреную погоду. Приборы, регистрирующие выбранный летчиком курс, показывают, как расположена ось корпуса самолета по отношению к магнитной стрелке корпуса, а скорость самолета измеряется по обтеканию самолета потоком воздуха. В системе отсчета, связанной с воздухом, скорость самолета будет равна Vo = Vа- Vп или Vс-в = Vс - Vв (рис. 6). Здесь Vс-в – скорость самолета относительно воздуха, Vс – скорость самолета относительно точки на Земле (например, аэродрома), Vв – скорость ветра. Обычно задают направление и скорость ветра (данные метеослужбы), направление на цель и время полета. Этих данных достаточно, чтобы геометрическим образом определить скорость самолета относительно воздуха Задача 5. Эскалатор поднимает неподвижно стоящего на нем пассажира за 1,5 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. За какое время пассажир поднимется по движущемуся эскалатора? За какое время пассажир поднимется по движущемуся эскалатору, если удвоит свою скорость?
Если скорость человека станет V2, то время подъема его по движущемуся эскалатору равно: t4 = l /( Vэ + V2) = l /( l /t1 + 2 l / t2) = t1 t2 / (2 t1 + t2); Подставляя данные величины, получаем : t4 = 0,75 мин = 45 с. Ответ: по движущемуся эскалатору человек поднимается за 1 мин, а при удвоенной скорости за 45 с. Задача 6. Капли дождя в безветренную погоду оставляют на стекле движущегося вагона след под углом 300 к вертикали. Определить скорость падения дождевых капель на землю, если скорость движения вагона составляет 72 км/ч.
Vg Vo Vв Рис. 7 скорость дождевых капель относительно поверхности Земли – абсолютная Va,= Vд. Вектор этой скорости направлен вертикально вниз; скорость дождевых капель относительно вагонного окна – относительнаяVo. Вектор этой скорости является векторной разностью векторов Va и Vп; направлен под углом к вертикали (рис.7). Vo = Va - Vп , или Vo =Vд - Vв. Из получившегося треугольника скоростей находим Vд = Vв Ctg ; Vд = 20 Сtg 300 = 20 1,73 = 34,6 м/с. Ответ: скорость падения дождевых капель равна 34,6 м/с. Решим эту же задачу, взяв в качестве неподвижной системы вагонное окно. Тогда скорость капель в этой системе равна Vo =Vд - Vв. Выполнив векторное вычитание, получаем рис. 7. Дальнейшие действия повторяют предыдущие выкладки и дают тот же результат вычислений. Обращаем внимание на то, что система отсчета в кинематике выбирается исключительно соображениями удобства при математическом описании. Никаких принципиальных преимуществ у одной системы отсчета по сравнению с другой в кинематике нет. Поэтому необходимо научиться уверенно переходить из одной системы отсчета в другую, причем самым рациональным методом, используя векторный характер таких физических величин, как перемещение, скорость, ускорение. Очень важно понимать, что физическая система отсчета и математическая система координат в выбранной системе отсчета совершенно не одно и то же. Так, в системе отсчета, связанной с Землей, координатная система может быть и прямоугольной, и косоугольной, и одномерной, и двухмерной, и трехмерной, с различным направлением координатных осей. При этом следует помнить, что:
Переход в другую систему отсчета сопровождается обязательно вычислением относительных кинематических параметров: перемещения, относительной скорости или относительного ускорения. S1-2 =S1- S2 V1-2 =V1 –V2a 1-2 =a1 – a2. Здесь индекс 1-2 означает параметр первого тела относительно второго, принятого за точку отсчета. Часто переход в другую систему отсчета может сделать ситуацию более наглядной. Например, как узнать, на каком минимальном расстоянии друг от друга пролетят пушечные ядра после одновременного выстрела из двух пушек (рис.8) V2 V1 V2 -V1 V21 l Рис. 8 Для этого достаточно одно из ядер принять за неподвижную точку отсчета (как бы оседлать его). Тогда относительное ускорение второго ядра относительно первого равно a 2-1 =a2 - a1 = g – g = 0. Это значит, что второе ядро относительно первого летит равномерно и прямолинейно со скоростью V2-1= V2 –V1 . Для определения минимального расстояния между ядрами достаточно опустить перпендикуляр из точки отсчета (центр первого ядра) на направление относительной скорости V2-1. Задача 7. По пересекающимся под углом 60 дорогам движутся две автомашины с одинаковыми скоростями 60 км/ч. Через какое время после встречи на перекрестке расстояние между ними будет 30 км?
Решение. 0 SA1 V1 V2 V1-2 A2 Рис. 9 Выберем в качестве неподвижной системы первую автомашину. Тогда скорость второй автомашины относительно первой будет равна V2-1=V2 - V1 (рис. 9). Получившийся треугольник равносторонний. Значит, V2-1=V2 = V1. Время, через которое расстояние между машинами станет S, равно t = S / V2-1. 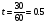 ч = 30 мин. ч = 30 мин.Ответ: через 30 минут расстояние между машинами станет равным 30 км. Задача 8. Под мостом одновременно оказались плот и моторная лодка, плывущие в одном направлении. Обогнав плот, лодка проплыла вниз по реке 16 км и повернула обратно. Проплыв 8 км вверх по течению за 40 мин, лодка встретила тот же плот. Определить скорость течения реки и скорость лодки относительно воды.
реке. Все время движения лодки ( а значит, и плота) равно t = 2t1 . Скорость лодки относительно воды равна 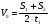 , а скорость плота , а скорость плота 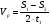 . Подставляя данные, получаем: Vо= 18 км/ч; Vп= 4 км/ч. . Подставляя данные, получаем: Vо= 18 км/ч; Vп= 4 км/ч.Ответ: скорость движения лодки относительно воды 18 км/ч, скорость течения реки 4 км/ч Дано: V1 = 36 км/ч V2 = 54 км/ч L = 2 км ___________ S – ? t - ? Задача 9. Колонна автомашин длиной 2 км движется со скоростью 36 км/ч. Из начала колонны выезжает мотоциклист со скоростью 54 км/ч. Достигнув конца колонны, он возвращается обратно с той же скоростью. Определить, сколько времени мотоциклист был в пути и какой путь прошел, пока снова не нагнал начало колонны? V1 V2 V2 (1) (2) (1) V2 V1 V2-1 (2) V2-1 V1 V2 Рис. 10 Решение.Задачу будем решать в системе, связанной с колонной, которую будем считать неподвижной (рис. 10). Тогда скорость мотоциклиста относительно колонны равна V2-1 = V2 - V1. (Обратите внимание на векторный характер разности!). При движении от начала колонны к ее концу модуль этой скорости равен V2-1= V2 –(- V1 ) = V2 + V1 , а при движении в обратном направлении модуль скорости мотоциклиста равен V2-1= V2 – V1. Тогда время движения мотоциклиста равно t = L/( V2 + V1 ) + L/ (V2 – V1), а пройденное расстояние равно S = V2 t . Подстановка значений в полученные формулы дает результат t = 2/15 ч = 8 мин, S = 7,2 км. Ответ: мотоциклист объехал колонну за 8 минут, пройдя 7,2 км. Примечание. Разобранные выше задачи можно решать, связав систему отсчета с Землей. Но тогда решение будет намного сложнее. Задача 10. На расстоянии 200 м охотничья собака заметила зайца, который убегает со скоростью 40 км/ч. Через сколько времени собака догонит зайца, если она будет бежать со скоростью 60 км/ч? А х 0 Vc В Vз Рис. 11 Дано: V1 = 40 км/ч V2 = 60 км/ч S = 200 м t - ? Решение Задачу удобно решать в системе, связанной с зайцем. Тогда относительно зайца скорость собаки будет равна V2-1 = V2 - V1. По модулю эта скорость равна V2-1 = V2 - V1. Значит, собака догонит зайца через промежуток времени, равный t = S / ( V2 - V1) , то есть через t = 0,01 ч = 36 с. Ответ: собака догонит зайца через 36 с. Задача 11. Спортсмены бегут с постоянной скоростью V на одинаковом расстоянии друг от друга, образуя колонну, длиной l. Навстречу спортсменам бежит тренер со скоростью U < V. Поравнявшись с тренером, каждый спортсмен мгновенно разворачивается и бежит в противоположном направлении со скоростью, равной первоначальной по модулю. Определить длину образовавшейся колонны после разворота последнего спортсмена. Решение. Рассмотрим движение в системе, где тренер неподвижен. Очевидно скорость колонны, движущейся ему навстречу, равна (V + U), а время их встречного движения t1 = l /(V +U). Скорость спортсменов относительно тренера при одинаковом направлении движения равна (V – U). Значит, вновь образовавшаяся длина колонны будет равна L = (V – U) t1, то есть L = (V – U) l /(V +U). Примечание. Попробуйте решить эту задачу в системе, связанной с Землей, и вы убедитесь в нерациональности такого выбора. Разберем решение еще одной задачи в разных системах отсчета. Дано: V1 = 72 км/ч = 20 м/с V2 = 54 км/ч = 15 м/с T = 14 с L - ? Задача 12. Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Определить длину второго поезда. А 1 2 V X/ А 1 2 V X/ l Рис. 12 Решение. Рассмотрим задачу в системе, связанной с наблюдателем А, находящемся в первом вагоне. Тогда скорость второго вагона относительно него равна V2-1 = V2 – V1, по модулю эта скорость равна V2-1 = V2 + V1. Значит, длина второго поезда равна L = V2-1 T = (V2 + V1) T, L = 490 м. Ответ: длина второго поезда равна 490 м. Если же в качестве системы отсчета выбрать Землю, то, выбрав координатную ось Х в направлении движения первого поезда и приняв за точку отсчета начальные координаты наблюдателя А (рис. 13), составляем уравнения движения: А 1 2 V2 X Рис. 13 V1 0 А 1 2 V2 X V1 X1 X2 0 Х1 = V1 T X2 = - V2 T. Длина второго поезда может быть определена разностью Х1 и Х2 L = Х1 - Х2 = V1 T - (-V2 T) = (V2 + V1) T. Результат получился тот же самый. Возможен и графический метод решения задач. Одну из подобных задач мы рассмотрим. Д d B C xo Vr Va ∆l A l α Рис. 14 Д B C Vr Va A α Рис. 15 Vr-a A/ Задача 14. Человек находится в поле на расстоянии 60 м от прямолинейного участка шоссе. Справа от себя он замечает движущийся по шоссе автобус (рис. 14). В каком направлении следует бежать к шоссе, чтобы успеть сесть в автобус? Скорость автобуса VA = 16 м/с, скорость человека VЧ = 4 м/с. Решение Решим задачу в системе, где автобус покоится. Скорость человека относительно автобуса будет равна VЧ-А = VЧ – VА и должна быть направлена на автобус (рис. 15). Отсюда VЧ = VЧ-А + VА Выполнив векторное сложение скоростей в точке А, достроим треугольник скоростей до параллелограмма и проведем окружность радиуса VЧ с центром в точке А'. Тогда Sin α = VЧ / VА.= 0,25 α ≈ 14,50. Ответ: человек должен бежать по направлению, составляющему угол 14,50 с перпендикуляром к шоссе Задача 15. Два мальчика перекидываются мячом, двигаясь одновременно друг к другу. Определить путь, который пролетит мяч за время, в течение которого расстояние между мальчиками сократится с L1 до L2. Скорости мальчиков равны соответственно V1 и V2, скорость мяча Vм. Решение. Выберем систему отсчета, связанную с первым мальчиком. Тогда скорость второго мальчика относительно первого равна V2-1 = V2 – V1, а модуль этой скорости равен V2-1 = V2 + V1. Время перемещения мальчиков друг к другу равно t = (L2 – L1) /( V2 + V1.), а расстояние, которое пролетел мяч за это время S = Vм t.= Vм. (L2 – L1) /( V2 + V1.). Примечание. Чтобы оценить рациональность приведенного метода решения, попробуйте данную задачу решить в системе, связанной с Землей. Задача 16. Автомобиль движется из точки А к перекрестку В со скоростью V1; одновременно второй автомобиль проезжает перекресток и движется к точке С со скоростью V2 (рис. 16). Расстояние АВ = L. Острый угол между дорогами равен α.. В какой момент времени расстояние между автомобилями будет минимальным? Чему равно это расстояние? Решение. При выборе системы отсчета, связанной с Землей, мы не избежим громоздких вычислений. Поэтому такое решение приводить не будем, хотя оно имеет право быть. y x C Д А 0 ВLπ/2lαβVxVy-V1V2V2-1Рис. 16 Решим эту задачу в системе, связанной с первым автомобилем. Тогда скорость второго автомобиля в этой системе равна V2-1 = V2 – V1. В проекциях на координатные оси Vx = -( V2 Соs α + V1); Vу = V2 Sin α . Модуль относительной скорости равен V2-1 = (Vx 2 +Vy2)1/2. Кратчайшее расстояние между автомобилями – перпендикуляр АД = l. Из рис. 16 получаем соотношения: l = L Sin β; ВД = L Соs α; Sin β = Vy/ V; Соs β = Vx / V; t = ВД / V2-1 V2-12 = V22Соs2 α + V12 + 2 V1 V2 Соs α + V22 Sin2 α = V12 +V22 + 2 V1 V2 Соs α Итак, l = LVy /(Vx2 +Vy2)1/2 =LV2Sin α /(V12+V22+2V1V2Соs α)1/2 t = ВД / V2-1 = (L Соs β) / V2-1 = L( V2 Соs α + V1) / (V12 +V22 + 2 V1 V2 Соs α ). Задача 17. При выстреле из двухстороннего пружинного пистолета «снаряды» вылетели в противоположные стороны со скоростями V1 и V2, равными соответственно 2 и 4 м/с. Определить расстояние между ними через 0,1 с, если длина трубки (первоначальное расстояние между «снарядами») равна 10 см. Решение. Свяжем систему отсчета с первым «снарядом», поместив его в начало отсчета. Относительное ускорение второго «снаряда» равно 0, так как оба «снаряда» движутся в гравитационном поле Земли с одинаковыми ускорениями, то есть относительно первого второй движется равномерно со скоростью V2-1 = V2 – V1, по модулю равной V2-1 = V2 + V1; Расстояние через время t равно Х = Х0 + V2-1 t = Х0 + (V2 + V1)t. Х = 0,7 м. Ответ: через 0,1 с от выстрела расстояние между «снарядами» будет равно 70 см. α l B H Vo A y x Рис. 17 Задача 18. Из точки А, находящейся на высоте Н над землей, свободно падает тело, Одновременно с земли из точки В, находящейся на расстоянии l от вертикали падения первого тела, бросают второе тело, так чтобы оба тела столкнулись в воздухе. Определить угол бросания второго тела, если Н/l = 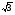 . .Решение. Свяжем систему отсчета с первым телом, свободно падающим из точки А. Так как относительное ускорение второго тела в этой системе равно 0, то скорость его V0 постоянна (рис. 17) и должна быть направлена на точку А (иначе тела не встретятся). Тогда tg α = H /l = 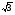 ; α = 600. ; α = 600.Ответ: второе тело должно быть брошено под углом 600 к горизонту. С 0 А ВДу х -V V V V Рис. 18 Задача 19. Найти скорости точек А, В, С, Д колеса, катящегося по земле с постоянной скоростью V без проскальзывания. Решение. Свяжем систему с центром колеса (рис. 18). Тогда скорость точки С равна (-V), скорость точки А равна V, модули скорости всех точек А, В, С, Д равны V. Чтобы найти скорости этих точек относительно Земли, достаточно выполнить векторное сложение относительной скорости и скорости движения центра колеса относительно Земли. Тогда VА = 2 V; V Д = VВ = 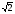 V, VС = 0. V, VС = 0.А 0 В V2 V1 Рис. 19 Задача 20. Две параллельные рейки движутся относительно Земли со скоростями V1 и V2 (V1 > V2) (рис. 19) . Между рейками зажат диск, катящийся по рейкам без проскальзывания. Определить скорость движения его центра. Решение. Свяжем систему отсчета с центром диска. В этой системе отсчета скорости верхней и нижней точек диска одинаковы по модулю, но противоположны по направлению. Поэтому (V1 - V) = - (V2 – V), где V – скорость центра диска. Тогда V = (V1 + V2) /2. Предлагаем решить эту задачу, взяв за систему отсчета нижнюю или верхнюю рейку и сравнить решения и результаты. |

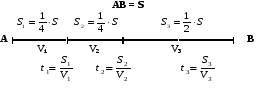
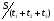 .
.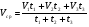 . Подставив данные, получаем
. Подставив данные, получаем 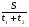 , где t1=
, где t1=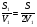 , t2=
, t2=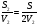 . Тогда (t1+t2)=
. Тогда (t1+t2)=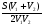 .
. 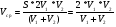 ;
; 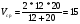 км/ч.
км/ч.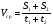 , где
, где 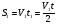 ;
; 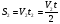 ; t=t1+t2. Тогда S1+S2=
; t=t1+t2. Тогда S1+S2=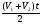
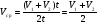 ; Vср=16 км/ч.
; Vср=16 км/ч.