ЛИТЕРАТУРА
1 Артоболевский И.И. Теория механизмов и машин. – М.: Наука. 1988,- 640 с.
2 Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / под ред. И.А.Болотовского. – М.: Машгиз. 1963, - 472 с.
3 Попов Н.К. Курсовое проектирование по теории механизмов и машин.- Минск: Высшая школа. 1995,- 282 с.
4 Смелягин А.И. Теория механизмов и машин. Курсовое проектирование: Учебное пособие. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2003. – 263 с.
5 Теория механизмов и машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др. – М.: Высшая школа, 2003. – 496 с.
6 Ямалтдинов А.И., Щеглов Э.А. Курсовое проектирование по теории механизмов и машин / Учебно-методическое пособие. – Уфа: изд-во УГНТУ. 2006. – 47 с.
|
|
|
|
|
|
Лист
|
|
|
|
|
|
20
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
- на участке замедленного движения фазы приближения (положительная часть графика аналога ускорений на фазе приближения)
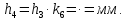
По полученным данным строим график аналога ускорений толкателя в масштабе.
Проводим интегрирование графика аналогов ускорений методом хорд [4], приняв значение полюсного расстояния мм ( H1 = мм). Получаем график аналога скоростей толкателя, который также интегрируем методом хорд для получения графика перемещений. Полюсное расстояние при интегрировании графика аналога скоростей приняли равным мм (H2 = мм).
Рассчитываем масштабы, в которых построены графики движения толкателя:
- масштаб графика перемещений
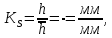
где
h – заданный максимальный ход толкателя,
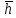 - максимальная ордината на графике перемещений; - максимальная ордината на графике перемещений;
- масштаб графика аналога скоростей
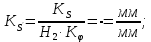
- масштаб графика аналога ускорений
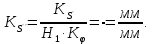
3.2 Определение величины окружности минимального радиуса
Величина окружности минимального радиуса (rmin ) теоретического профиля кулачка для механизма с роликовым толкателем определяется из условия отсутствия заклинивания механизма, т.е. необходимо обеспечить угол передачи движения во всех положениях механизма не меньше заданного минимально допустимого угла передачи γmin = о.
Для определения величины rmin строим диаграмму S – S' в масштабе
Ks = Ks' = мм/мм .
При этом по вертикальной оси откладываем перемещения толкателя в соответствии с графиком перемещений, а по горизонтальной – значения аналогов скоростей для этих же положений. Значения аналогов скоростей на фазе удаления откладываем (т.к. кулачок вращается часовой стрелк ), а на фазе приближения . Соединяем полученные точки плавной кривой и проводим к ней касательные (справа и слева) под углом γmin к горизонтальной оси. Ниже этих прямых сформировалась зона, разрешенная для выбора центра вращения кулачка из условия отсутствия заклинивания при данном минимально допустимом угле передачи движения. Так как задан механизм с внецентренным расположением толкателя (ось толкателя проходит на расстоянии эксцентриситета e от центра вращения кулачка – по заданию e = мм), то откладываем величину эксцентриситета вправо и влево от вертикальной оси (оси S ) в масштабе диаграммы
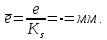
Через полученные отметки проводим вертикальные прямые до разрешенной зоны и обозначаем положение центра вращения кулачка. Выбираем положение центра вращения кулачка, соответствующее меньшему из двух значений rmin (в нашем случае выбираем расположение центра вращения кулачка от оси толкателя). В результате получаем значение 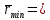 мм на чертеже, что соответствует истинному значению мм на чертеже, что соответствует истинному значению
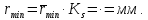
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
18
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
3.3 Построение профиля кулачка
Построение механизма проводим в масштабе K l = мм/мм.
При построении профиля кулачка используем метод обращения движения [1].
Проводим окружность радиусом 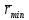 и окружность радиусом и окружность радиусом 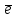 . Делим окружность радиуса . Делим окружность радиуса 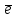 на 12 равных частей, соответствующих 12 положениям механизма, которые он занимает в процессе работы в пределах одного цикла (одного полного оборота кулачка). Нумеруем отмеченные положения в направлении, обратном направлению вращения кулачка. В этих точках проводим прямые, касательные к окружности радиуса на 12 равных частей, соответствующих 12 положениям механизма, которые он занимает в процессе работы в пределах одного цикла (одного полного оборота кулачка). Нумеруем отмеченные положения в направлении, обратном направлению вращения кулачка. В этих точках проводим прямые, касательные к окружности радиуса 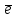 , соблюдая принятое при определении rmin расположение оси толкателя по отношению к центру вращения кулачка – получаем 12 положений толкателя в обращенном движении. Откладываем, в каждом из этих положений толкателя, перемещения в соответствии с графиком перемещений в масштабе K l (перемещения откладываем от окружности минимального радиуса вдоль оси толкателя). Соединив отмеченные точки плавной кривой, получаем теоретический профиль кулачка. Принимаем радиус ролика, равным мм (rрол = мм), что соответствует размеру в масштабе чертежа , соблюдая принятое при определении rmin расположение оси толкателя по отношению к центру вращения кулачка – получаем 12 положений толкателя в обращенном движении. Откладываем, в каждом из этих положений толкателя, перемещения в соответствии с графиком перемещений в масштабе K l (перемещения откладываем от окружности минимального радиуса вдоль оси толкателя). Соединив отмеченные точки плавной кривой, получаем теоретический профиль кулачка. Принимаем радиус ролика, равным мм (rрол = мм), что соответствует размеру в масштабе чертежа
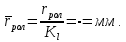
Проводим ряд дуг окружности радиусом 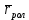 с центром на теоретическом профиле, огибающая к которым (с внутренней стороны теоретического профиля) представляет собой практический профиль кулачка. с центром на теоретическом профиле, огибающая к которым (с внутренней стороны теоретического профиля) представляет собой практический профиль кулачка.
3.4 Определение силы упругости пружины
 Спроектирован кулачковый механизм с силовым замыканием высшей кинематической пары (между кулачком и толкателем). При верхнем расположении толкателя в качестве прижимаю ей силы выступает вес толкателя, но его будет недостаточно для обеспечения постоянного контакта толкателя кулачком в процессе работы механизма, если в некоторых положениях механизма отрывающая толкатель от кулачка сила инерции будет больше веса толкателя. В этом случае необходимо поставить пружину, дополнительно прижимающую толкатель к кулачку. Максимальная отрывающая сила инерции соответствует максимальному отрицательному ускорению толкателя (максимальной отрицательной ординате на графике аналога ускорений). Спроектирован кулачковый механизм с силовым замыканием высшей кинематической пары (между кулачком и толкателем). При верхнем расположении толкателя в качестве прижимаю ей силы выступает вес толкателя, но его будет недостаточно для обеспечения постоянного контакта толкателя кулачком в процессе работы механизма, если в некоторых положениях механизма отрывающая толкатель от кулачка сила инерции будет больше веса толкателя. В этом случае необходимо поставить пружину, дополнительно прижимающую толкатель к кулачку. Максимальная отрывающая сила инерции соответствует максимальному отрицательному ускорению толкателя (максимальной отрицательной ординате на графике аналога ускорений).
Переход от аналога ускорений к ускорениям осуществляется через замену переменных
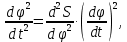
т.е.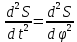
aт = S" . ω12. где
Рисунок 3.2 – Расчетная схема aт – ускорение толкателя,
S" – аналог ускорения толкателя,
ω1 – угловая скорость кулачка.
Таким образом определяем максимальную отрывающую толкатель от кулачка силу инерции:
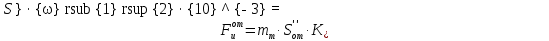
где 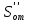 – максимальная отрицательная ордината на графике аналога ускорений в миллиметрах. – максимальная отрицательная ордината на графике аналога ускорений в миллиметрах.
В результате сила упругости пружины, необходимая для силового замыкания, должна быть:
Fуп > Fиот – Gт = Fиот – mт . g = – . 9,8 = Н.
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
19
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
ЛИТЕРАТУРА
1 Артоболевский И.И. Теория механизмов и машин. – М.: Наука. 1988,- 640 с.
2 Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / под ред. И.А.Болотовского. – М.: Машгиз. 1963, - 472 с.
3 Попов Н.К. Курсовое проектирование по теории механизмов и машин.- Минск: Высшая школа. 1995,- 282 с.
4 Смелягин А.И. Теория механизмов и машин. Курсовое проектирование: Учебное пособие. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2003. – 263 с.
5 Теория механизмов и машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др. – М.: Высшая школа, 2003. – 496 с.
6 Ямалтдинов А.И., Щеглов Э.А. Курсовое проектирование по теории механизмов и машин / Учебно-методическое пособие. – Уфа: изд-во УГНТУ. 2006. – 47 с.
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
20
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
- на участке замедленного движения фазы приближения (положительная часть графика аналога ускорений на фазе приближения)
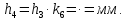
По полученным данным строим график аналога ускорений толкателя в масштабе.
Проводим интегрирование графика аналогов ускорений методом хорд [4], приняв значение полюсного расстояния мм ( H1 = мм). Получаем график аналога скоростей толкателя, который также интегрируем методом хорд для получения графика перемещений. Полюсное расстояние при интегрировании графика аналога скоростей приняли равным мм (H2 = мм).
Рассчитываем масштабы, в которых построены графики движения толкателя:
- масштаб графика перемещений
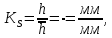
где
h – заданный максимальный ход толкателя,
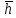 - максимальная ордината на графике перемещений; - максимальная ордината на графике перемещений;
- масштаб графика аналога скоростей
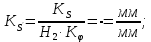
- масштаб графика аналога ускорений
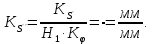
3.2 Определение величины окружности минимального радиуса
Характерной особенностью кулачкового механизма с плоским (тарельчатым) толкателем является невозможность контакта плоской тарелки с вогнутыми участками профиля кулачка. Поэтому в механизме с плоским толкателем величина окружности минимального радиуса определяется из условия выпуклости профиля кулачка во всех его точках, которое описывается формулой Геронимуса Я.Л.:
rmin > - (S + S") .
Для определения значения rmin строим суммарный график (S + S") в едином масштабе K(s+s") Величина rmin выбирается как максимальная отрицательная ордината этого суммарного графика с некоторым конструктивным запасом Δ для избежания заострения профиля кулачка (если суммарный график полностью располагается выше оси абсцисс, то rmin = Δ). В результате построений и данных рекомендаций принимаем 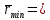 мм в масштабе чертежа суммарного графика, что соответствует истинному значению мм в масштабе чертежа суммарного графика, что соответствует истинному значению
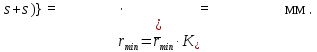
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
18
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
3.3 Построение профиля кулачка
Построение механизма проводим в масштабе K l = мм/мм.
При построении профиля кулачка используем метод обращения движения [1].
Проводим окружность радиусом rmin и делим ее на 12 равных частей, соответствующие 12 положениям механизма, которые он занимает в процессе работы в пределах одного цикла (одного полного оборота кулачка). Нумеруем отмеченные положения в направлении, обратном направлению вращения кулачка. Проводим прямые из центра вращения кулачка через отметки положений на окружности минимального радиуса – получаем 12 положений оси толкателя в обращенном движении. В каждом из этих положений толкателя откладываем перемещения в соответствии с графиком перемещений в масштабе KL (перемещения откладываем от окружности минимального радиуса вдоль оси толкателя). Через полученные точки проводим прямые под заданным углом передачи движения γ= 90 o к соответствующему направлению оси толкателя. Данные прямые показывают положения тарелки толкателя в обращенном движении и формируют замкнутый многоугольник. Проведя огибающую ко всем положениям тарелки толкателя в обращенном движении (вписав в полученный многоугольник плавную кривую), получаем профиль кулачка. В данном случае теоретический и практический профили совпадают.
3.4 Определение силы упругости пружины
Спроектирован кулачковый механизм с силовым замыканием высшей кинематической пары (между кулачком и толкателем). При верхнем расположении толкателя в качестве прижимающей силы выступает вес толкателя, но его будет недостаточно для обеспечения постоянного контакта толкателя с кулачком в процессе работы механизма, если в некоторых положениях механизма отрывающая толкатель от кулачка сила инерции будет больше веса толкателя. В этом случае необходимо поставить пружину, дополнительно прижимающую толкатель к кулачку. Максимальная отрывающая сила инерции соответствует максимальному отрицательному ускорению толкателя (максимальной отрицательной ординате на графике аналога ускорений). Переход от аналога ускорений к ускорениям осуществляется через замену переменных:
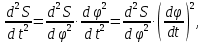
т.е. aт = S" . ω12
где
aт – ускорение толкателя,
S" – аналог ускорения толкателя,
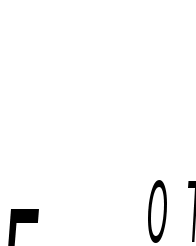 ω1– угловая скорость кулачка ω1– угловая скорость кулачка
Рисунок 3.2 – Расчетная схема .
Таким образом, определяем максимальную отрывающую толкатель от кулачка силу инерции:
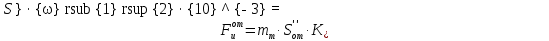
где 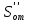 – максимальная отрицательная ордината на графике аналога ускорений в миллиметрах. – максимальная отрицательная ордината на графике аналога ускорений в миллиметрах.
В результате сила упругости пружины, необходимая для силового замыкания, должна быть:
Fуп > Fиот – Gт = Fиот – mт . g = – . 9,8 = Н.
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
19
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
ЛИТЕРАТУРА
1 Артоболевский И.И. Теория механизмов и машин. – М.: Наука. 1988,- 640 с.
2 Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / под ред. И.А.Болотовского. – М.: Машгиз. 1963, - 472 с.
3 Попов Н.К. Курсовое проектирование по теории механизмов и машин.- Минск: Высшая школа. 1995,- 282 с.
4 Смелягин А.И. Теория механизмов и машин. Курсовое проектирование: Учебное пособие. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2003. – 263 с.
5 Теория механизмов и машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др. – М.: Высшая школа, 2003. – 496 с.
6 Ямалтдинов А.И., Щеглов Э.А. Курсовое проектирование по теории механизмов и машин / Учебно-методическое пособие. – Уфа: изд-во УГНТУ. 2006. – 47 с.
|
|
|
|
|
|
|
Лист
|
|
|
|
|
|
20
|
Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
|
 Скачать 138.65 Kb.
Скачать 138.65 Kb.