Курсовая ТОЭ. курсовая тоэ итог. Угловая частота

• Название: Угловая частота
• Анкор: Курсовая ТОЭ
• Дата: 15.06.2021
• Размер: 152.51 Kb.
• Имя файла: курсовая тоэ итог.docx
• Тип: Документы; #217406

R := 5.210³ Ом C := 2.210^{- 9} Ф

Um := 80 В

f := 7010³ Гц

Ψ := 270°

j :=

Угловая частота

ω := 2πf = 4.398 * 10⁵

рад с

1.1. Рассчитайте значение токов на всех элементах цепи, если на входе цепи

действует гармониечеци сигнал:

u(t) := Um*sin(ωt + Ψ)

U :=

_Um jΨ

*e

π


180
= 56.377 + 4.647i

Zc :=

1

jωC

= -1.033i * 10³

Zвх := R + 2Zc = 5.2 * 10³ - 2.067i * 10³

I :=

U

Zвх

= 9.056 * 10^{- 3} + 4.493i * 10^{- 3}

Ur := IR = 47.09 + 23.365i

Uc := IZc = 4.644 - 9.359i

Ur + 2Uc = 56.377 + 4.647i

Si := IU = 0.49 + 0.295i

Sp := I²Zвх Pi := Re(Si)

= 0.49 + 0.295i

= 0.49

Pp := Re(Sp) Qi := Im(Si)

= 0.49

= 0.295

Qp := Im(Sp) = 0.295

Баланс мощностей выполняется

u(t) := Umsin^ωt - Ψ ^{π }


_□ 180 _

100

10
u( t)


50


10
₂ - 4

- 50

2.2 ^{- 4}


10
2.4 ^{- 4}

- 100

t

2. Для заданной цепи получить выражение Рассчитать и построить графики АЧХ и ФЧХ

H (jω) :=

U2(jω)


U1(jω)

H (jw) := ^Uвых =

Uвх

_□ IZc(ω) I(R + 2Zc(ω))

Zc(w) :=
H (w) :=

1

jwC

Zc(w)


R + 2Zc(w)

АЧХ

H( w)
0.4


0.2

0 1 10⁶

2 10⁶

w

3 10⁶

4 10⁶

5 10⁶

ФЧХ

0 1 10⁶

2 10⁶

3 10⁶

4 10⁶

5 10⁶

- 0.5

arg( H( w) )

- 1

- 1.5

w

3 Изобразить в масштабе фрагмент сигнала, если "1" соответсвует +U, а "0" -U Cигнал:

010100

τ1 := 10^{- 3}

T1 := 7τ1

t1 := 0 , 0.00001 .. 1T1

u1(t1) := Um(-Φ(t1) + 2 Φ(t1 - τ1) - 2 Φ(t1 - 2τ1) + 2 Φ(t1 - 3τ1) - 2 Φ(t1 - 4τ

Изображение фрагмента сигнала:



100

- 100

σ(t) := Φ(t)

τ := 10^{- 3}

Выражение для данного сигнала:
U (t) := Um(-σ(t) + 2σ(t - τ) - 2σ(t - 2τ) + 2σ(t - 3τ) - 2σ(t - 4τ) + σ(t -

4. 
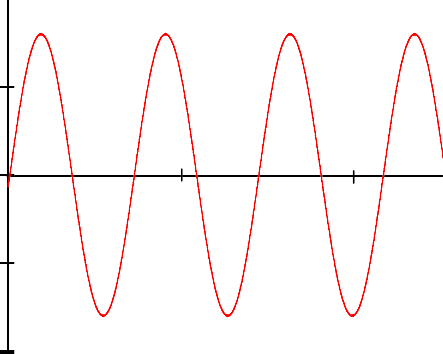
   Найти выражение для спектральной плотности сигнала и построить график модуля этой
   

спектральной плотности
Прямое преобразование Фурье

_∞

^{S(w) :=} 

^- ∞

U(t)e^{- j w t} dt

Выражение спектральной плотности сигнала 010100:

S(ω) := -

1 ₊

jω

2

jω

_e- j ω τ _-

2

jω

_e- j ω 2 τ ₊

2

jω

_e- j ω 3 τ _-

2

jω

_e- j ω 4 τ ₊

j

S1(ω) := UmS(ω)

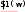
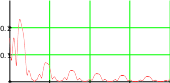
0 1 10⁴

2 10⁴

w

3 10⁴

4 10⁴

4. 
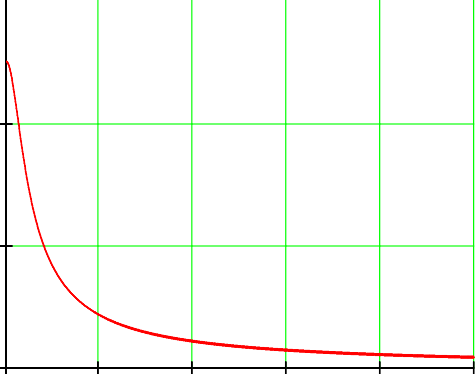
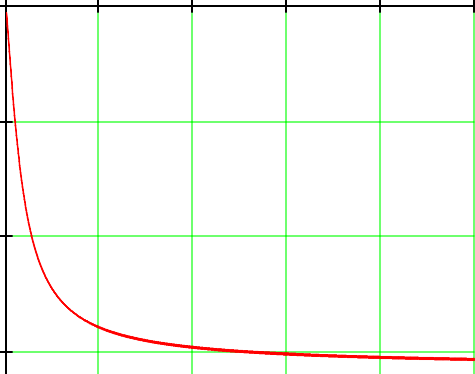
   Рассчитать спектральную плотность сигнала на выходе схемы и построить график модуля
   

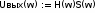этой спектарльтной плотности


10
1.5 ^{- 3}

Uвых( w)

₁ - 3



10

10
₅ - 4

0 1 10⁴
2 10⁴

w

3 10⁴
4 10⁴

6 Найдите выражения для переходной и импульсной характеристик схемы и постройте

графики полученных характеристик Переходная характеристика

1

H (w) :=

j w C

Заменяем jw на

H (p) :=

R + 2
1

1 _p

jwC

RpC + 2
Переходная характеристика g(t) численно совпадает с реакцией цепи на воздействие в виде единичной ступенчатой функции 1(t)

Изображение функции 1(t) =1/p. Операторное выражение реакции цепи U2(p) на воздействие U1(p) = 1/p определяется с использованием операторной передаточной функции по напряжению:

p1 := 0

U2 (p) := U1(p)H(p) =

_□ H(p) p

H(p) _:=

p

1 ₌

p(RpC + 2)

_□ F1(p)

F2(p)

Корни полинома


знаменател
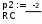я

F2' (p) := 2RC + 2

F2' (p1) := 2

F2' (p2) := -2
g(t) := _ ^{ F1(pk)} e^{pk t} =


_□ F1(p1) _{ep1 t +}


F1(p2) _{ep2 t}

_□ F2'(pk)

k

_□ F2'(p1)

F2' (p2)

Переходная характеристика

- 2 _t

g(t) :=

1 _- 1

2 2

_e R C

График переходной характеристики

g( t)

0.5006

0.5004

0.5002

0.5

0.4998

0.4996

0.4994

0 20 40 60

t

Импульсная характеристика h(t) численно совпадает с реакцие цепи на воздействие в виде

дельта-функции (функция Дирака) δ(t). Изображение функции = 1.

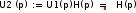Операторное выражение реакции цепи U2(p) на воздействие U1(p) = 1 определяется:

H (p) := ¹ =

RpC + 2

F1(p)



F2(p)

p1 :=

-2

RC

F2' (p2) := RC
h(t) := _ ^{ F1(pk)} e^{pk t} =
_□ F1(p1) _{ep1 t}

_□ F2'(pk)

k

_□ F2'(p1)

Импульсная харакетристика:

- 2 _t

h(t) :=

1

RC

_e R C

График импульсной характеристики
1

h( t)

0.5
0
- 0.5
- 1

- 10 - 5


0 5 10

t

7 На вход заданной цепи подается фрагмент Вашего сигнала. Найдите выражение для сигнала на выходе цепи. Постройте временные диаграммы сигналов на входе и выходе цепи

T1 := 7τ

t := 0 , 0.00001 .. 1T1

Выражение для заданного сигнала на входе цепи
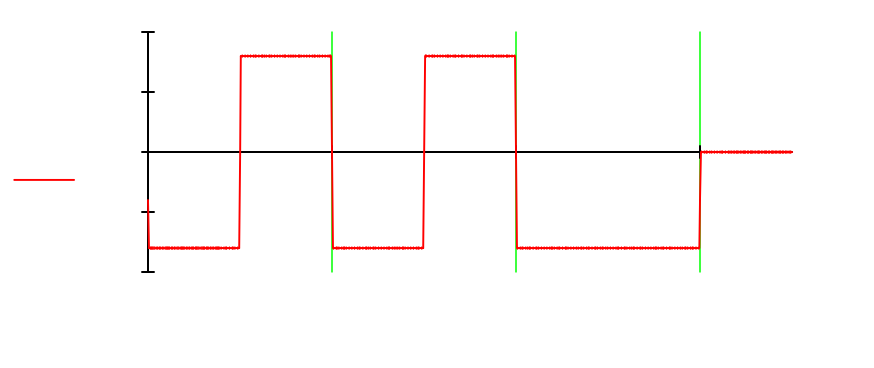
U1 (t) := Um(-Φ(t) + 2Φ(t - τ) - 2Φ(t - 2τ) + 2Φ(t - 3τ) - 2Φ(t - 4τ) + Φ(t

Выражение для заданного сигнала на выходе цепи

U2 (t) := U1(t)g(t)

Диаграмма сигнала на

входе
100

10
U1( t)
50


- 50
- 100
0 2 ^{- 3}

10
₄ - 3

10
₆ - 3

t

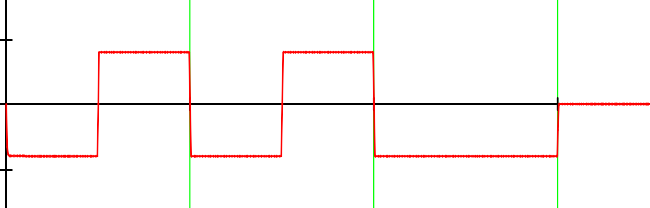
Диаграмма сигнала на выходе

10
U2( t)



50


- 50

0 2 ^{- 3}


6 1

- 3

0

0
4 1 ^{- 3}

t

8. Сделайте обоснованные выводы о возможности использования заданной цепи для передачи Ваших сигналов, если отсчет значения символа сообщения проводится

по уровню +-0.9U в конце каждого символа сигнала

Для данной цепи невозможна передача сигнала, потому что напряжение на конце каждого символа сообщения не достигает уровня +-0.9*U = +-72 В, как видно на Графике, оно не превышает +-50 В.