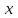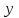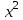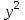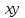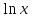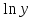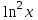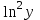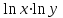Эконометрика_Практическая. Укажите основные этапы эконометрического исследования

• Название: Укажите основные этапы эконометрического исследования
• Дата: 11.12.2022
• Размер: 107.92 Kb.
• Имя файла: Эконометрика_Практическая.docx
• Тип: Документы; #838223

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Эконометрика


Группа
Студент


МОСКВА 2021

ЗАДАНИЕ ПО ПРАКТИЧЕСКОЙ РАБОТЕ

1. 
   Укажите основные этапы эконометрического исследования.
   

Ответ:
I этап (постановочный). Формируется цель исследования, определяется набор участвующих в модели экономических переменных.

При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при этом рекомендуется, чтобы число их было не очень большим и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок, т. е. к явлению мультиколлинеарности.

II этап (априорный). Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации.

III этап(параметризация). Осуществляется непосредственно моделирование, т.е. выбор общего вида модели, выявление входящих в нее связей.

Основная задача, решаемая на этом этапе, — выбор вида функции f(X) в эконометрической модели (1.1), в частности, возможность использования линейной модели как наиболее простой и надежной. От того, насколько удачно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования.

IV этап (информационный). Осуществляется сбор необходимой статистической информации — наблюдаемых значений экономических переменных.

Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия (в условиях активного или пассивного эксперимента).

V этап (идентификация модели). Осуществляется статистический анализ модели и оценка ее параметров.

+С проблемой идентификации модели не следует путать проблему ее идентифицируемости, т. е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений (точнее, параметров структурной формы модели, раскрывающей механизм формирования значений эндогенных переменных, по параметрам приведенной формы модели, в которой эндогенные переменные непосредственно выражаются через предопределенные переменные).

VI этап (верификация модели). Проводится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели, какова точность расчетов по данной модели, в конечном счете, насколько соответствует построенная модель моделируемому реальному экономическому объекту или процессу.

2. 
   Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей.
   

Ответ:
Виды аналитических зависимостей, наиболее часто используемых при построении моделей: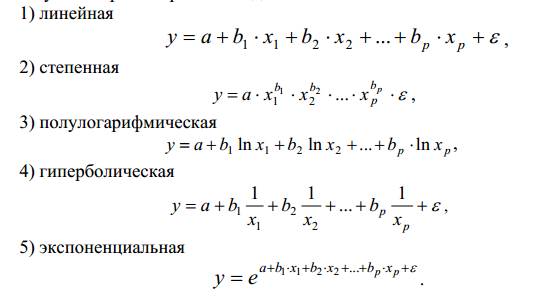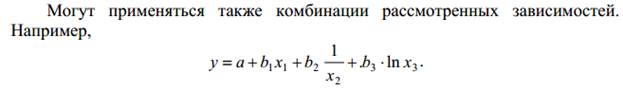

2. 
   Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии.
   

Ответ:

Линейная регрессия:   .
Регрессии, нелинейные по объясняющим переменным:

полиномы разных степеней 

равносторонняя гипербола 

Регрессии, нелинейные по оцениваемым параметрам:

степенная   ;

показательная 

экспоненциальная 

2. 
   Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции r_xy.
   

Ответ:

Выборочный парный коэффициент корреляции ryx: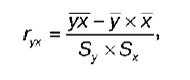



где ух – среднее арифметическое произведения факторной и результативной переменных: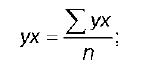



S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной уот ее среднего значения y–: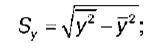



у 2 – среднее значение из квадратов значений результативной переменной у :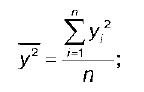

2. 
   Объясните сущность метода анализа динамического ряда.
   

Ответ:
Целью анализа динамических рядов является:

• 
  выявление закономерности изменения изучаемого явления во времени;
  
• 
  прогнозирование (экстраполирование) полученных данных на последующие годы.
  

Задачи:
Задача 1. Рассчитать коэффициенты для различных видов зависимостей.

х	10	20	30	40	50
у	7,38	18,15	44,64	109,79	270,06

Решение.

Линейное уравнение регрессии имеет вид .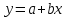

Для оценки параметров используют МНК.

Система нормальных уравнений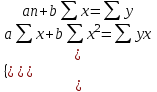

№
1	10	7,38	100	54,4644	73,8
2	20	18,15	400	329,4225	363
3	30	44,64	900	1992,7296	1339,2
4	40	109,79	1600	12053,8441	4391,6
5	50	270,06	2500	72932,4036	13503
Сумма	150	450,02	5500	87362,8642	19670,6

Для наших данных система уравнений имеет вид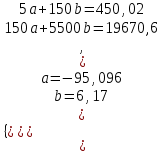

Линейное уравнение регрессии имеет вид .

Степенное уравнение регрессии имеет вид .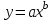

После линеаризации получим: .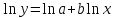

№
1	2,3026	1,9988	5,3019	3,9951	4,6023
2	2,9957	2,8987	8,9744	8,4023	8,6836
3	3,4012	3,7986	11,5681	14,4296	12,9199
4	3,6889	4,6986	13,6078	22,0766	17,3325
5	3,912	5,5986	15,3039	31,3448	21,902
Сумма	16,3004	18,9933	54,7562	80,2484	65,4404

Для наших данных система нормальных уравнений имеет вид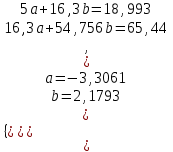

Уравнение регрессии (эмпирическое уравнение регрессии): .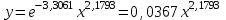

Экспоненциальное уравнение регрессии имеет вид .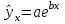

После линеаризации получим: .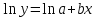

Для расчета параметров регрессии построим расчетную таблицу.

№	x	ln(y)	x2	ln(y)2	x • ln(y)
1	10	1,9988	100	3,9951	19,9877
2	20	2,8987	400	8,4023	57,9734
3	30	3,7986	900	14,4296	113,9589
4	40	4,6986	1600	22,0766	187,9428
5	50	5,5986	2500	31,3448	279,9322
Сумма	150	18,9933	5500	80,2484	659,795

Для наших данных система уравнений имеет вид .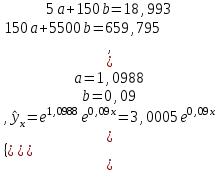

Логарифмическое уравнение регрессии имеет вид .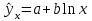

Для расчета параметров регрессии построим расчетную таблицу.

№	ln(x)	y	ln(x)2	y2	ln(x) • y
1	2,3026	7,38	5,3019	54,4644	16,9931
2	2,9957	18,15	8,9744	329,4225	54,3725
3	3,4012	44,64	11,5681	1992,7296	151,8295
4	3,6889	109,79	13,6078	12053,8441	405,0021
5	3,912	270,06	15,3039	72932,4036	1056,4809
Сумма	16,3004	450,02	54,7562	87362,8642	1684,6781

Для наших данных система уравнений имеет вид .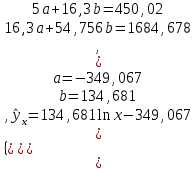
Задача 2. Вычислить коэффициент корреляции для линейной зависимости.

х	10	20	30	40	50
у	7,38	18,15	44,64	109,79	270,06

Решение.

Построим расчетную таблицу.

№
1	10	7,38	100	54,4644	73,8
2	20	18,15	400	329,4225	363
3	30	44,64	900	1992,7296	1339,2
4	40	109,79	1600	12053,8441	4391,6
5	50	270,06	2500	72932,4036	13503
Сумма	150	450,02	5500	87362,8642	19670,6
Среднее	30	90,004	1100	17472,57284	3934,12

Линейный коэффициент корреляции 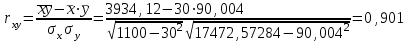, связь между переменными прямая, очень тесная.