матан шпора. Упорядоченность

• Название: Упорядоченность
• Анкор: матан шпора.doc
• Дата: 18.01.2018
• Размер: 1.62 Mb.
• Имя файла: матан шпора.doc
• Тип: Документы; #14460
• страница: 2 из 6

Операции над комплексными числами

Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:

1. 
   Коммутативность сложения: 
   

z1 + z2 = z2 + z1

дlля любых   .

2. 
   Ассоциативность сложения: 
   

(z1 + z2) + z3 = z1 + (z2 + z3)

для любых .

3. 
   Коммутативность умножения: 
   

z1z2 = z2z1

для любых   .

4. 
   Ассоциативность умножения:
   

(z1z2)z3 = z1(z2z3)

для любых   .

5. 
   Дистрибутивность сложения относительно умножения: 
   

z1(z2 + z3) = z1z2 + z1z3

для любых   .

№11. Комплексные числа, операции над ними.

- геометрический смысл

1. Существует элемент i (мнимая единица) такой, что i² = – 1.

2. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b  0) называют чисто мнимыми.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

3. Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

4. Правило сложения и вычитания комплексных чисел.

(a + bi) + (c + di) = (a + c) + (b + d)i.

Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:

(a + bi) – (c + di) = (a – c) + (b – d)i.

5. Правило умножения комплексных чисел.

(a + bi)(c + di) = (aс + bd) + (ad + bc)i.

Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i² = – 1.

Действительно: (a + bi)(c + di) = ac + adi + bdi² = (ac – bd) + (ad + bc)i.

Из второго примера следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:

(a + bi)(a – bi) = a² – abi + abi – b²i² = a² + b².

Произведение двух чисто мнимых чисел – действительное число.

6. Деление комплексного числа a + bi на комплексное число c + di  0 определяется как операция обратная умножению и выполняется по формуле:

.

Формула теряет смысл, если c + di = 0, так как тогда c² + d² = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

№12. Произведение и частное комплексного числа

• 
  Умножение
  

• 
  Деление
  

№13. Модуль и аргумент комплексного числа. Геом. Смысл.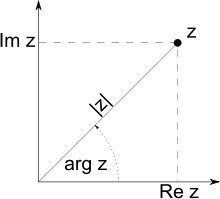


Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа  обозначается  и определяется выражением . Часто обозначается буквами  или . Если  является вещественным числом, то  совпадает с абсолютной величиной этого вещественного числа.

Для любых  имеют место следующие свойства модуля. :

1) , причём  тогда и только тогда, когда ;;

2)  (неравенство треугольника);

3) ;

4) .

Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .

5) Для пары комплексных чисел  и  модуль их разности  равен расстоянию между соответствующими точками комплексной плоскости.

Угол  (в радианах) радиус-вектора точки, соответствующей числу , называется аргументом числа  и обозначается .

Из этого определения следует, что ; ; .

Для комплексного нуля значение аргумента не определено, для ненулевого числа  аргумент определяется с точностью до , где  — любое целое число.

Главным значением аргумента называется такое значение , что . Часто главное значение обозначается ^[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: .

№14. Тригонометрическая и показательная формы

Если вещественную  и мнимую  части комплексного числа выразить через модуль  и аргумент  (, ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме



Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где  — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

№15. Формула Муавра и извлечение корней из комплексных чисел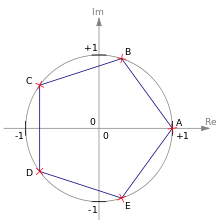

Корни пятой степени из единицы(вершины пятиугольника)

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:



где  — модуль, а  — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней -ой степени из ненулевого комплексного числа: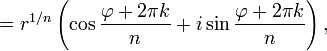







Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса  с центром в начале координат (см. рисунок).

№16. извлечение корней n-ной степени комплексных чисел



Вапв

Вап

Ва

№17. . Алгебраические уравнения, теорема Гаусса.

Алгебраическое уравнение — уравнение, получающееся при приравнивании двух алгебраических выражений.

Алгебраическое выражение — выражение, составленное из букв. Чисел, скобок, соединенных знаками алгебраических операций: +, -, *, :, возведение в степень, извлечение корня.

Примеры алгебраических уравнений:

X²+XY+Y²-X+1=0 ;   =2

 Алгебраическое уравнение с одним неизвестным может быть преобразовано к виду (1):

a₀ + a₁x + a₂x² + …+ a_nxⁿ = 0

Способы решения таких уравнений первой и второй степени известно еще из древности. В XVI в. были найдены способы решения уравнений третьей и четвертой степени.

Основная теорема алгебры (теорема Гаусса).

Любое алгебраическое уравнение (1) степени N имеет N решений (корней) действительных или мнимых, если каждый корень считать столько раз, какова его кратность.

Корень многочлена  a₀+ a₁x + a₂x²+ …+ a_nxⁿ  (a_n0) — это число z₀, такое, что:

a₀ + a₁ z + a₂ z² + …+ a_n zⁿ = 0

Свойство корня:

Число z₀ — корень (1)  многочлен (1) можно представить в виде

 

(x - z₀) (b₀+ b₁x + b₂x²+ …+ b_n-1x^n-1),

 то есть (1) делится на (x-z₀)  без остатка.

Если  (1) делится на (x-z₀)^k, но не делится на (x-z₀)^k+1, то z₀ называется корнем кратности k, при этом

(x-z₀)^k(b₀+ b₁x + b₂x²+ …+ b_n-kx^n-k).

Доказано, что решения уравнений степени выше четвёртой нельзя выразить через коэффициенты уравнения при помощи алгебраических действий.