|
|
матан шпора. Упорядоченность

Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2.Если функцииf(x) и g(x) имеют пределы в точке, то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых,т.е.
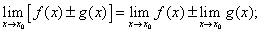 (2) (2)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
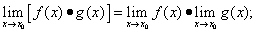 (3) (3)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю,т.е.
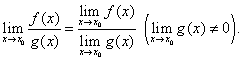 (4) (4)
Замечание.Формулы (2) и (3) справедливы для любого конечного числа функций.
Следствие 1.Предел постоянной равен самой постоянной, т.е.
Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функцияf(u) непрерывна в точке, то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
№35.Первый замечательный предел
I. 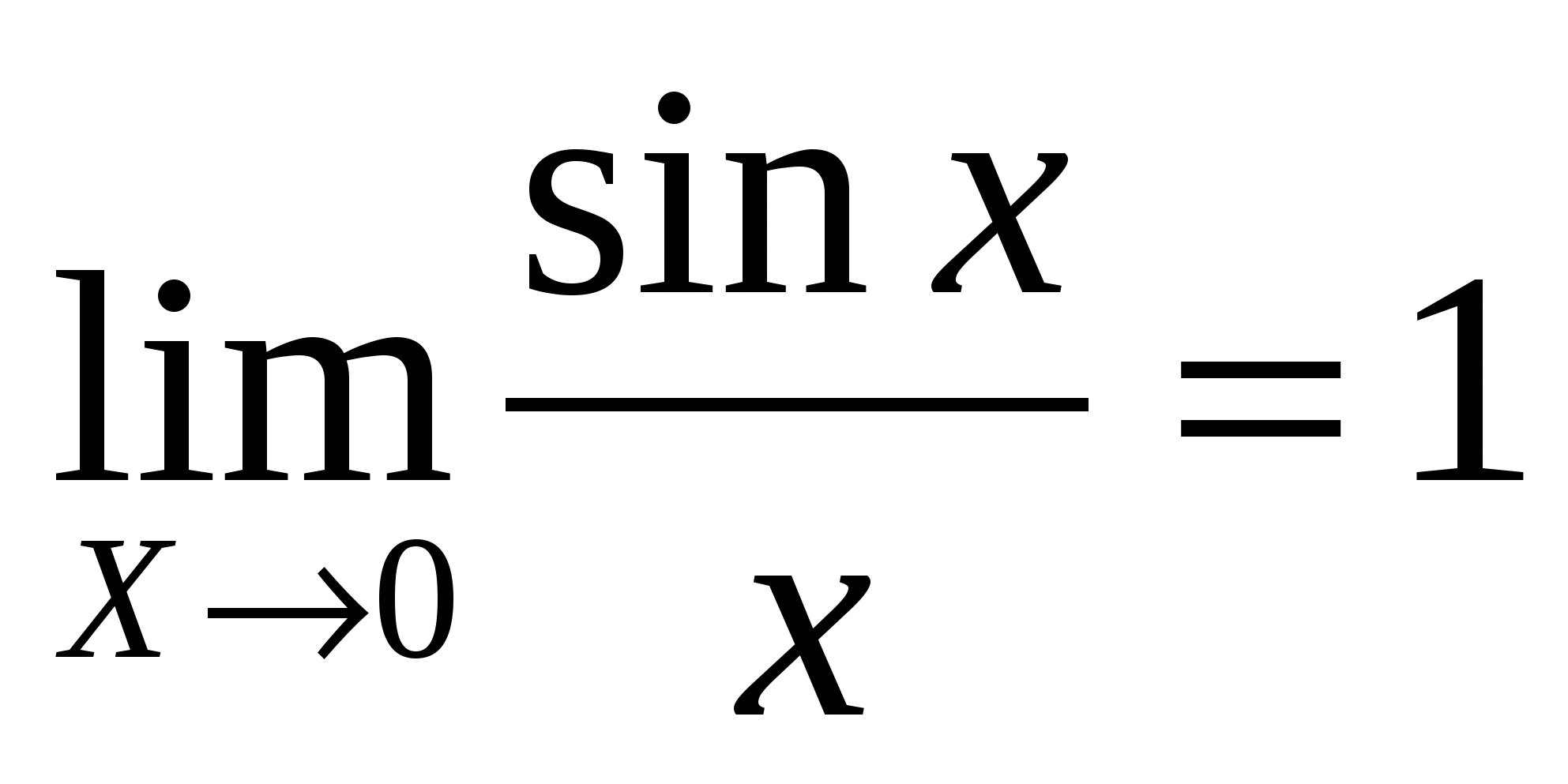
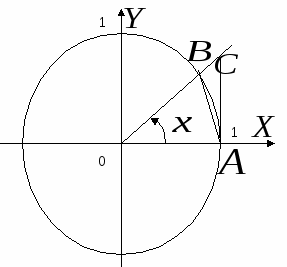
Функция 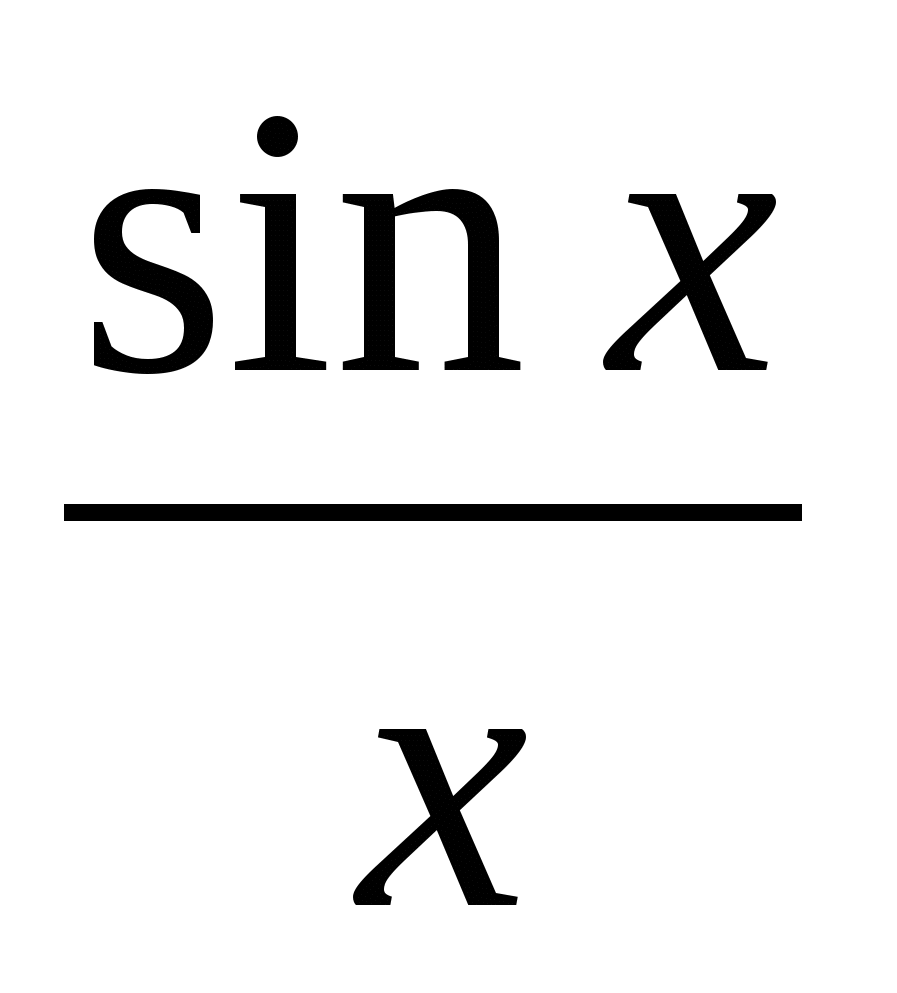 – четная, поэтому можно ограничится только положительными значениями – четная, поэтому можно ограничится только положительными значениями 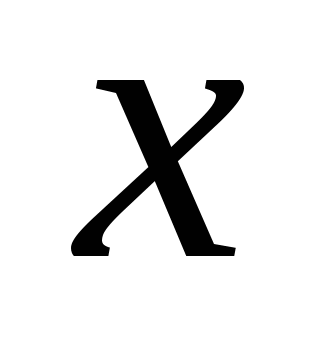 и т. к. и т. к.  , то можно ограничится значениями , то можно ограничится значениями 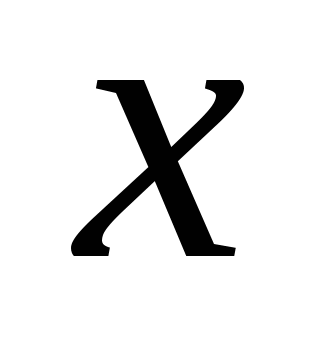 в первой четверти, т. е. в первой четверти, т. е. 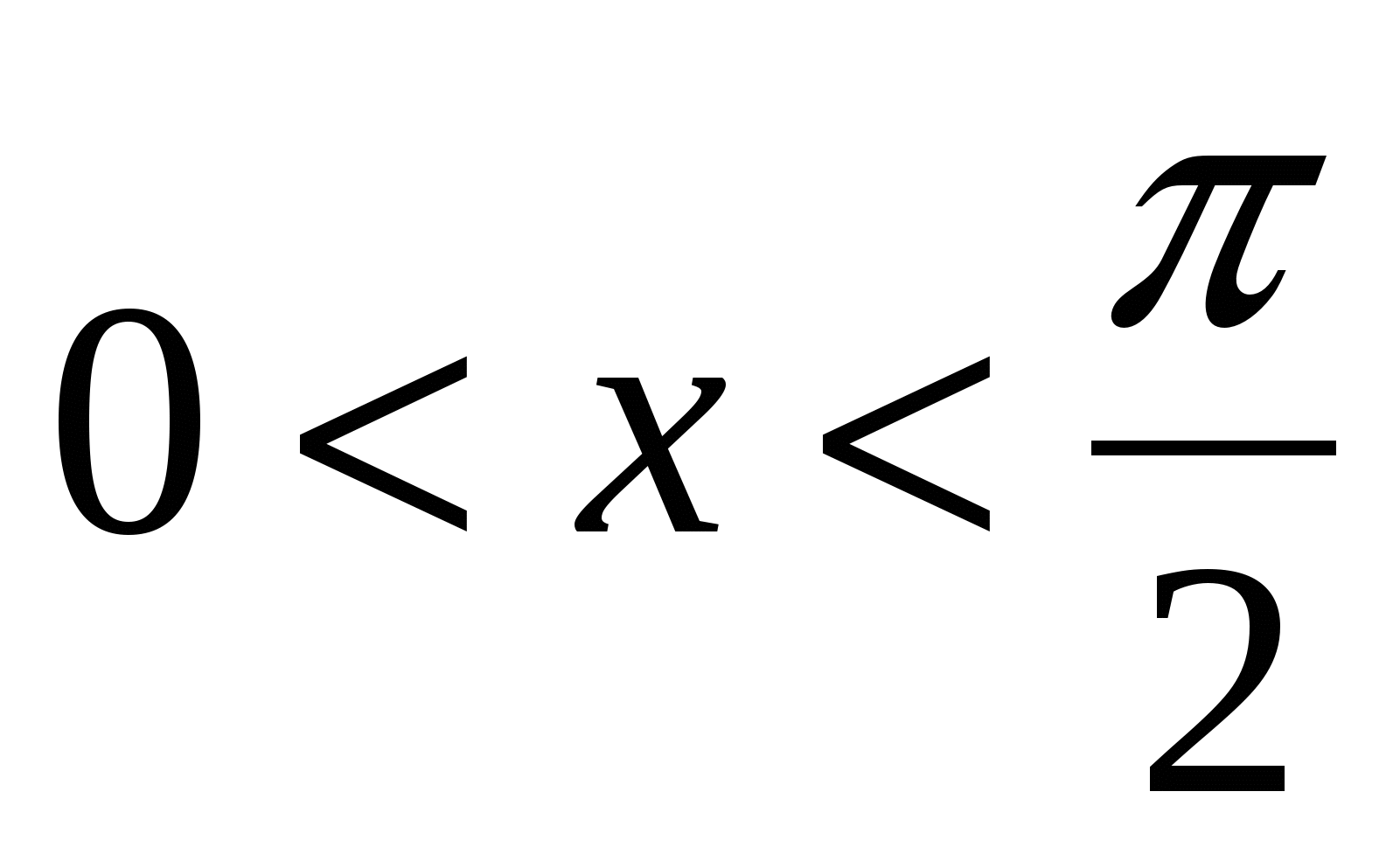 . Рассмотрим площади трех фигур: . Рассмотрим площади трех фигур:
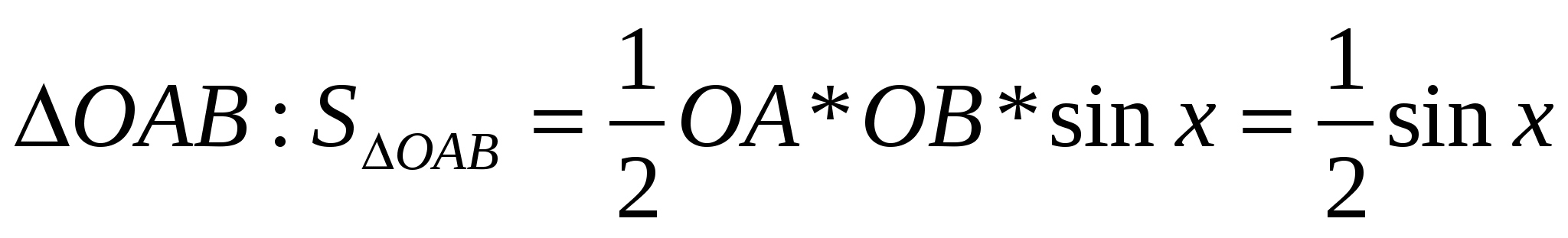 . .
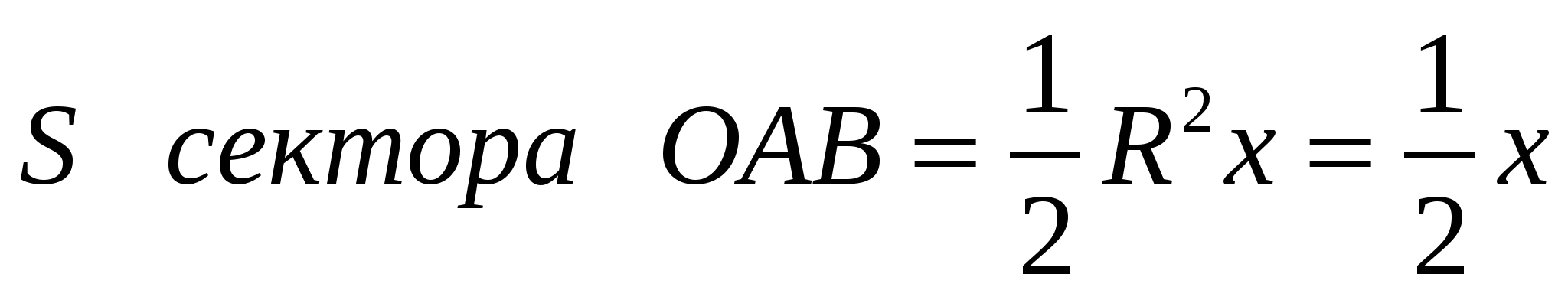 . .
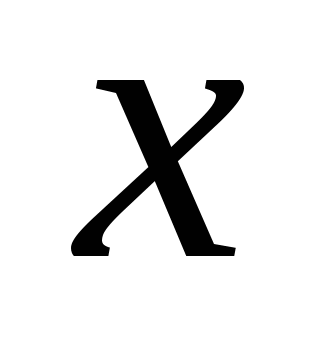 – радианная мера угла. – радианная мера угла.
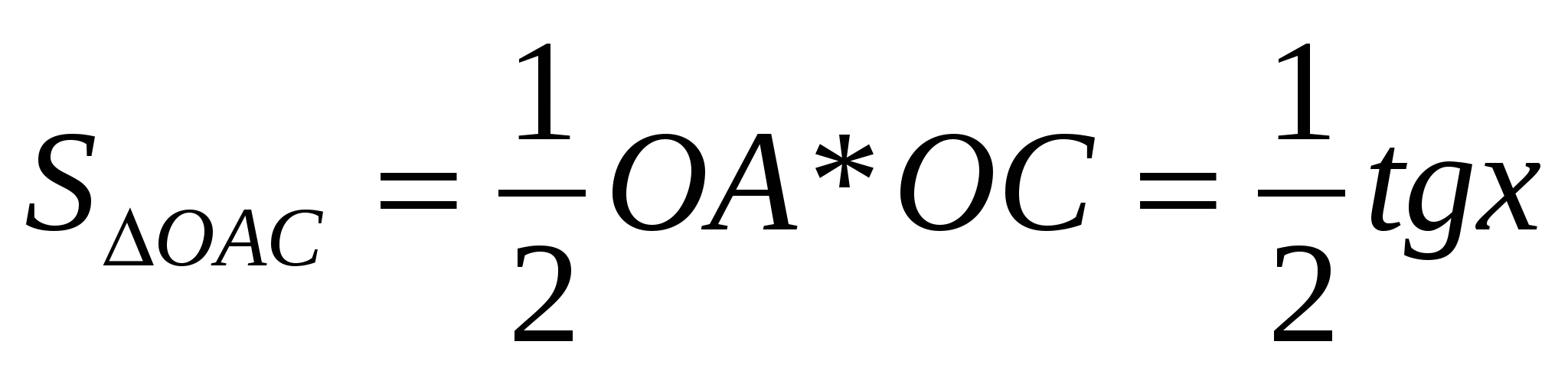
№36. Второй замечательный предел.
ОПРЕДЕЛЕНИЯ:
Переменная 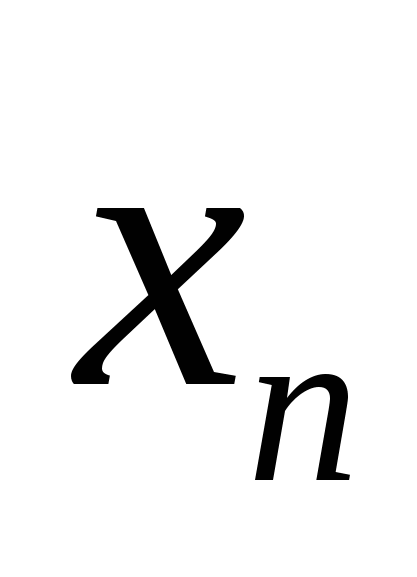 называется возрастающей в узком смысле (строго возрастает), если при называется возрастающей в узком смысле (строго возрастает), если при 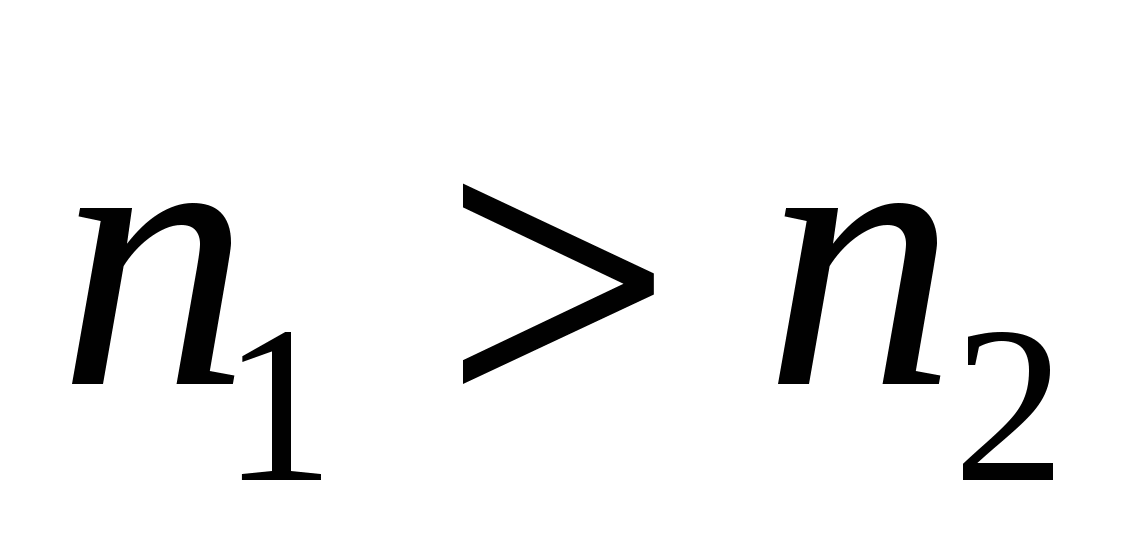 следует следует 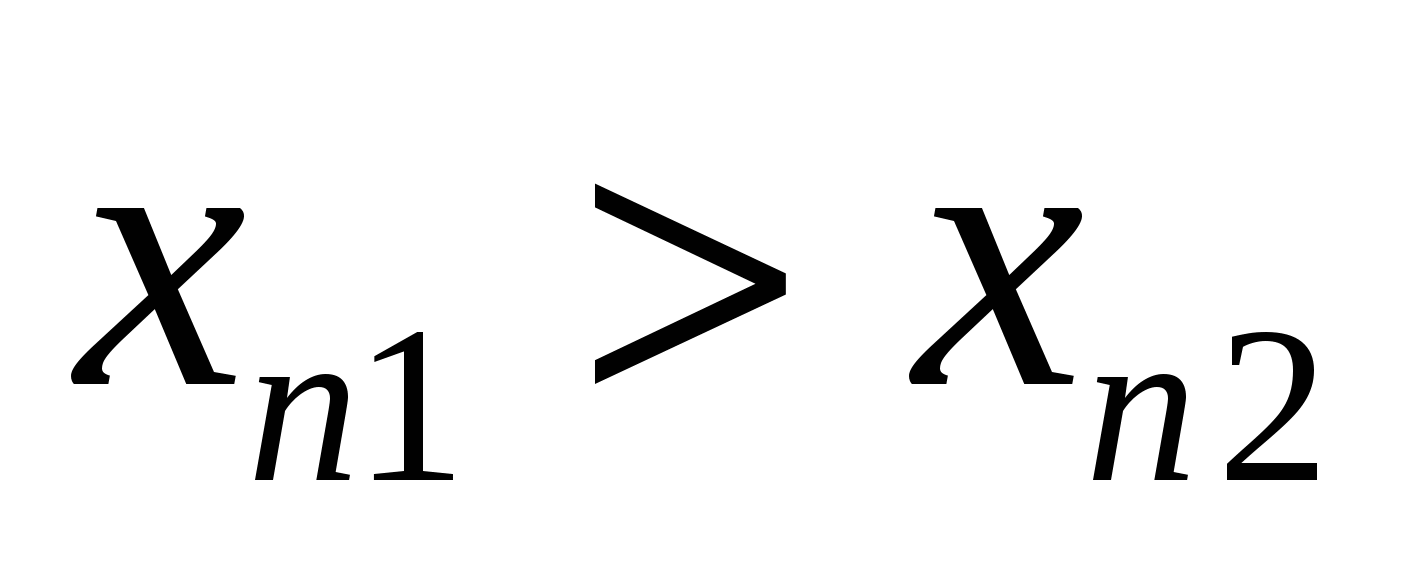 . .
Переменная 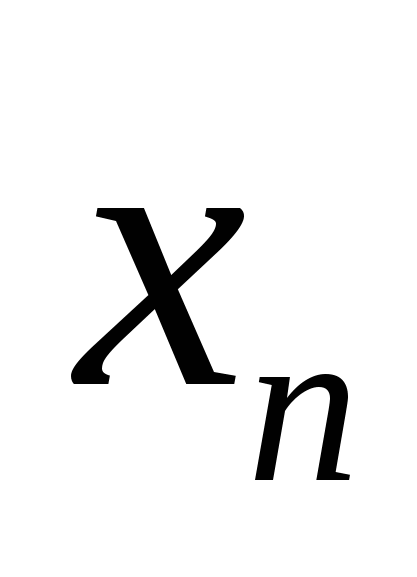 называется строго убывающей, если при называется строго убывающей, если при 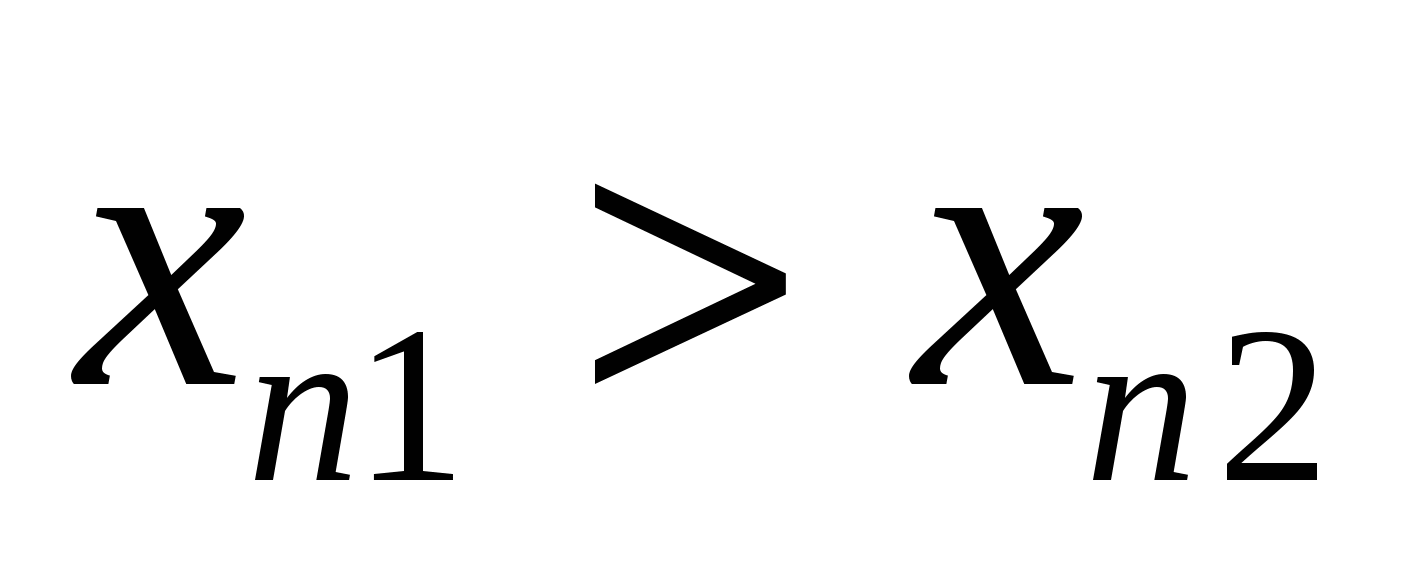 следует следует 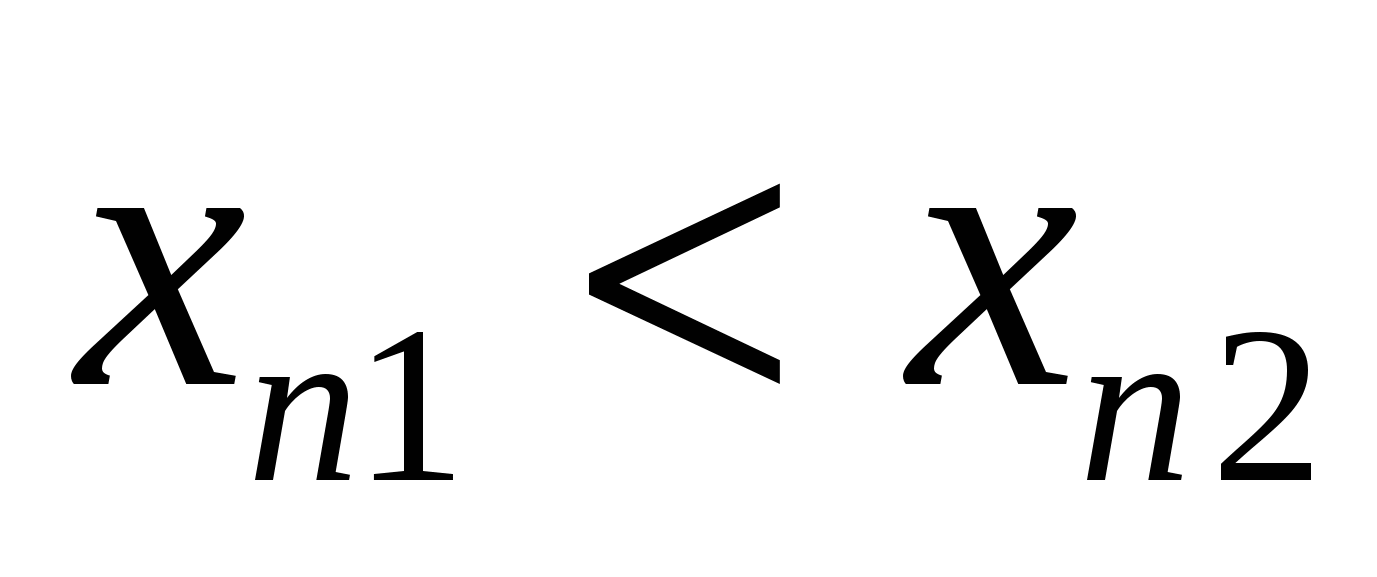 . .
Переменная 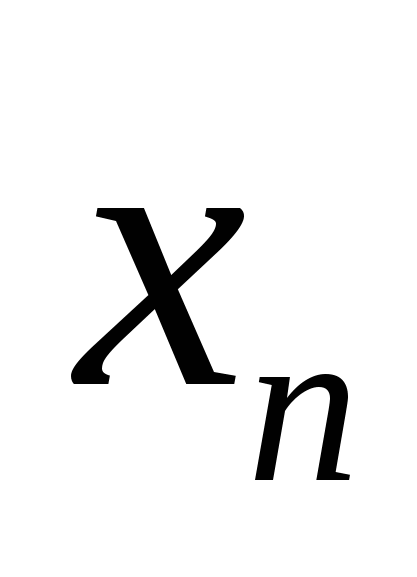 называется возрастающей в широком смысле, иначе не убывающей, если при называется возрастающей в широком смысле, иначе не убывающей, если при 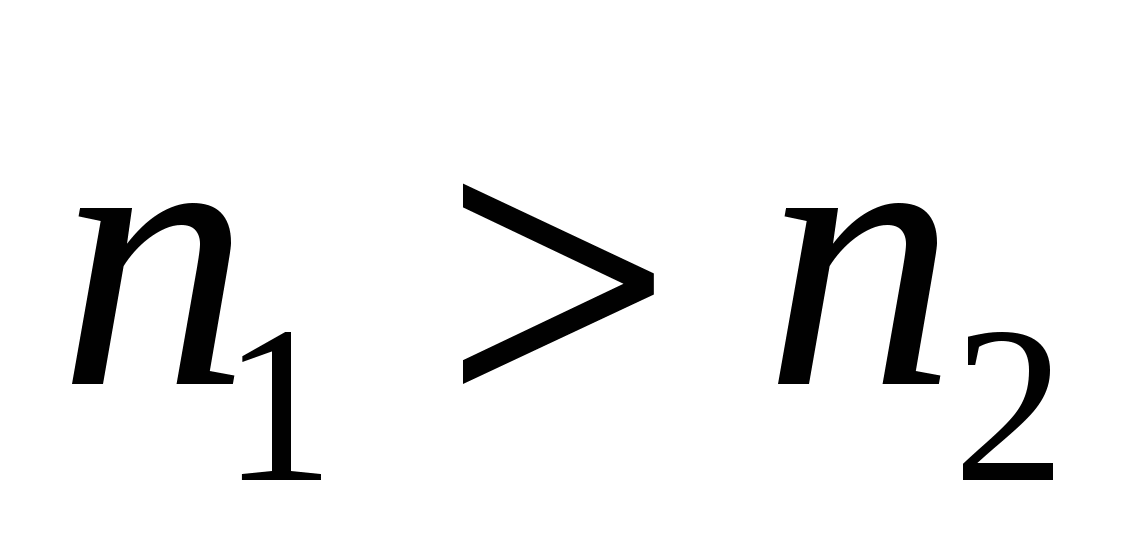 следует следует 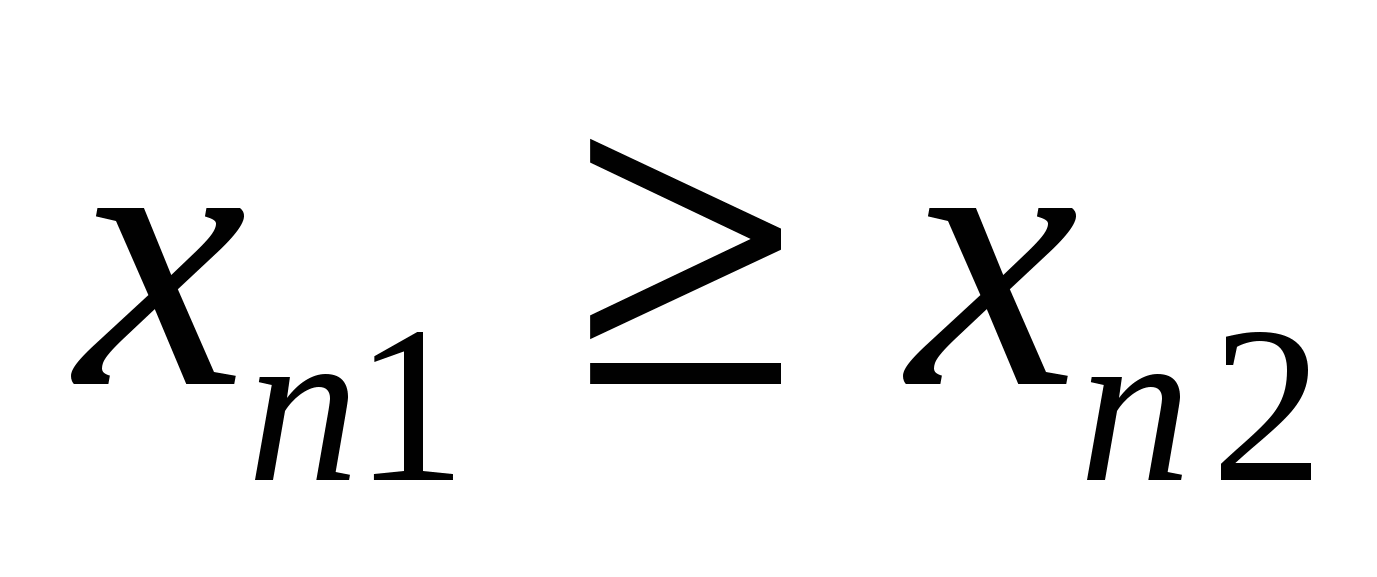 . .
Переменная 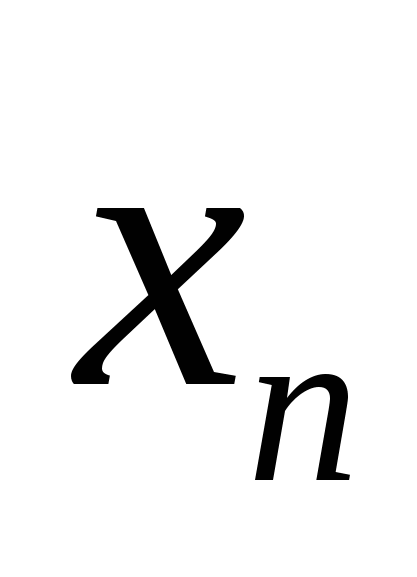 называется возрастающей в широком смысле, иначе не убывающей, если при называется возрастающей в широком смысле, иначе не убывающей, если при 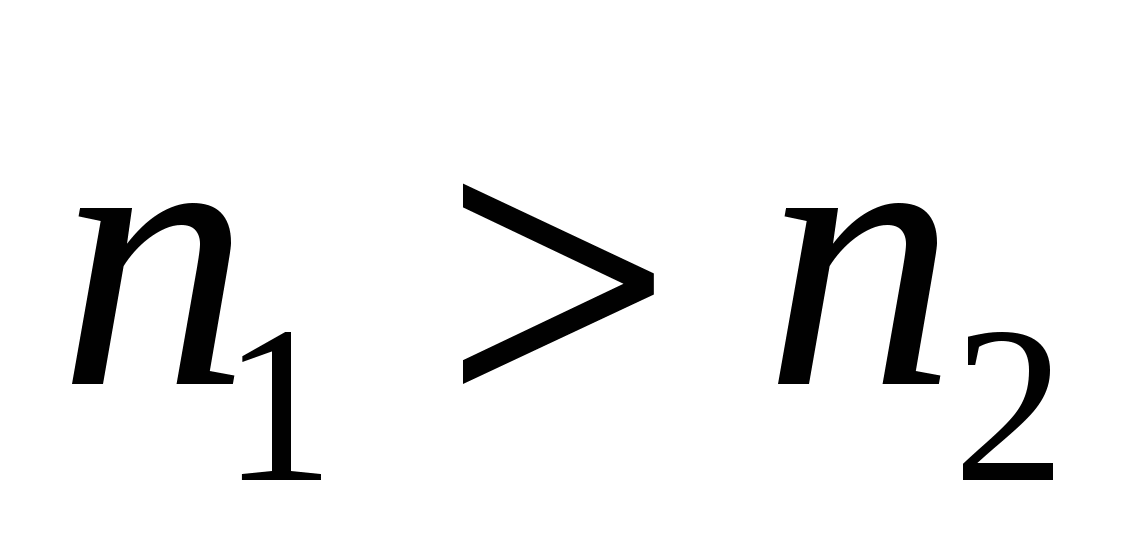 следует следует 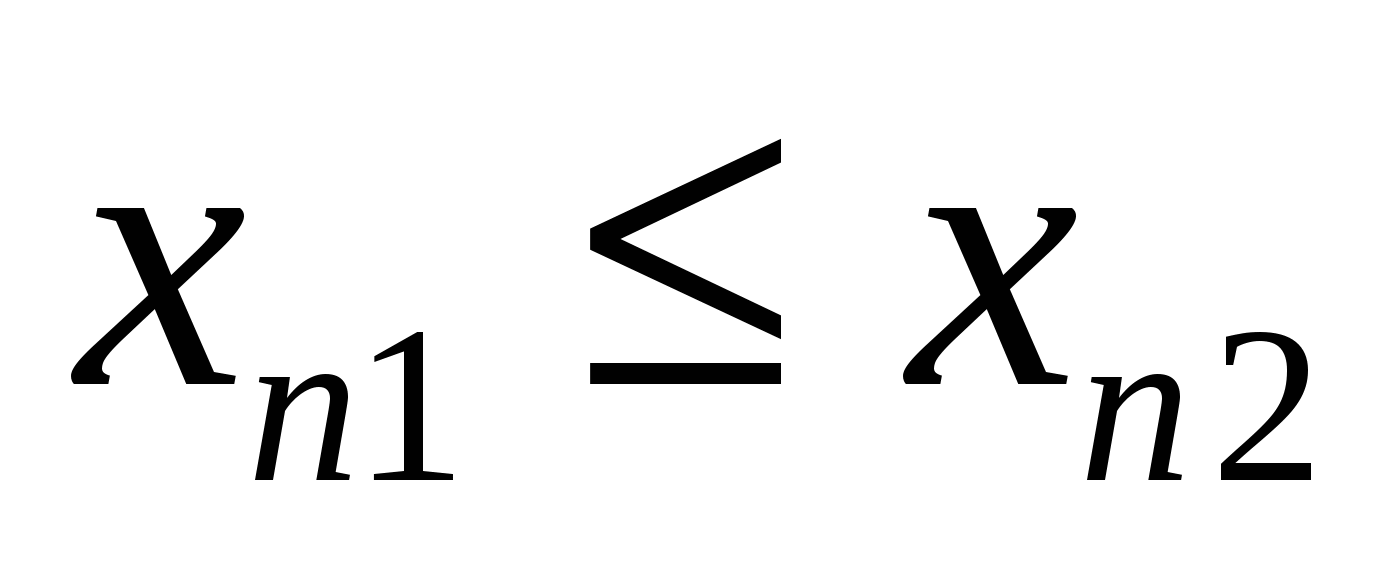 . .
Все перечисленные переменные 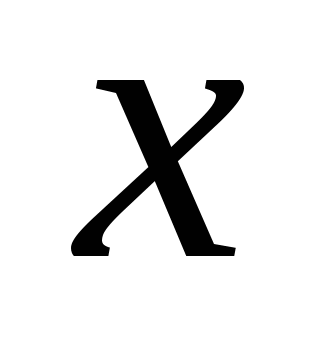 называются монотонными переменными. Они могут быть строго монотонными и не строго монотонными. называются монотонными переменными. Они могут быть строго монотонными и не строго монотонными.
№36. Второй замечательный предел. Следствия. 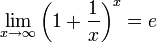 или или 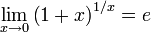
Следствия
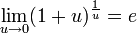
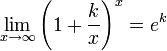
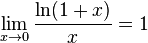
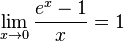
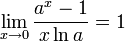 для , для ,
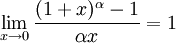
№37.Бесконечно малые и большие.
Опр. 1: Переменная 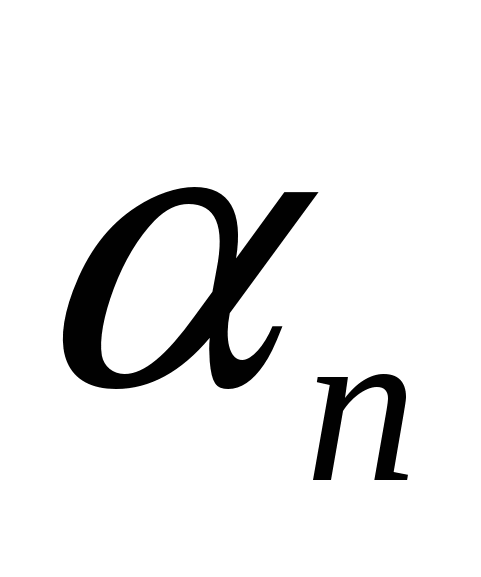 называется бесконечно малой, если её пределом является нуль. называется бесконечно малой, если её пределом является нуль.
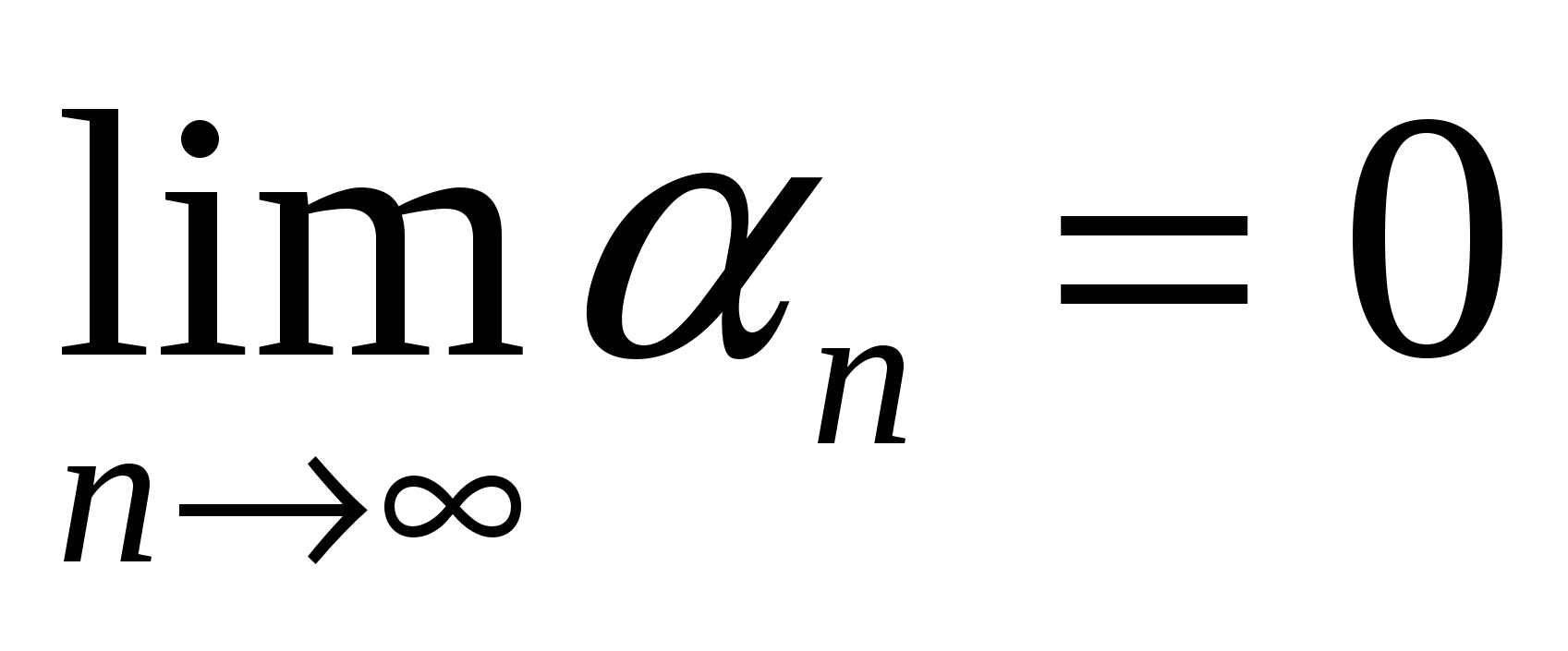
Определение на языке 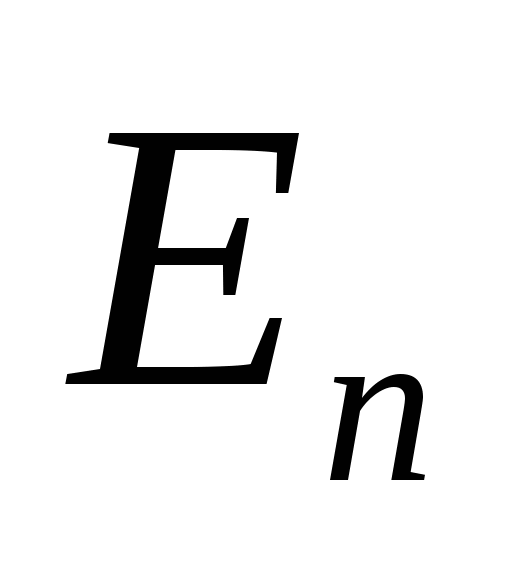 : Переменная : Переменная 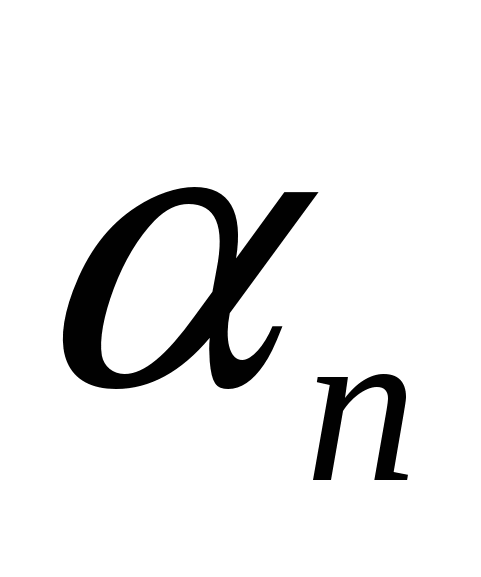 называется бесконечно малой, если для любого E > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства: называется бесконечно малой, если для любого E > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства:
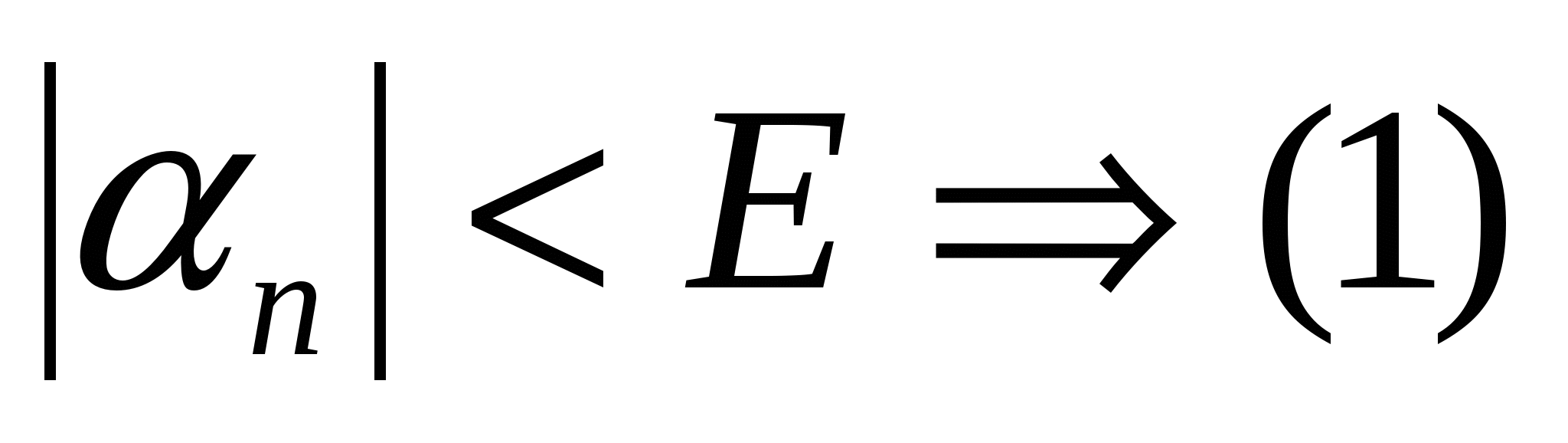
ПРИМЕРЫ:
1. 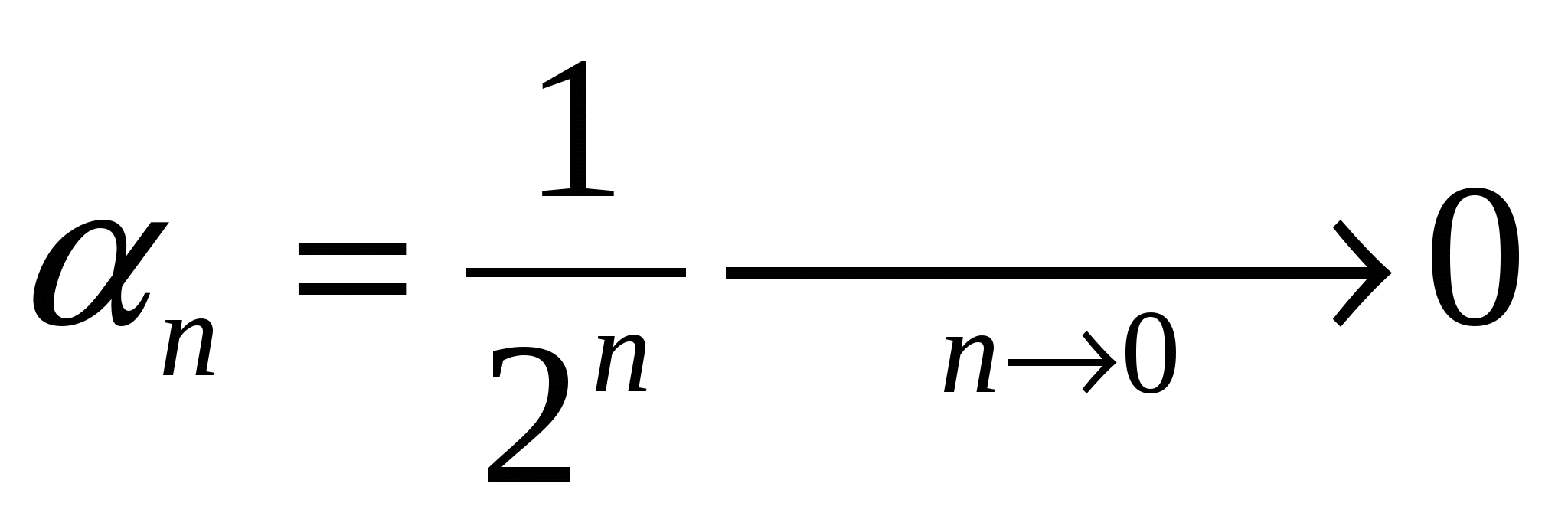
2. 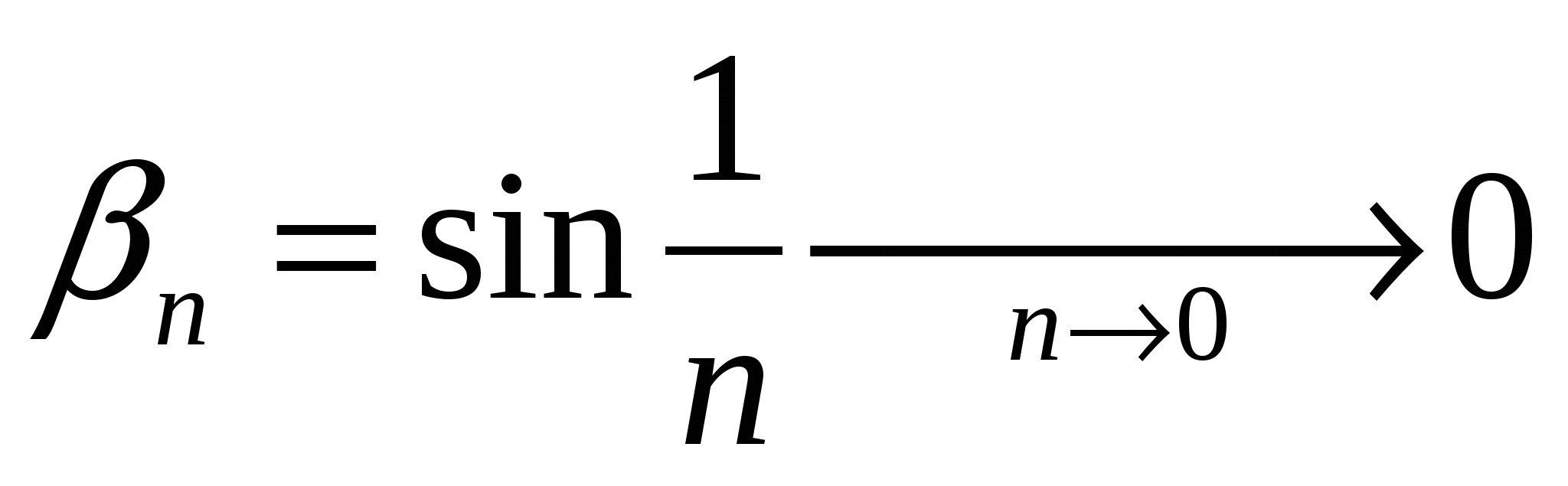
3. 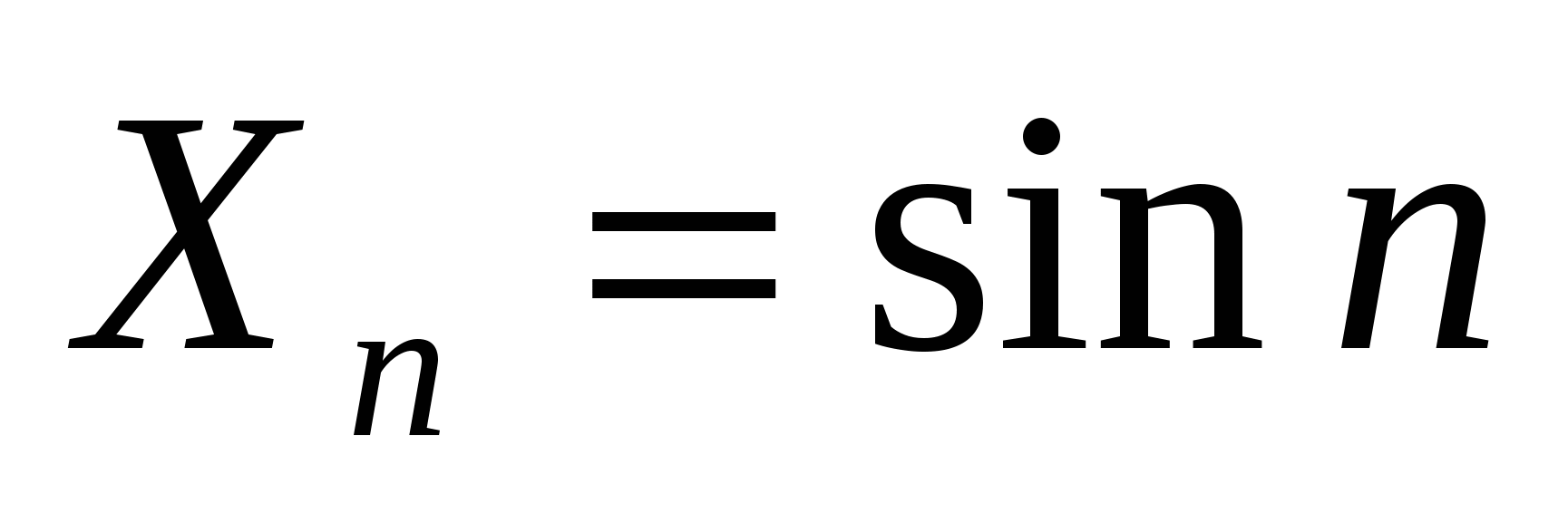 – не имеет предела. – не имеет предела.
БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ.
Опр. 1: Переменная  , называется бесконечно большой, если для любого, сколь угодно большого, числа , называется бесконечно большой, если для любого, сколь угодно большого, числа 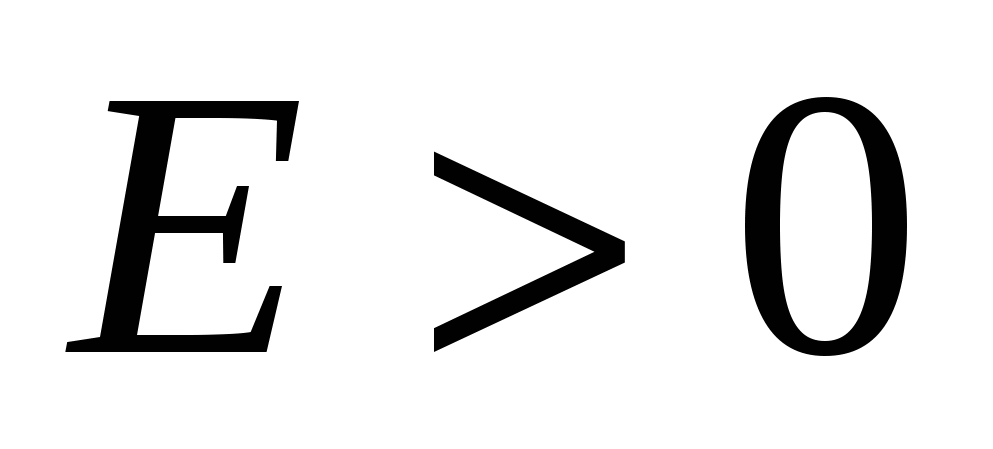 существует такой номер существует такой номер  , что если , что если

Неравенство (1) равносильно объединению 2-х неравенств: 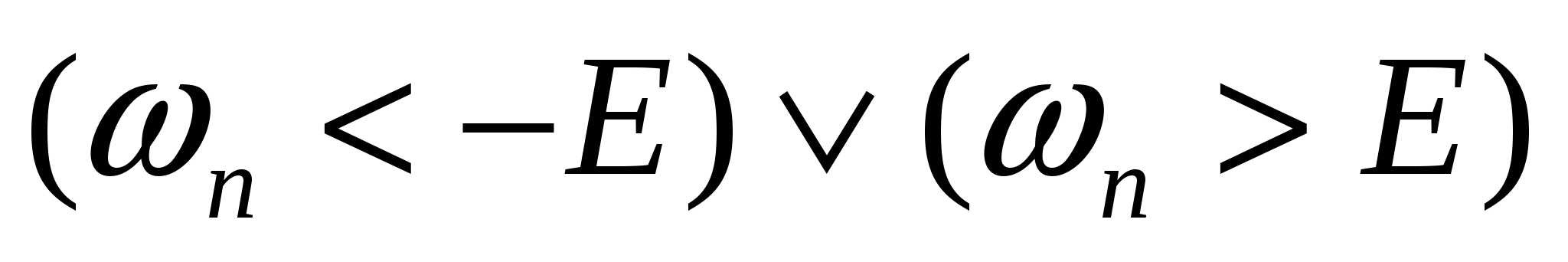 (где (где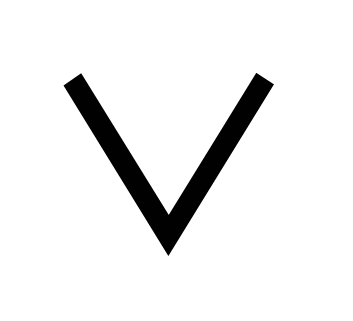 – «или») – «или»)
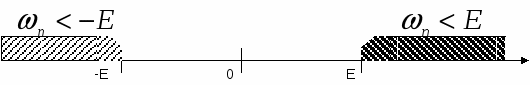
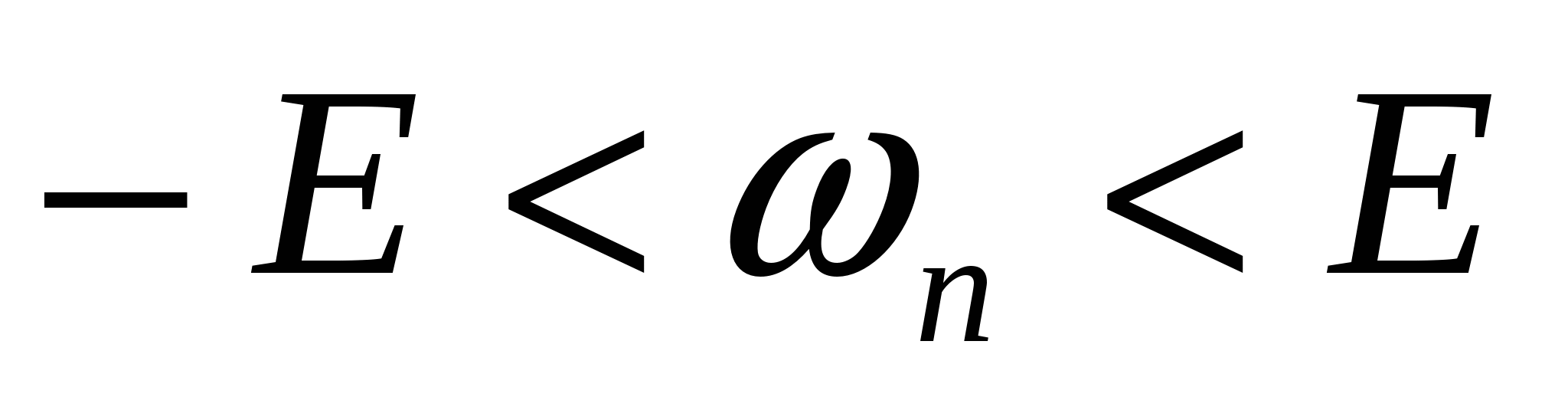
по другому:
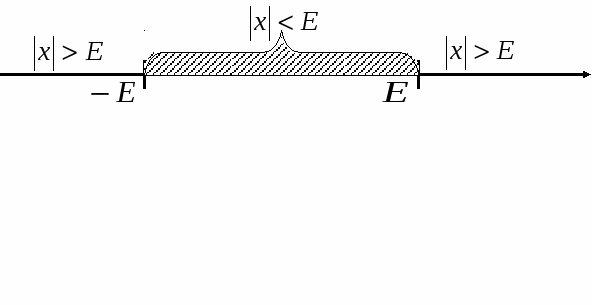
Опр. 2: Объединения 2-х промежутков  , называются , называются  -окрестность бесконечности. -окрестность бесконечности.
Бесконечно большие величины при своём изменении начиная с некоторого номера  попадает в попадает в  окрестность бесконечности и там далее остаётся. окрестность бесконечности и там далее остаётся.
Пример: 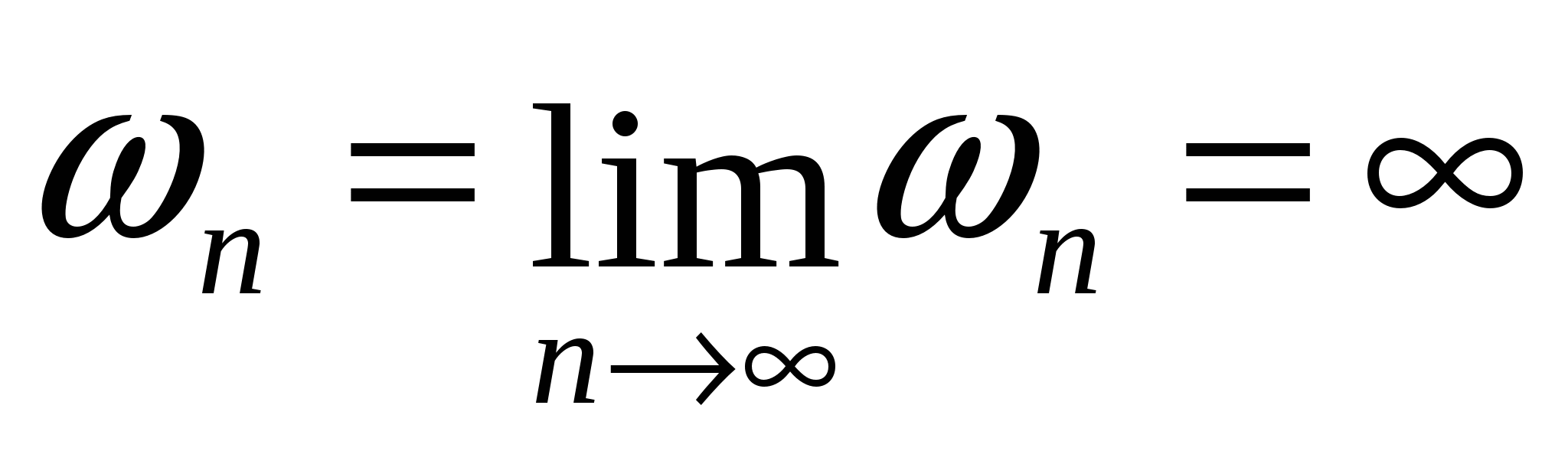 , если , если 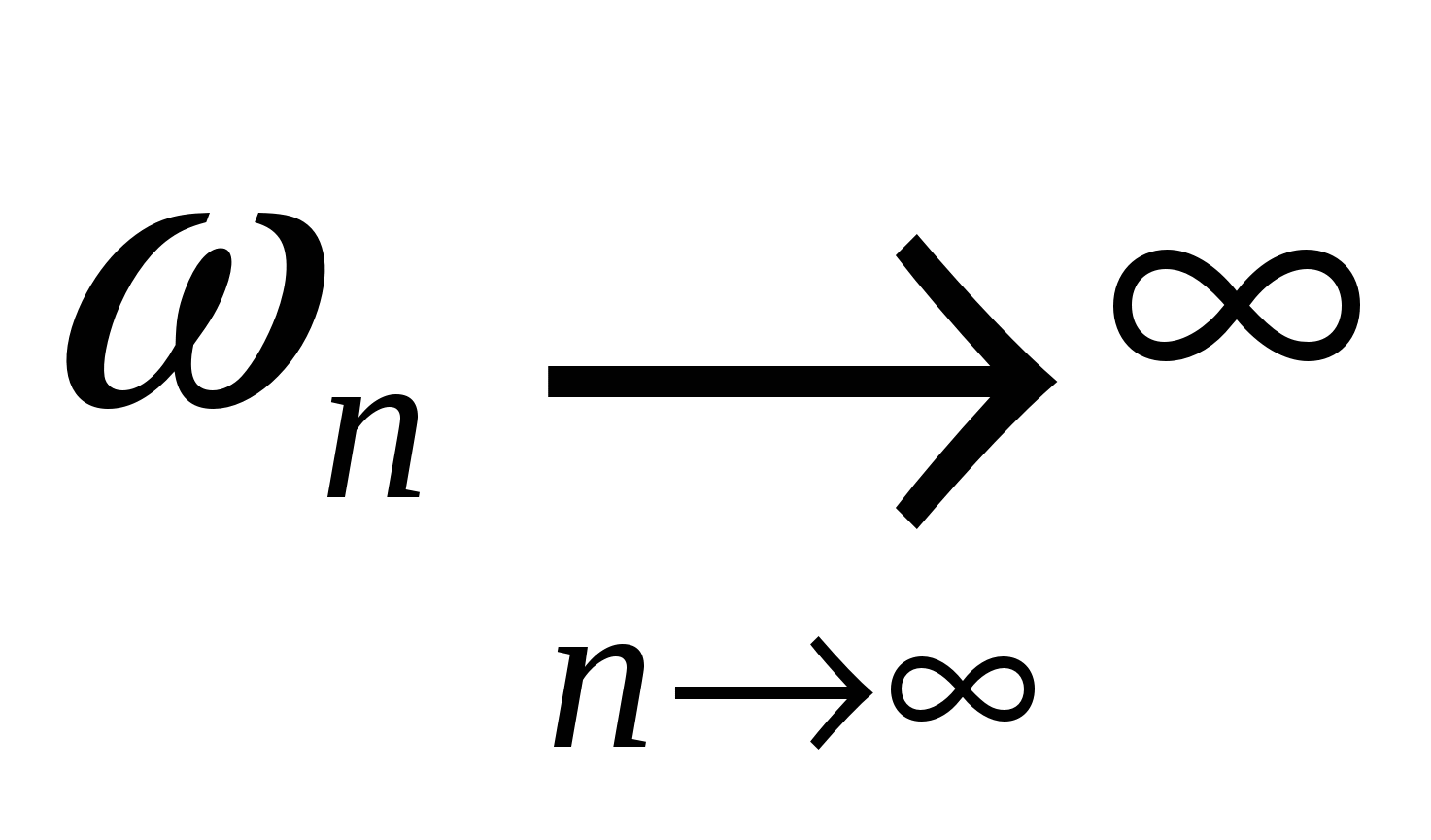
1 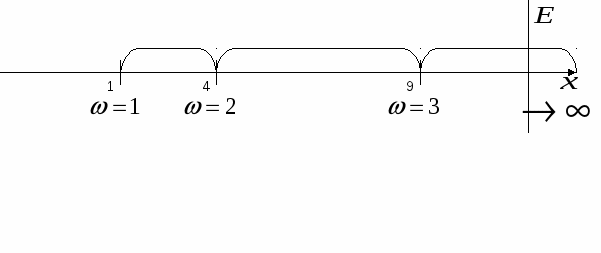 ) ) 
2) 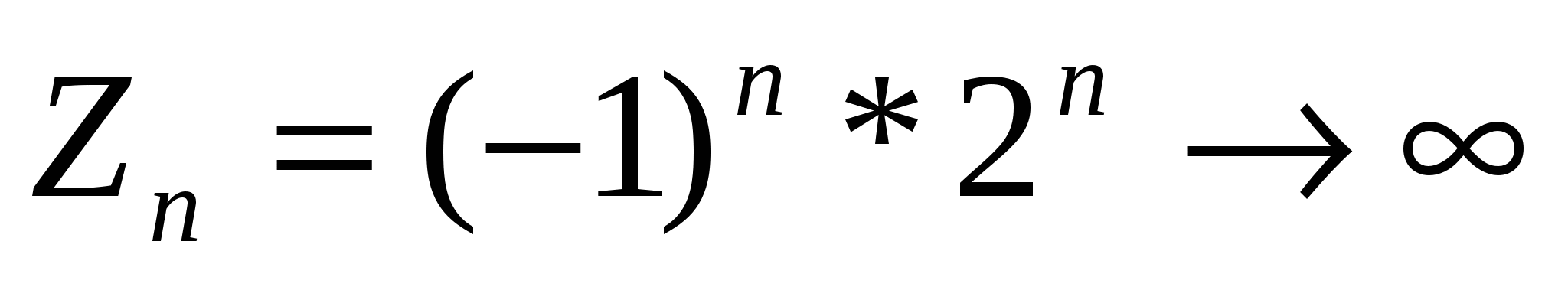
-2, 4, -8, 16, -32, …
n  =1 n=2 n=3 n=4 n=5 =1 n=2 n=3 n=4 n=5
Будем различать положительные и отрицательные бесконечно большие величины
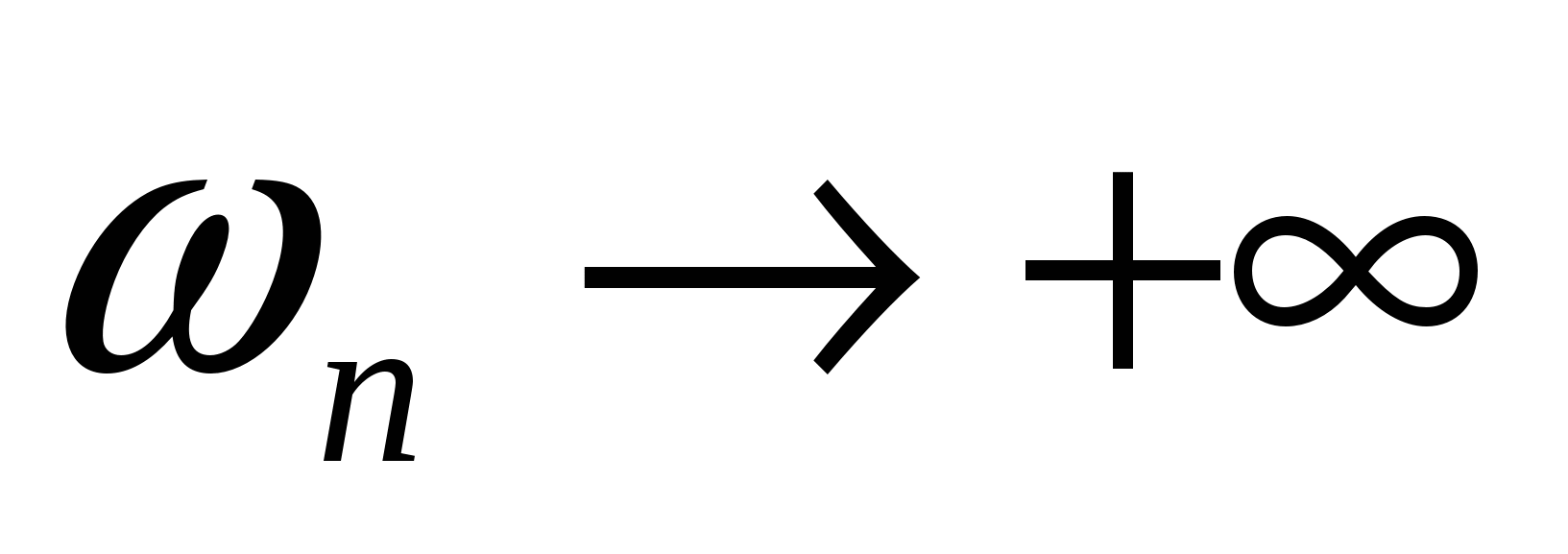 – положительные б.б. – положительные б.б.
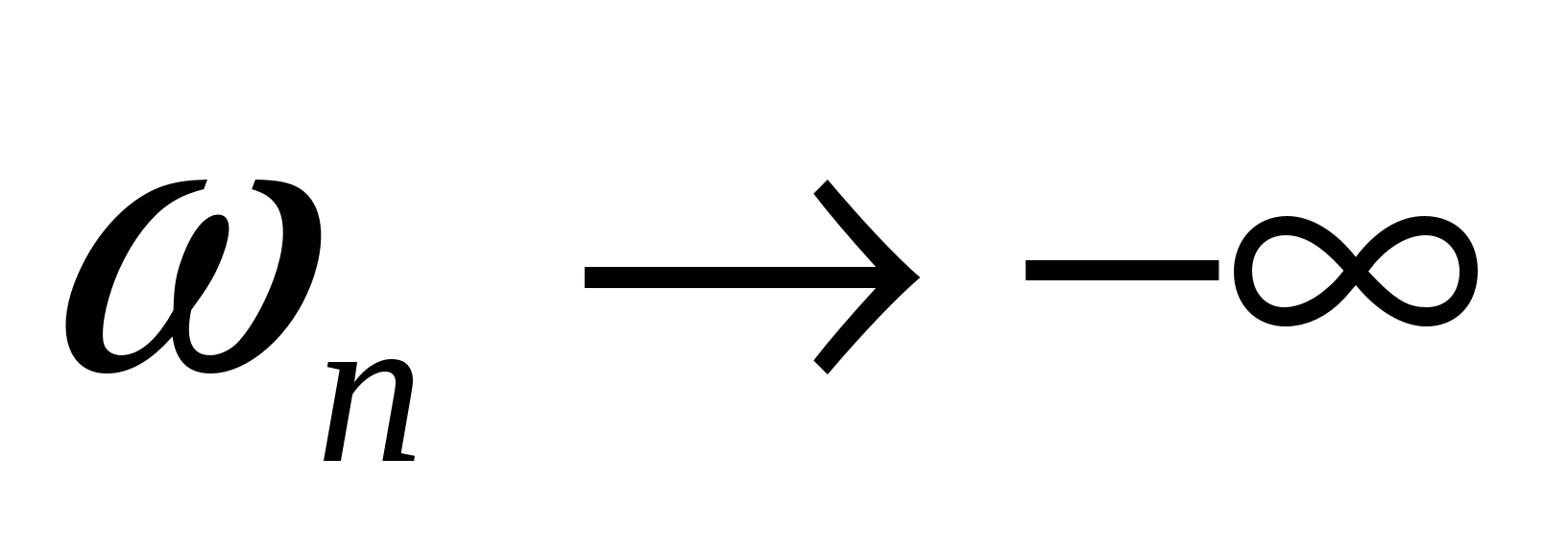 – отрицательные б.б. – отрицательные б.б.
№38. Бесконечно малые функции и их сравнение.
Пусть y=f1(x) и y=f2(x) – некоторые две функции, а x стремится к некоторому x0 (конечному или бесконечному). Если при этом f1(x)→0 и f2(x)→0, то есть если

Это значит, что f2(x) несравненно меньше f1(x) при x→x0 (f2(x) несравненно быстрее, чем , стремится к нулю при x→x0). В этом случае говорят, что функция f2(x) является бесконечно малой функцией более высокого (высшего) порядка малости, чем функция f1(x), при x→x0. И обозначают этот факт так:
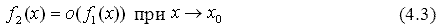
(читается: f2(x) есть «о малое» от f1(x) приx→x0). Суть записи (4.3) состоит, как сказано выше, в том, что бесконечно малая функция f2(x) является бесконечно малой частью другой бесконечно малой функции f1(x) при x→x0.
Вариант 2:
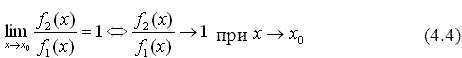
Это значит, что при x→x0 бесконечно малые функции f1(x) и f2(x) практически не отличаются друг от друга. В этом случае говорят, что функция f2(x) эквивалентна (равносильна) функции f1(x) при x→x0. И обозначается это так:

В этом случае говорят, что бесконечно малые при x→x0 функции f1(x) и f2(x) – одного порядка малости. И записывают этот факт так:
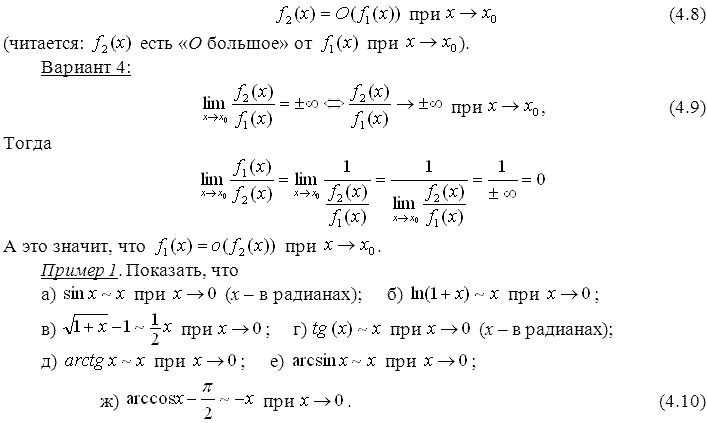
№39. Эквивалентные бесконечно малые.
Если  , то , то 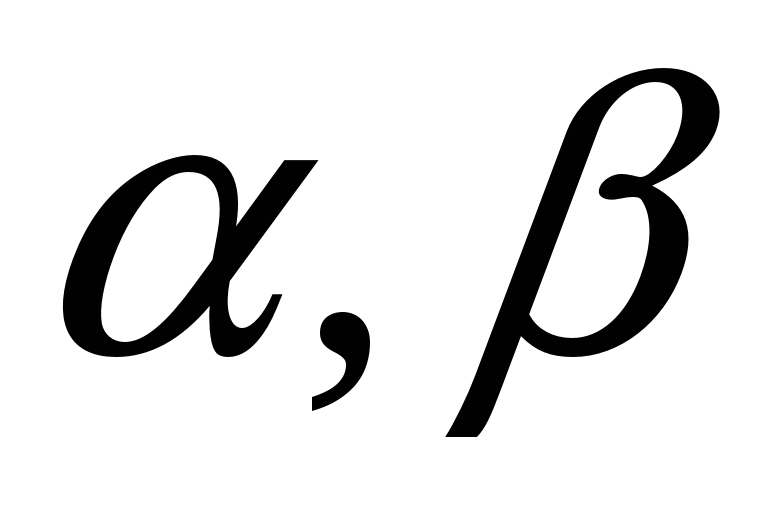 – называются эквивалентными бесконечно малыми величинами. – называются эквивалентными бесконечно малыми величинами.
Запись: 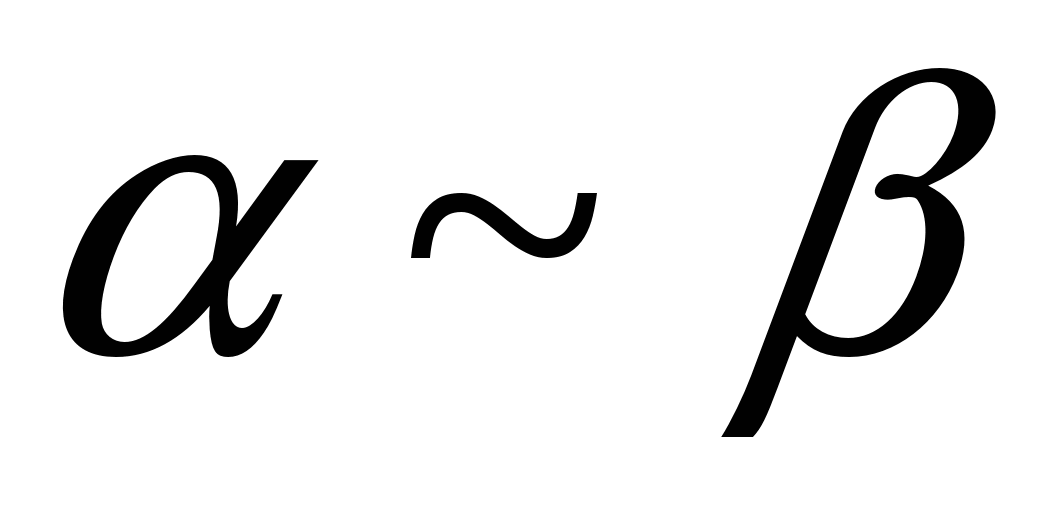
– эквивалентно  . .
№40. НЕПРЕРЫВНОСТЬ ФУНКЦИИ.
Понятие о непрерывности функции описывает непрерывные процессы в округе… Непрерывные функции описывают непрерывные процессы.
Будем обозначать:  – приращение аргумента. – приращение аргумента.
 – приращение функции. – приращение функции.
Опр. 1: Функция  называется непрерывной в точке называется непрерывной в точке  , если она определена в окрестности точки , если она определена в окрестности точки  и бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции и бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции
Под окрестностью точки понимают любую  – окрестность этой точки. – окрестность этой точки.

Запишем 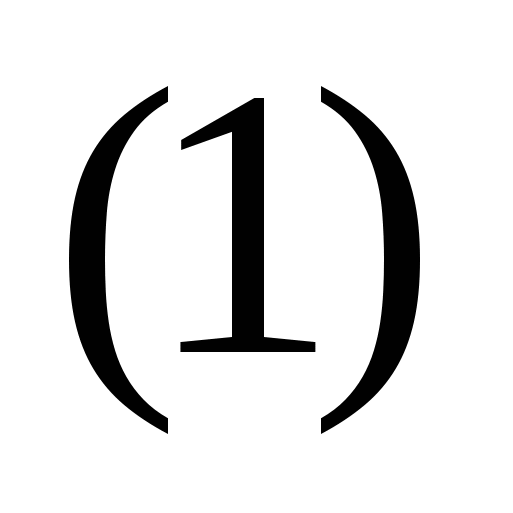 на языке на языке  – окрестностей, используя определение предела функции. – окрестностей, используя определение предела функции.
Опр. 2: Функция  называется непрерывной в точке называется непрерывной в точке 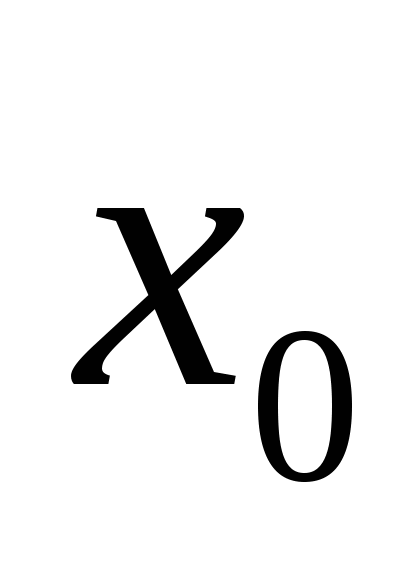 , если она определена в окрестности точки , если она определена в окрестности точки 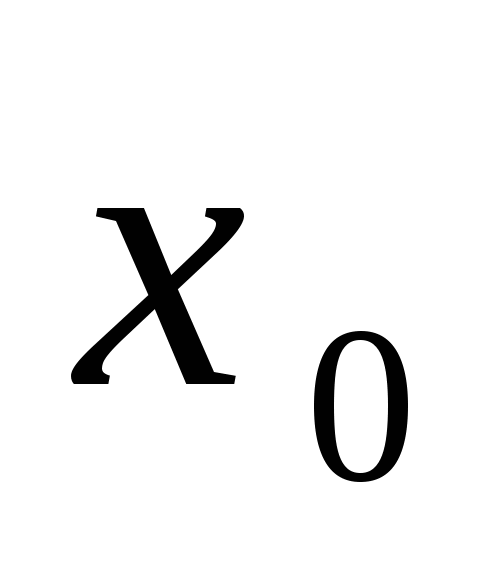 и по любому и по любому 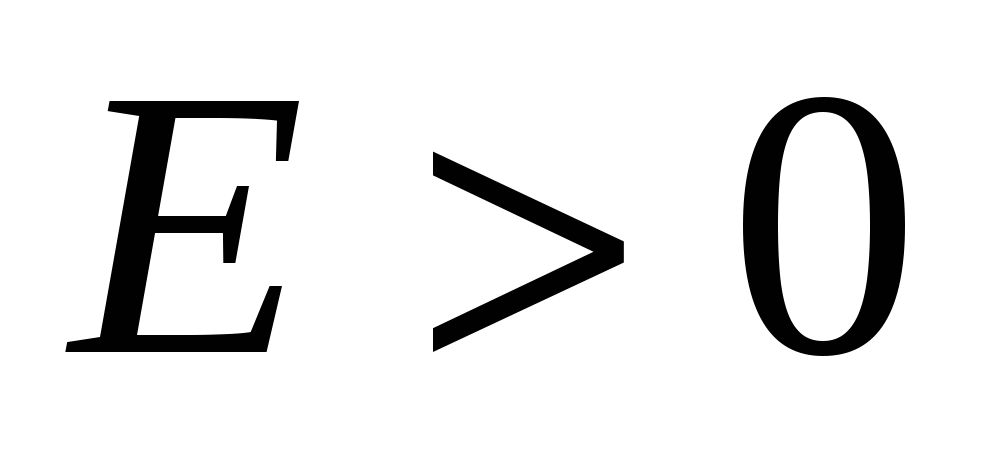 можно указать можно указать 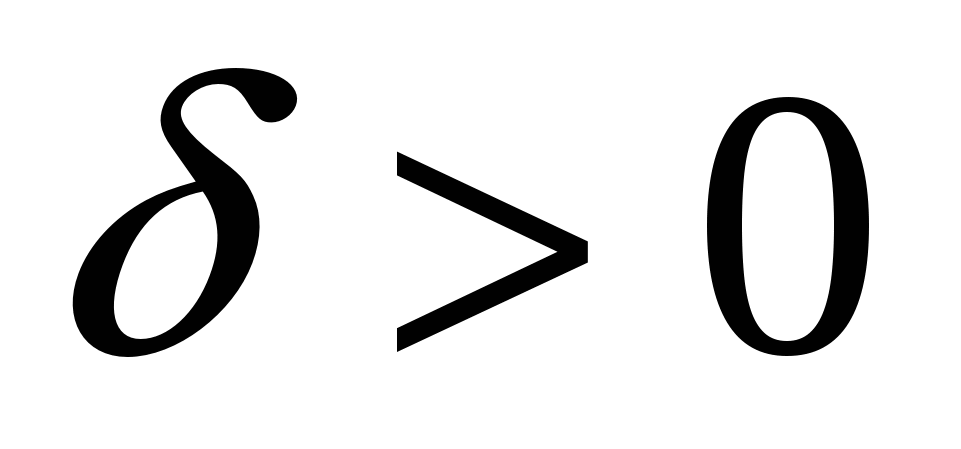 , то при выполнении: , то при выполнении: 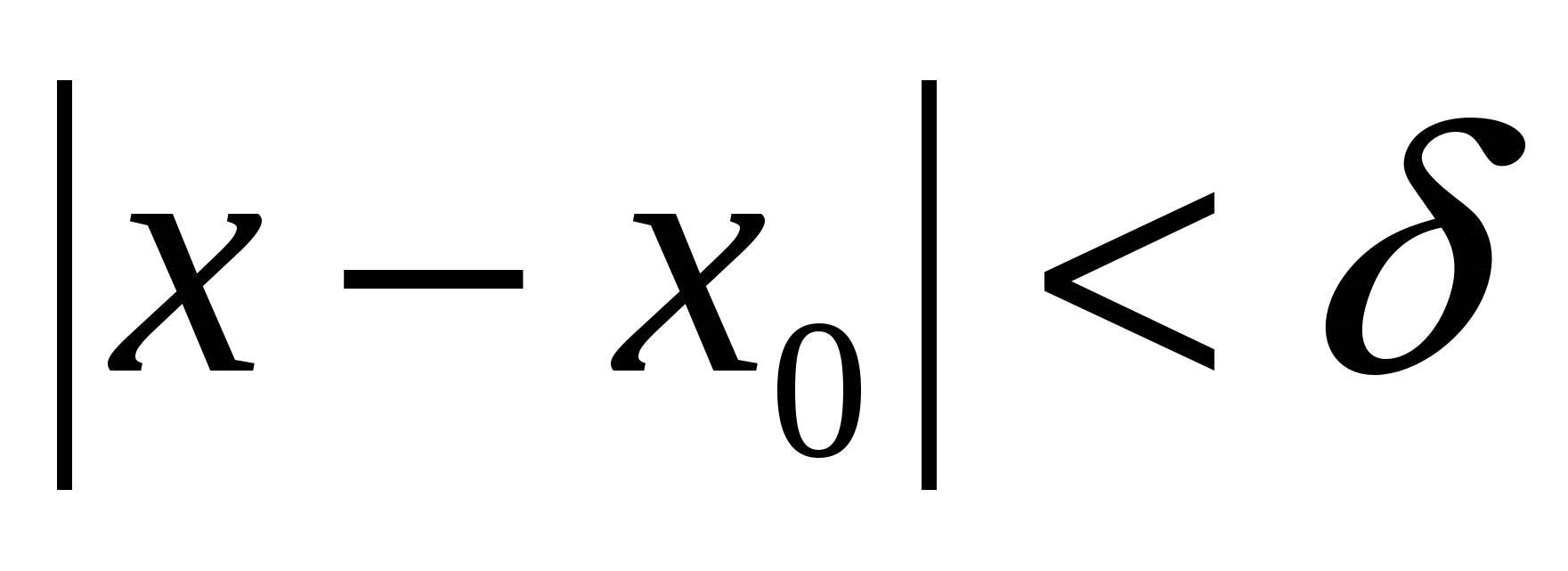 следует: следует: 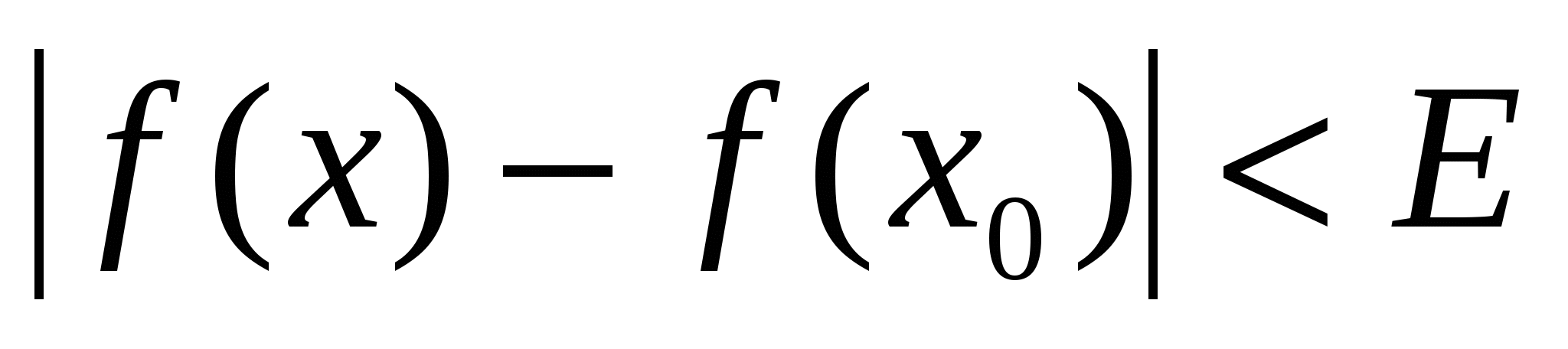
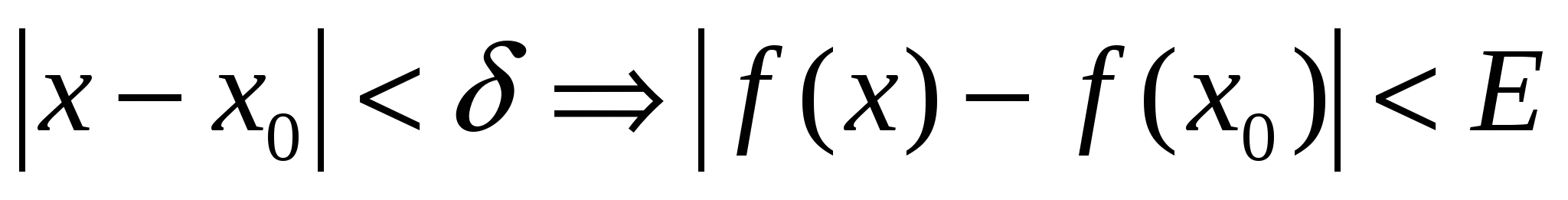
Запишем формулу  ещё в другом виде: ещё в другом виде:
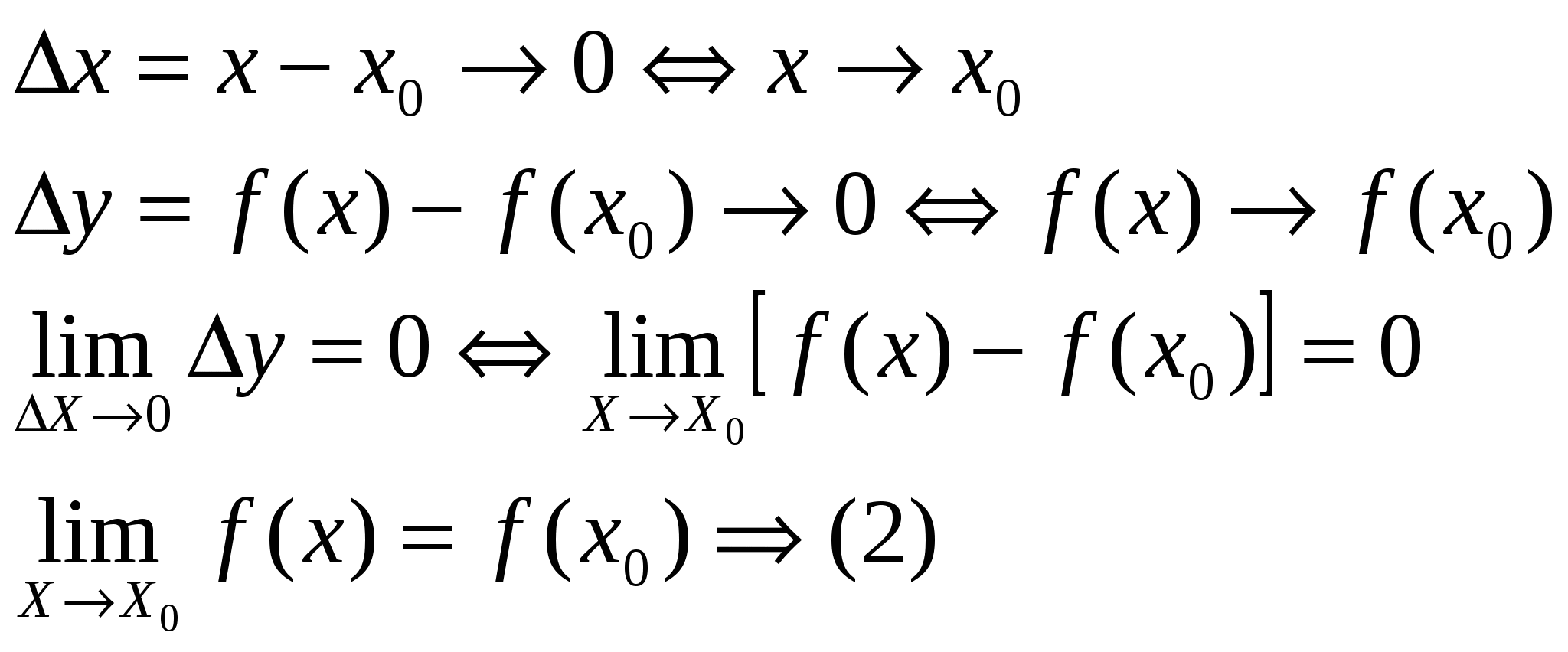
 позволяет сформулировать следующее определение, равносильное предыдущему. позволяет сформулировать следующее определение, равносильное предыдущему.
Опр. 3: Функция  называется непрерывной в точке называется непрерывной в точке 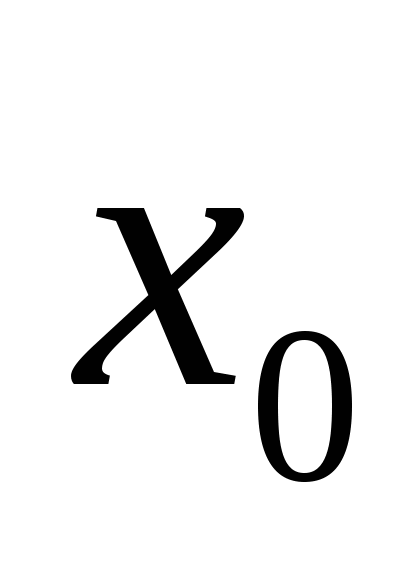 , если она определена в окрестности точки , если она определена в окрестности точки 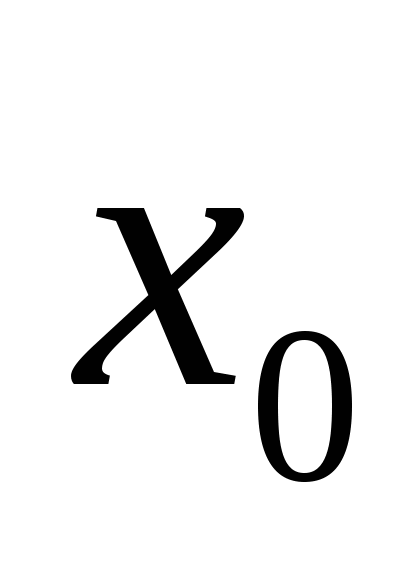 и предел функции равен функции предельного значения аргумента. и предел функции равен функции предельного значения аргумента.
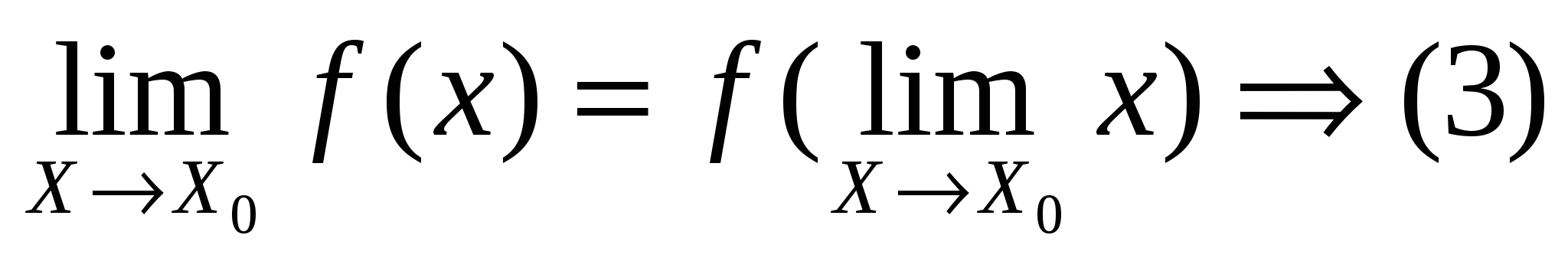
Для непрерывной функции знаки предела и функции можно поменять местами. Запишем уравнение 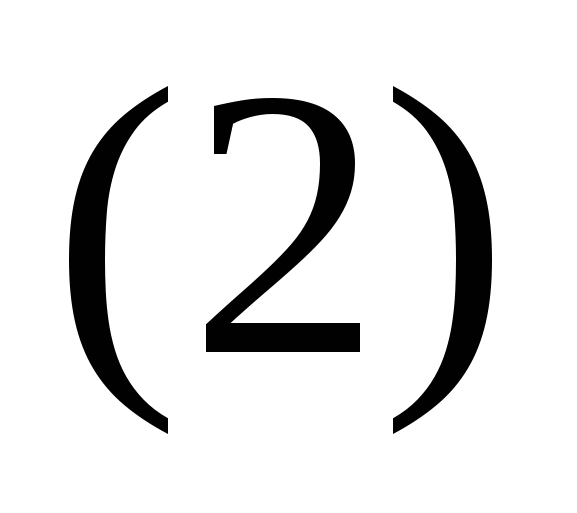 , употребляя пределы с лева и с права. Заметим, что если существует двусторонний предел, то существует оба односторонних предела и они равны между собой, поэтому , употребляя пределы с лева и с права. Заметим, что если существует двусторонний предел, то существует оба односторонних предела и они равны между собой, поэтому 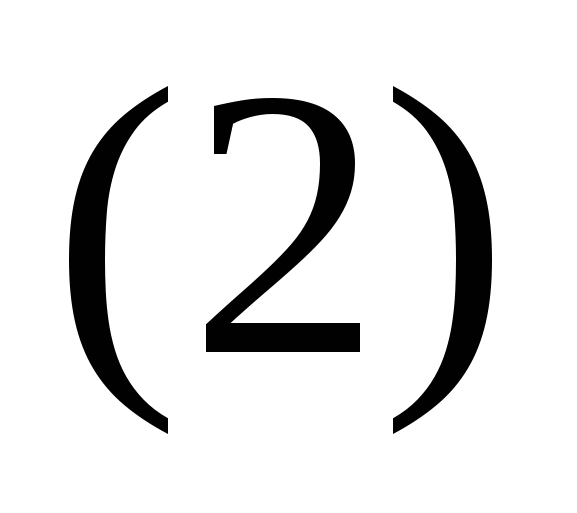 может быть записана в следующей эквивалентной форме: может быть записана в следующей эквивалентной форме:
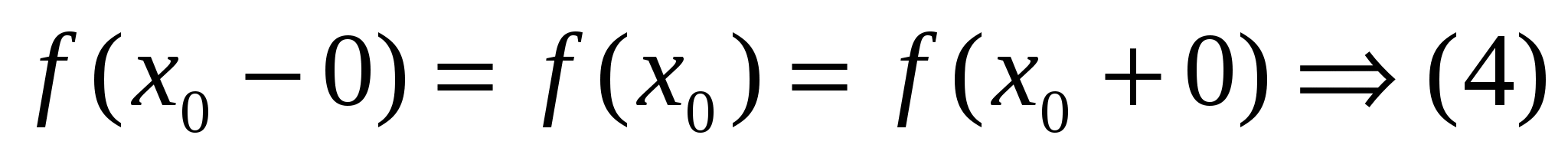
Опр. 4:Функция  называется непрерывной в точке называется непрерывной в точке 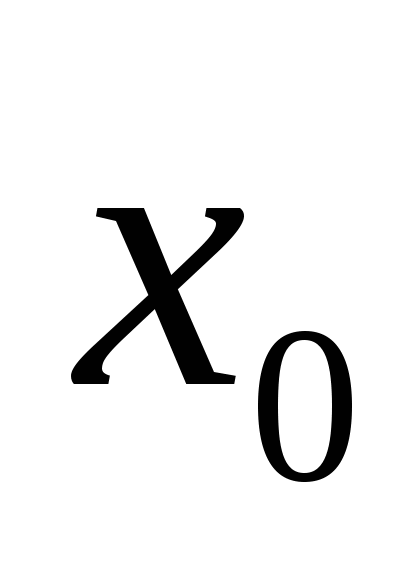 , если она определена в окрестности точки , если она определена в окрестности точки  , существуют конечные пределы с лева и с права и выполняется равенство: , существуют конечные пределы с лева и с права и выполняется равенство: 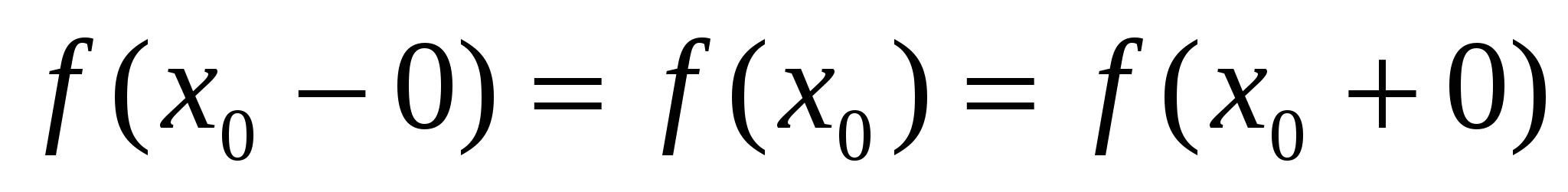 . .
Пределы с лева и справа равны между собой и равны значению функции в точке.
Опр. 5: Функция  называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка. называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка.
№41. Необходимые и достаточные условия непрерывности
Точка  называется точкой разрыва функции называется точкой разрыва функции  , если нарушается хотя бы одно из условий определения непрерывности функции; используем опр. 4: , если нарушается хотя бы одно из условий определения непрерывности функции; используем опр. 4:
Нарушение: – Условие:
1. 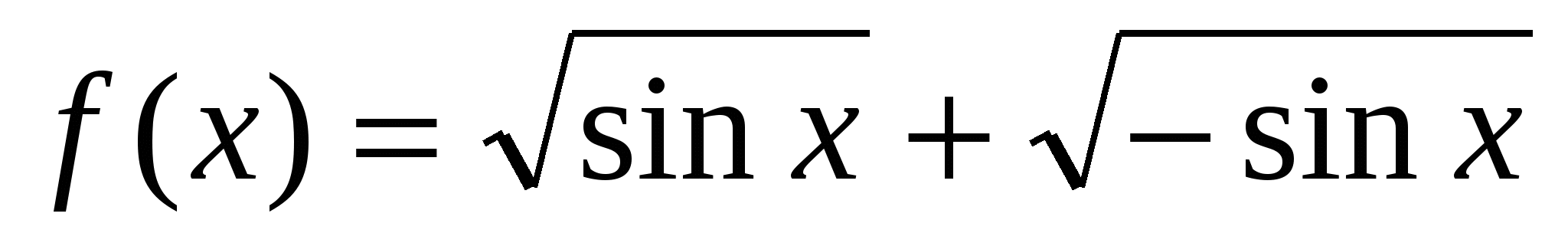
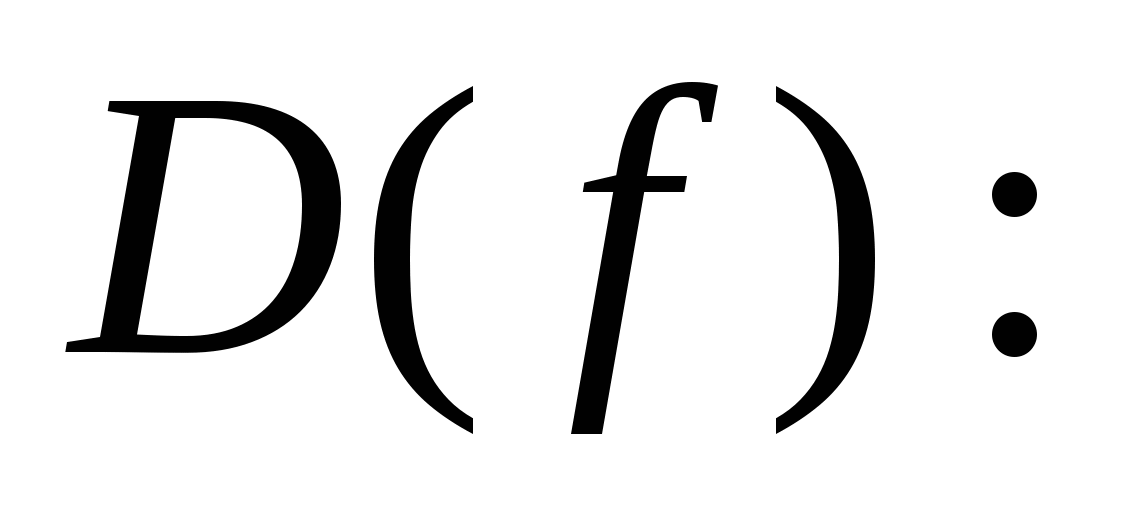 Функция определена в точках, где Функция определена в точках, где 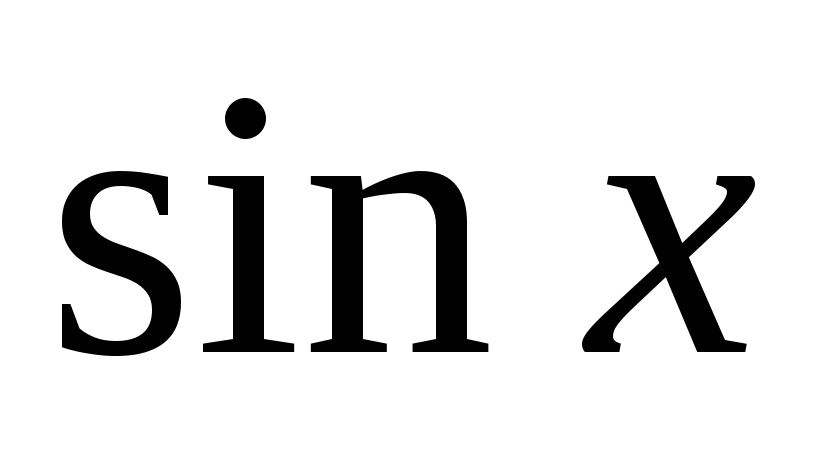 обращается в ноль. обращается в ноль.
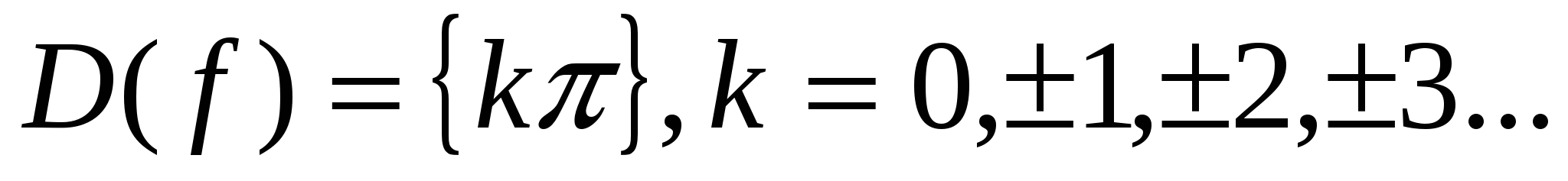
Эта функция разрывна во всех точках области определения функции, т. к. эти точки изолированы без окрестности.
2. Если пределы с лева и с права не являются конечными |
|
|
 Скачать 1.62 Mb.
Скачать 1.62 Mb.