матан шпора. Упорядоченность

• Название: Упорядоченность
• Анкор: матан шпора.doc
• Дата: 18.01.2018
• Размер: 1.62 Mb.
• Имя файла: матан шпора.doc
• Тип: Документы; #14460
• страница: 4 из 6

Доказательство

Поделим с остатком многочлен  на многочлен :



Так как , то  — многочлен степени не выше 0. Подставляя , поскольку , имеем .

[править]Следствия

• 
  Число a является корнем многочлена  тогда и только тогда, когда  делится без остатка на двучлен  (отсюда, в частности, следует, что множество корней многочлена  тождественно множеству корней соответствующего уравнения ).
  
• 
  Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
  
• 
  Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.
  

№21.Числовая ПОСЛЕДОВАТЕЛЬНОСТЬ

Опр. 1: Последовательностью называется множество чисел, пронумерованных с помощью чисел и расположенных в порядке возрастания номеров.



– общий член последовательности.



N – номер члена последовательности, играет роль аргумента функции. Фактически задает последовательность целочисленных аргументов.

– функция целочисленных аргументов.

Выражение примеров последовательности:

ПРИМЕРЫ:

1. – о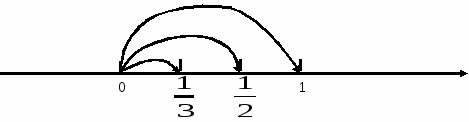бщий член последовательности.

;

2.

Будем различать последовательности, имеющие предел, и не имеющие предела. Общий член последовательности – переменная величина, значение которого определяется номером N. Эта величина является функцией аргумента N



№22. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ.

Опр. 1: Постоянное число называется пределом переменной, если для любого сколь угодно малого числа , существует такой номер , что при выполнении неравенства следует выполнение неравенства:



В силу леммы о вещественных числах (№1) одно неравенство с модулем (1) равносильно двойному неравенству:



Неравенство (2) определяет на оси E так называемую E – окрестность точки a.

Неравенство (2) означает, что переменная точка находится в E – окрестности точки a.

Постоянное число a называется пределом переменной 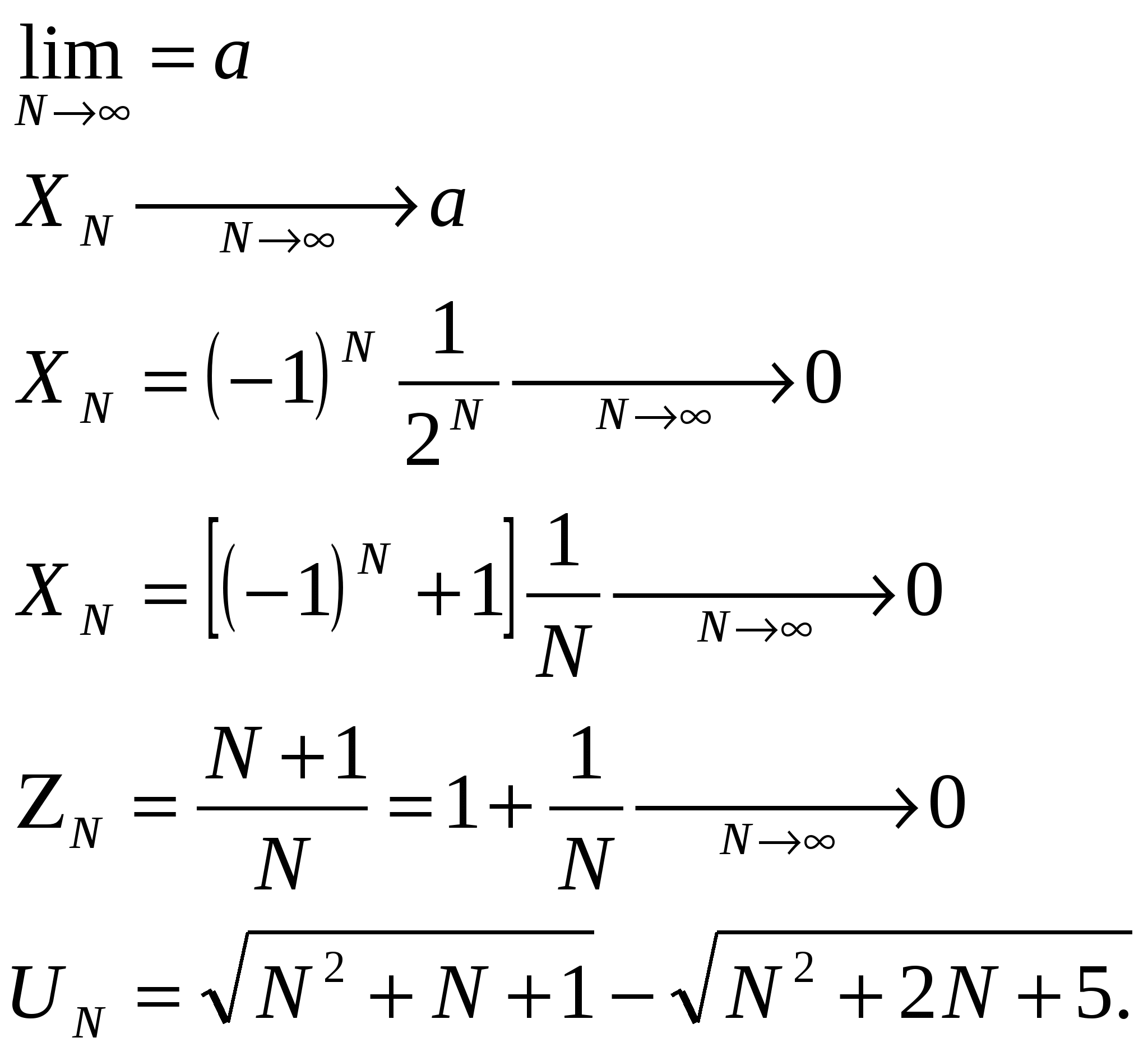, если для любой сколь угодно малой E – окрестности точки a начиная с некоторого номера n (n > N), точка попадает в эту E – окрестность, и при своем дальнейшем изменении будет там находиться.



№23. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ. И большие

Опр. 1: Переменная называется бесконечно малой, если её пределом является нуль.



Определение на языке : Переменная называется бесконечно малой, если для любого E > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства:



ПРИМЕРЫ:

1.

2.

3. – не имеет предела.

ЛЕММЫ О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ.

ЛЕММА №1:

Для того чтобы переменная 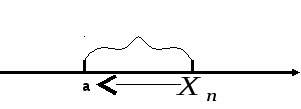имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:



– бесконечно малая величина.



Результат следует из того, что разность 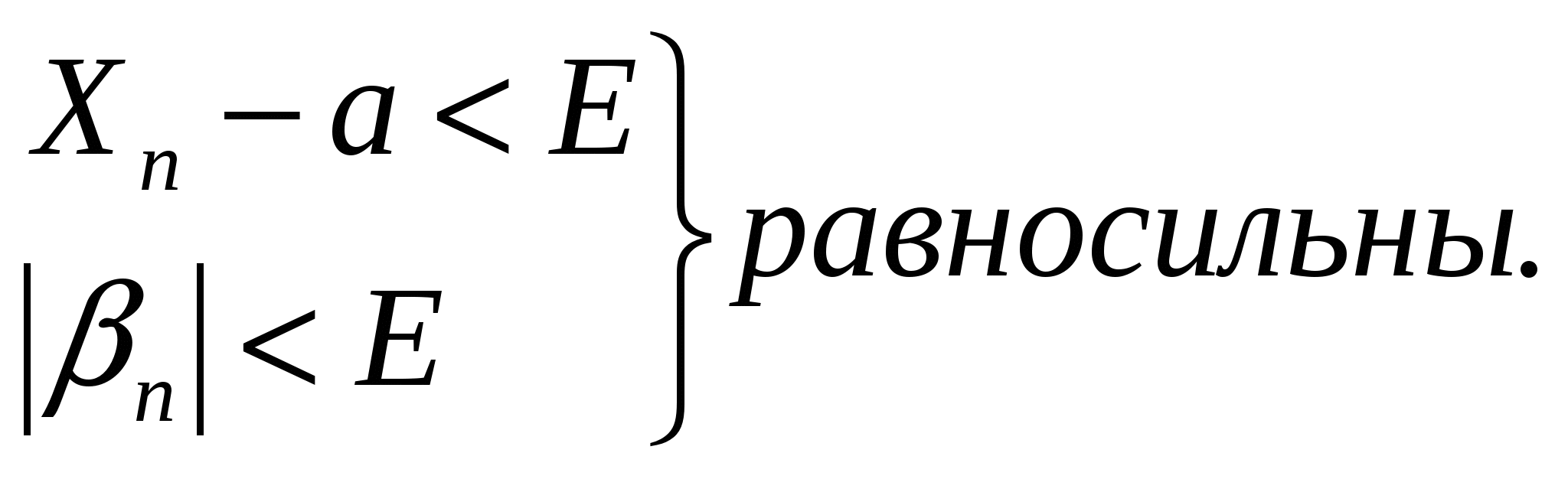есть расстояние от точки до её предела , это расстояние стремится к нулю, т. к. , и наоборот: если расстояние стремиться к нулю, то .



ЛЕММА №2:

Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Опр. 2: Переменная 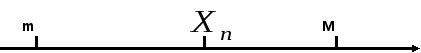называется ограниченной, если существуют такие m и M , что для всех выполняется равенство:



ПРИМЕР:

1. 
   Sin n – ограниченное, т. к. |sin n| ≤ 1.
   
2. 
   
   

3. – не является ограниченным.

(О. П. – ограниченная переменная).

ЛЕММА №3:

Произведение о. п. на б. м. есть величина б. м.

Пусть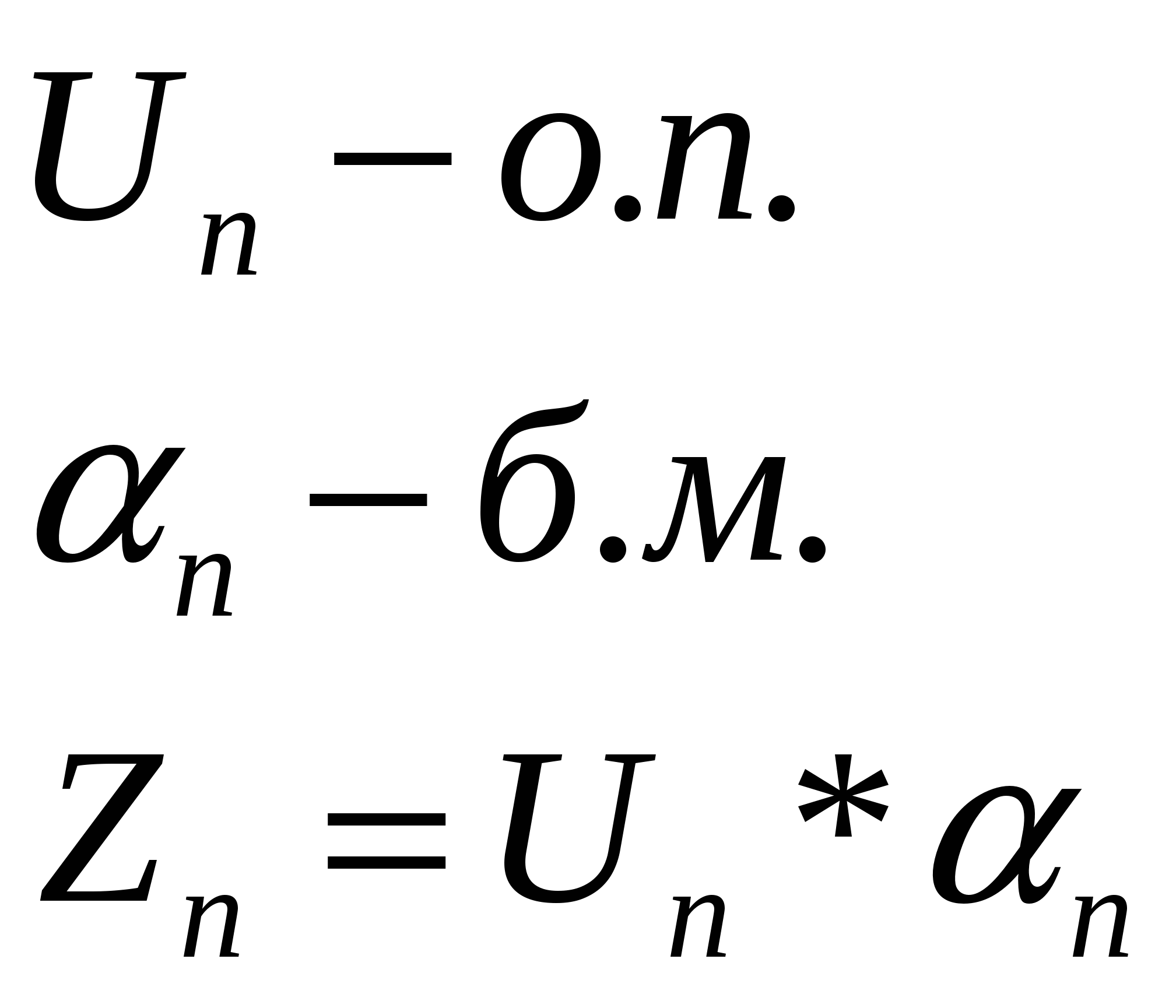

БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ.

Опр. 1: Переменная , называется бесконечно большой, если для любого, сколь угодно большого, числа существует такой номер , что если



Неравенство (1) равносильно объединению 2-х неравенств: 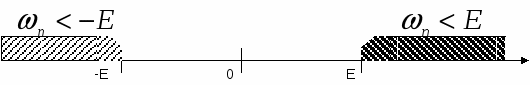(где – «или»)





по другому: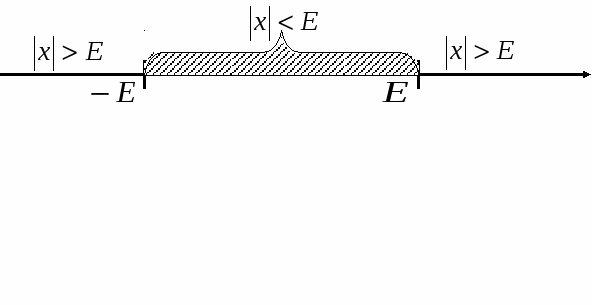



Опр. 2: Объединения 2-х промежутков , называются -окрестность бесконечности.

Бесконечно большие величины при своём изменении начиная с некоторого номера попадае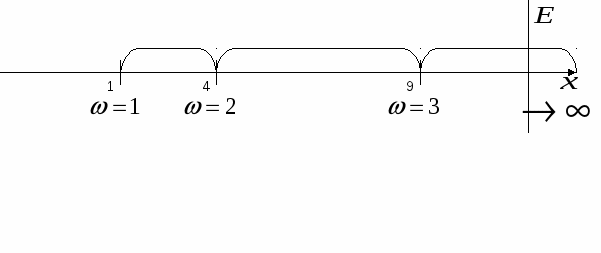т в окрестность бесконечности и там далее остаётся.

Пример: , если

1)

2)

-2, 4, -8, 16, -32, …

n=1 n=2 n=3 n=4 n=5

Будем различать положительные и отрицательные бесконечно большие величины

– положительные б.б.

– отрицательные б.б.

ЛЕММЫ О БЕСКОНЕЧНО БОЛЬШИХ.

ЛЕММА №1:

Величина обратная бесконечно малой есть бесконечно большая величина, и обратно…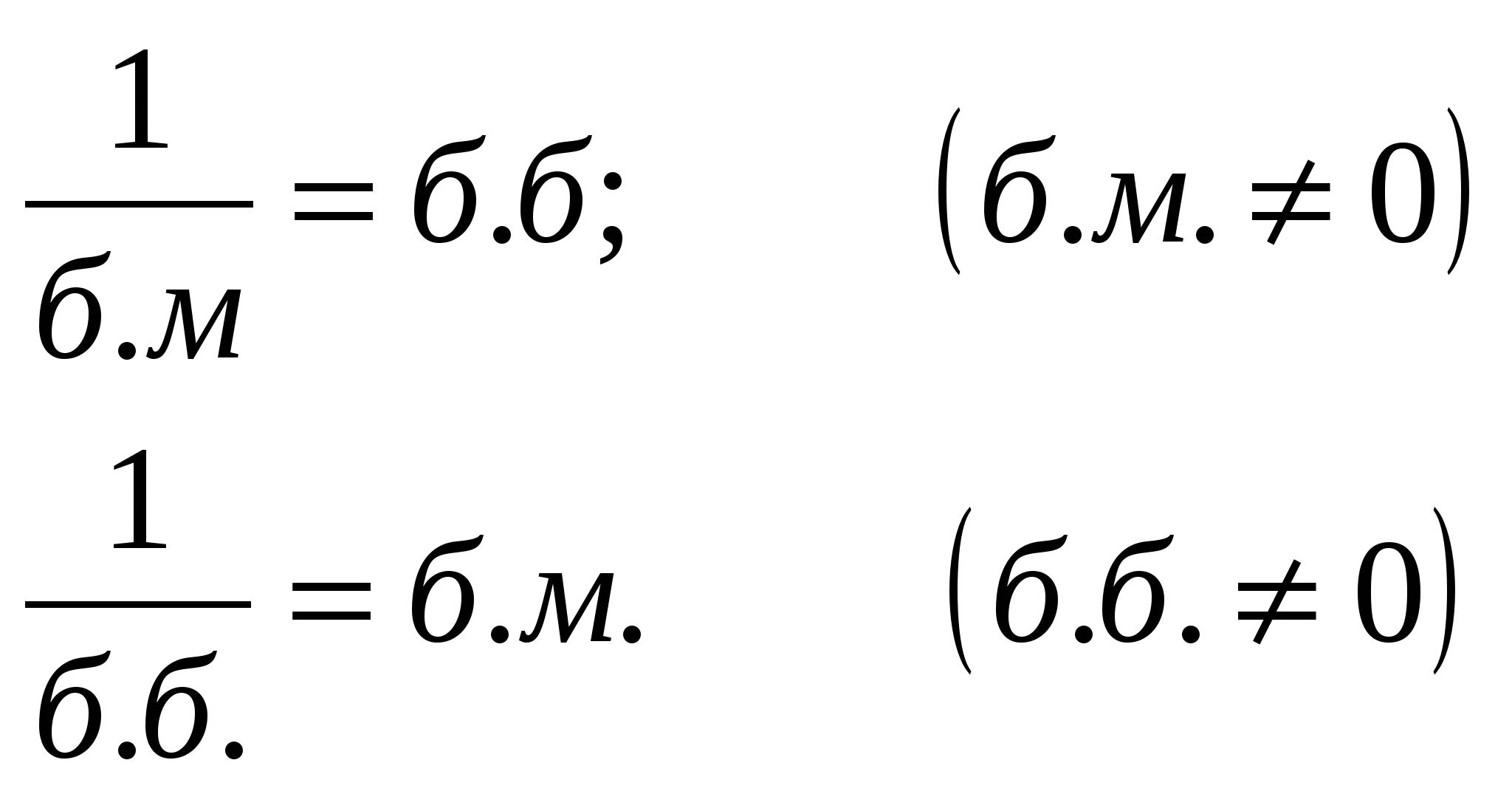



ЛЕММА №2:

Произведение бесконечно большой величины на переменную, стремящуюся к конечному пределу отличного от нуля, есть бесконечно большая величина.





№24.  Бесконечный предел.

Условная запись



обозначает, что для любого E > 0 справедливо неравенство:

|f(x)| > E, если только 0 < |x - a| < δ (E) .

два замечательных предела:

1) 

2)

№25.Свойства сходящихся последовательностей.

Теорема 1. Сходящаяся последовательность имеет только один предел
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Теорема 3. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}.

Теорема 4. Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn}


Теорема 5. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}.
Лемма 1. Если последовательность {yn} сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное {1yn}  последовательностей {\{}1{\}} и {yn}, которое представляет собой ограниченную последовательность.
Теорема 6. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.