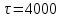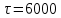курсовая. Управление системами и процессами технической эксплуатации летательных аппаратов
 Скачать 408.52 Kb.
|
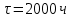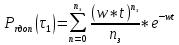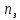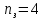1.2. Определение возможной длительности эксплуатации изделий для парка ЛА с учетом замены отказавших и при наличии заданного количества запчастей на складе авиапредприятия.Начнем расчет с  и на каждом шаге будем добавлять 2000ч считаем по формуле: где,  - кол-во запасных частей Выполним расчет для 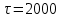 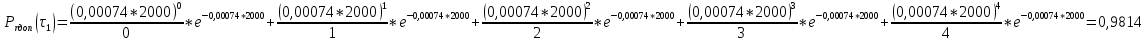 Остальные расчеты сведем в табл.1.4 Табл.1.4 Расчет ресурса
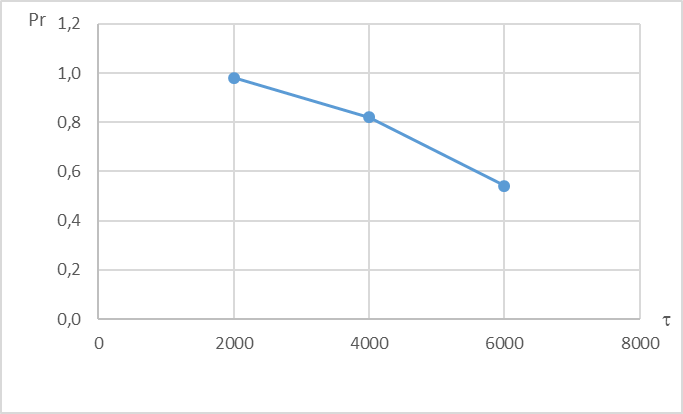 Исходя из расчетов строим график (рис 1.3) Рис.1.3 Функция распределения наработки до отказа при заданном кол-ве деталей Таким образом при заданном количестве запчастей на складе, оптимальный назначенный ресурс составит ≈6000 ч. Вывод по задаче №1: Исходя из проделанной работы оптимальное число запасных клапанов на складе, при заданных параметрах эксплуатации составляет 160. Большее количество запчастей приведет к неэкономному расходованию средств, меньшее приведет к росту простоев, связанных с отсутствием необходимого числа изделий. При заданном количестве запчастей на складе, оптимальный назначенный ресурс составит ≈6000 ч. Больший ресурс приведет к большему числу отказов изделий и превысит , меньший ресурс экономически нецелесообразен. 2.1 Определение зависимости параметра изделия от наработки для математического ожидания и среднего квадратического отклонения по статистическим данным эксплуатационных наблюдений при двух фиксированных значениях наработки | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант | 6 | ||||
| Исследуемый параметр | Объемный КПД γ | ||||
 |  | ||||
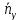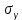| Наработка t, ч | 0 | 0,929 | 0,011 | ||
| 500 | 0,904 | 0,026 | |||
| 1000 | 0,893 | 0,048 | |||
| Доверительная вероятность α | 0,9 | ||||
В качестве двух точек выберем t1=500 ч. и t2=1000 ч.
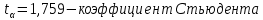
1. Определим коэффициент долговечности А:
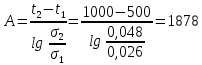
2. Вычислим коэффициент смещения:
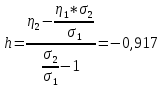
3. Вид функциональной зависимости для мат. ожидания η:
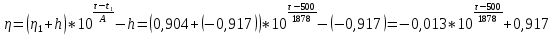
4. Вид функциональной зависимости для верхней доверительной границы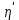 
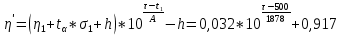
5. Вид функциональной зависимости для верхней доверительной границы
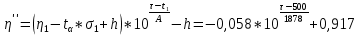
6. Вид функциональной зависимости для скорости изменения параметра V
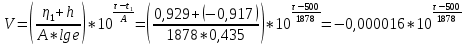
7. Построим зависимости величин при наработках t1, t2, t3
С учетом полученных зависимостей спрогнозируем математическое ожидание, верхний и нижний доверительные пределы, и скорость изменения параметра для времени
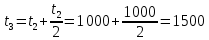
Расчет сведем в табл.2.2
Табл.2.2
| t | 500 | 1000 | 1500 |
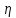 | 0,90 | 0,89 | 0,87 |
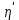| | 0,95 | 0,98 | 1,03 |
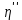 | 0,86 | 0,81 | 0,72 |
| V | 0,000016 | 0,000029 | 0,000054 |
Графическое изображение указанных зависимостей представлено на рис. 2.1 и рис.2.2.
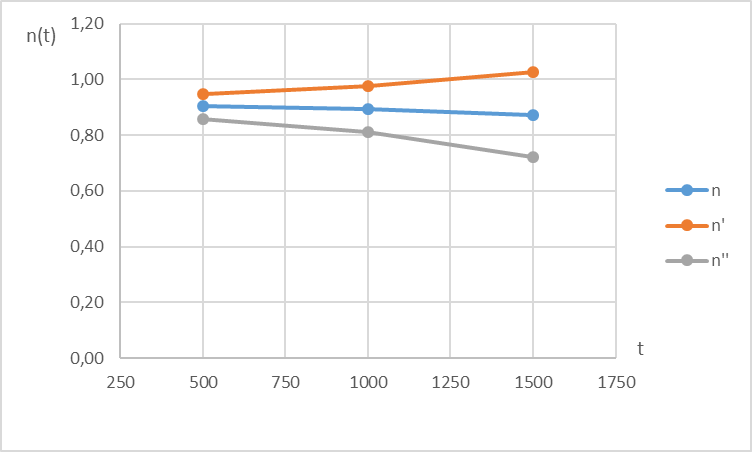
Рис.2.1 Прогноз зависимости значения параметра от наработки
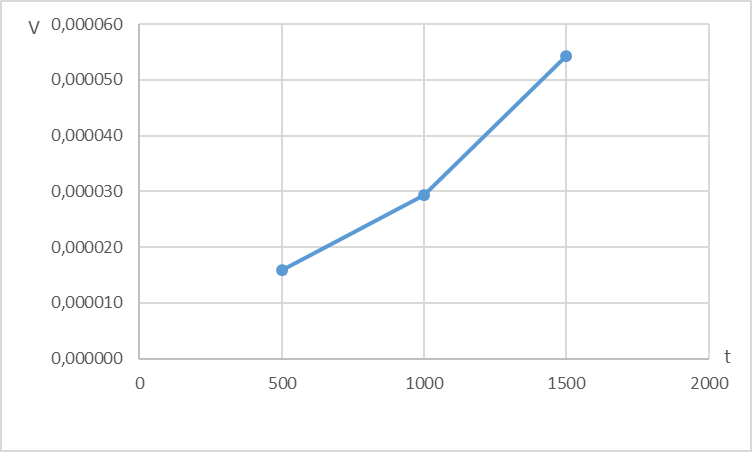
Рис.2.3 Прогнозируемая зависимость значения скорости изменения параметра от наработки
2.2 Определение зависимости параметра изделия от наработки для математического ожидания и среднего квадратического отклонения по статистическим данным эксплуатационных наблюдений при трех фиксированных значениях наработки В качестве трёх точек выберем t1=0 ч. t2=500 ч. t3=1000 ч.
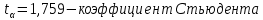
1. Определим коэффициент долговечности А:
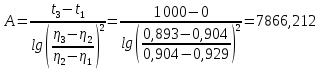
2. Вычислим коэффициент смещения:
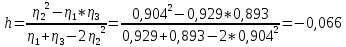
3. Вид функциональной зависимости для мат. ожидания η:
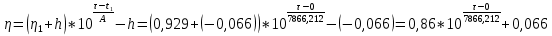
4. Вид функциональной зависимости для верхней доверительной границы
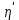
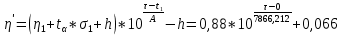
5. Вид функциональной зависимости для верхней доверительной границы
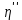
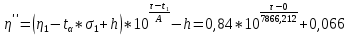
6. Вид функциональной зависимости для скорости изменения параметра V
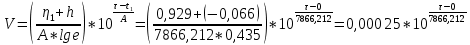
С учетом полученных зависимостей спрогнозируем математическое ожидание, верхний и нижний доверительные пределы, и скорость изменения параметра для времени 
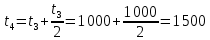
Табл.2.3| t | 0 | 500 | 1000 | 1500 |
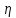| | 0,929 | 1,065 | 1,222 | 1,405 |
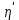| | 0,948 | 1,087 | 1,248 | 1,434 |
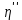| | 0,910 | 1,043 | 1,197 | 1,375 |
| V | 0,000252 | 0,00029224 | 0,000338 | 0,000392 |
Графическое изображение указанных зависимостей представлено на рис. 2.3 и рис.2.4.
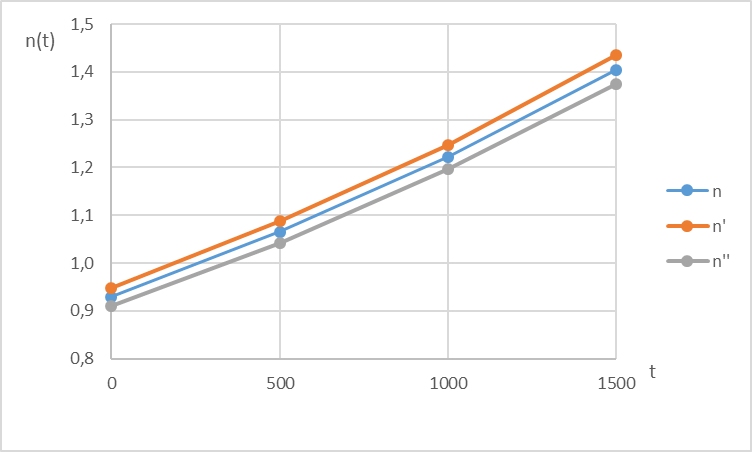
Рис.2.3. Прогноз зависимости параметра от наработки
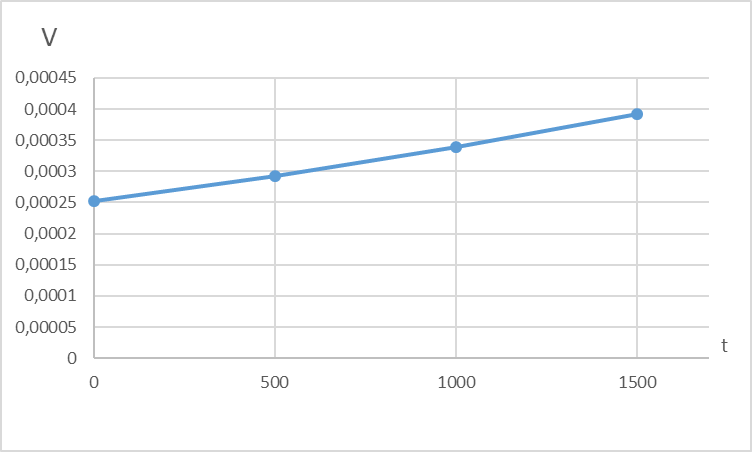
Рис.2.4. Прогноз зависимости скорости изменения параметра от наработки
Вывод по задаче №2: Таким образом мы можем видеть, что прогнозирование параметра по двум точкам для наработки t=1500 ч, дает результат η=0,87, а по трем точкам η=1,405. Результаты расчетов указывают на то, что для более точного прогнозирования необходимо брать как можно большее количество данных о параметре в зависимости от наработки.