Уравнения прямой на плоскости спинодальное

• Название: Уравнения прямой на плоскости спинодальное
• Дата: 08.12.2021
• Размер: 187.25 Kb.
• Имя файла: Mat_otvety_zachet_118.docx
• Тип: Документы; #296706

1.Формула производной :

2.Параметрическое уравнение прямой: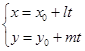

3.Пусть , – точка конечного разрыва I рода, если:

4.Отметить несуществующее название уравнения прямой на плоскости: спинодальное

5.Транспонировать матрицу – значит: элемент с номером ij поместить на место ji

6.Правило Лопиталя Если функции и дифференцируемы в точке , причём , то:

7.Два вектора называются ортогональными, если:их скалярное произведение равно нулю

8. и – две бесконечно малые при функции и называются бесконечно малыми одного порядка при , если:

9.Функция возрастает на отрезке , если на этом отрезке:

10. Выберите функцию, эквивалентную при :

11. Два вектора перпендикулярны тогда и только тогда, когда: их скалярное произведение равно нулю

12.Фокусное расстояние гиперболы:

13.Предел произведения конечного числа функций равен:произведению значений пределов каждой функции в отдельности

14. и – две бесконечно малые при функции и называются эквивалентными при , если:

15.Матричный метод применим для решения системы линейных уравнений, если: матрица системы квадратная и невырожденная

16.Формула производной суммы двух функций

17.Модуль смешанного произведения трех векторов равен: объему параллелепипеда, построенного на этих векторах

18.Длина вектора :

19.Выберите функцию, эквивалентную при :

20.Система имеет единственное решение, если: определитель системы не равен нулю

21.Условие параллельности векторов и :

22.Фокусное расстояние эллипса: если

23.Если функция непрерывна в каждой точке интервала, то она называется:непрерывной в этом интервале

24.Решение системы линейных алгебраических уравнений методом обратной матрицы имеет вид:

25.Выберите функцию, эквивалентную при :

26.При перестановке местами двух столбцов матрицы ее определитель:умножается на (-1)

27.Расстояние от точки до плоскости :

28.Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция в этой точке имеет точку: минимума

29.Метод Крамера применим для решения системы линейных уравнений, если:матрица системы квадратная и невырожденная

30.Формула производной :

31.Дифференциал функции – это:главная часть приращения функции при заданном изменении аргумента

32.Первый замечательный предел:

33.Формула производной

34.Условие параллельности двух прямых, заданных уравнениями с угловыми коэффициентами , :

35.:Предел произведения функций равен:произведению пределов этих функций

36.Дифференциал функции определяется формулой:

37.Квадратная матрица с нулевой строкой имеет определитель равный:0

38. и – две бесконечно малые при функции называется бесконечно малой более высокого порядка если:

39.Уравнение нормали к графику функции в точке :

40.Правила Лопиталя непосредственно применимы для раскрытия неопределенностей вида: и

41.Среди двух неколлинеарных векторов не может быть:нулевого вектора

42.Три вектора образуют правую тройку, если:их смешанное произведение больше нуля

43.Кривая на интервале выпукла вниз, если:

44. и – две бесконечно малые при функции называется бесконечно малой более низкого порядка, чем при , если:

45.Уравнение касательной к графику функции в точке касания :

46.Каноническое уравнение окружности:

47.В точке перегиба графика функции:график меняет характер выпуклости

48.Матрица называется вырожденной, если:определитель квадратной матрицы равен нулю

49.Матрица, в которой число строк равно числу столбцов называется:квадратной

50.Эксцентриситет гиперболы: , если – вещественная полуось

51.Если значения предела функции и самой функции в данной точке равны, то функция в этой точке называется: непрерывной

52.Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является: бесконечно малой величиной

53.Формула производной :

54.Число строк и столбцов определителя называется:порядком определителя

55.Уравнение определяет:параболу

56.Две плоскости в пространстве перпендикулярны, если: их нормальные векторы перпендикулярны

57.Обратная матрица к данной квадратной матрице существует тогда и только тогда, когда:когда определитель матрицы не равен нулю

58.Выберите функцию, эквивалентную при :

59.Формула производной произведения двух функций

60.Функция убывает на отрезке , если на этом отрезке:

61.Выражение называется:приращением функции

62.Если в некоторой точке существуют конечные односторонние пределы функции слева и справа, не равные друг другу, то:это точка разрыва первого рода

63.Система линейных уравнений называется однородной, если ее правая часть:равна нулевому вектору

64.Обратная функция существует для:монотонно убывающей функции

65.Каноническое уравнение прямой в пространстве:

66.Два вектора коллинеарны тогда и только тогда, когда:их векторное произведение равно нулю

67.Расстояние между двумя точками и на плоскости:

68.При умножении двух матриц размерностей и получится матрица размерности:

69.Перемножать можно матрицы:матрицы такие, что левый сомножитель имеет столько столбцов, сколько строк у правого сомножителя

70.Три вектора называются упорядоченной тройкой, если:указано, какой из этих векторов является первым, какой - вторым и какой – третьим

71.Точки, в которых функция не является непрерывной, называются.точками разрыва

72.Выберите функцию, эквивалентную при :

73.Нормальное уравнение плоскости:

74.Выберите правильное утверждение:постоянный множитель можно выносить за знак предела

75.Что означают числа в индексе у элементов матрицы?номер строки и столбца

76.Если функция непрерывна в точке, то:предел в этой точке равен значению функции в ней же

77.Формула производной

78.Формула производной

79.Чтобы вычислить произведение матрицы на число, нужно:умножить каждый элемент на число

80.Длина вектора :

81.Предел постоянной величины равен:постоянной величине

82.Формула производной частного двух функций

83.Кривая на интервале выпукла вверх, если:

84.Асимптоты гиперболы:

85.Формула производной

86.Формула производной разности двух функций

87.Модуль векторного произведения двух векторов равен:площади параллелограмма, построенного на этих векторах

88.Выберите функцию, эквивалентную при :

89.Формула производной

90.Решение системы линейных алгебраических уравнений методом Крамера имеет вид: при :

91.При умножении матрицы на обратную к ней получаем:единичную матрицу

92.Условие перпендикулярности векторов и :

93.Выберите функцию, эквивалентную при :

94. и – две бесконечно малые при функции и называются несравнимыми при , если:

95.Производной функции называется:предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю

96.Что означает запись: размер матрицы 2х4? матрица имеет 2 строки и 4 столбца

97.Уравнение плоскости в отрезках:

98.Какое высказывание является лишним при определении двух равных векторов?описывают одно и то же физическое явление

99.Понятие правой и левой тройки теряет смысл для следующих векторов:компланарных

100.Произведение бесконечно большой и бесконечно малой величин представляет собой:ситуацию неопределенности

101.Три вектора компланарны тогда и только тогда, когда:их смешанное произведение равно нулю

102. Общее уравнение прямой:

103.Выберите неверное утверждение в определении непрерывности функции:функция не определена в точке

104.Эксцентриситет гиперболы:

105.Предел называется:производной

106.Уравнение прямой проходящей через две точки и :

107.Предел суммы конечного числа функций равен: сумме пределов каждой функции в отдельности

108.Функция имеет в точке максимум, если первая производная в этой точке:меняет знак с плюса на минус

109.Отметить несуществующее название уравнения прямой в пространстве:в отрезках

110.Транспонированная квадратная матрица имеет определитель:равный определителю исходной матрицы

111.Метод Гаусса применим для решения системы линейных уравнений, если:матрица системы любая

112.Определитель вычисляется:только для квадратной матрицы

113.Понятие ранга матрицы вводится:для любых матриц

114.Уравнение прямой, проходящей через две данные точки:

115.Функция называется бесконечно малой при , если:

116.Предел частного двух функций равен:частному пределов этих функций

117.Выберите функцию, эквивалентную при :

118.Порядок может быть только у матрицы следующего вида:квадратной