планы7а. Урок 1 Числовые выражения
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
Ход урока I. Организационный момент Устная работа. 1. Какие из чисел 3; –2; 2 являются корнями следующих уравнений: а) 3х = –6; г) 4х – 4 = х + 5; б) 3х + 2 = 10 – х; д) 10х = 5(2х + 3); в) х + 3 = 6; е) 10 + х = 13? 2. Являются ли уравнения равносильными? Если да, то сформулируйте, по какому свойству уравнений. а) 3х + 4 = 2 и 3х = –2; б) –3х + 12 + 2х = 4 и 2х + 12 = 3х + 4; в) 3х + 15 = 0 и 3х = 15; г) 0,5х = 0,08 и 50х = 8; д) 120х = –10 и 12х = 1; е) II. Объяснение нового материала. Рассмотрим уравнение 9х – 23 = 5х – 11. Применим известные свойства уравнений и получим равносильные уравнения: 9х – 5х = – 11 + 23; 4х = 12; х = 3. Уравнение, равносильное исходному, имеет единственный корень 3, значит, исходное уравнение также имеет единственный корень 3. Используя свойства уравнений, многие из них всегда можно привести к виду ax = b, где х – переменная, а a и b – некоторые числа. Уравнения такого вида называются линейными. Важно подчеркнуть учащимся, что, используя буквенные обозначения, мы записали целый класс уравнений. 3. Организация исследовательской деятельности учащихся. На этом этапе востребуется логический прием мышления – обобщение. Задание. Привести уравнение к линейному виду, используя свойства уравнений: а) 3х – 11 = 5х + 7; б) 2 (х + 1) = 2х + 2; в) –8х + 11 = 8 (3 – х). Решение: а) 3х – 11 = 5х + 7; б) 2 (х + 1) = 2х + 2; 3х – 5х = 7 + 11; 2х + 2 = 2х + 2; –2х = 18. 2х – 2х = 2 – 2; 0 · х = 0. в) –8х + 11 = 8 (3 – х); –8х + 11 = 24 – 8х; –8х + 8х = 24 – 11; 0 · х = 13. Теперь, глядя на линейное уравнение, записать, чему равны коэффициенты a и b и сколько корней имеет уравнение. как это определили? а) a = –2; b = 18 – один корень х = –9, определили, разделив обе части на (–2). б) a = 0; b = 0 – бесконечно много корней, так как равенство 0 · х = 0 верно при любом значении х. в) a = 0; b = 13 – нет корней, так как равенство 0 · х = 13 неверно ни при каком значении х. Обобщая полученные данные, заполняем таблицу решения линейного уравнения в общем виде:
4. Создание алгоритма решения уравнений, сводящихся к линейным. Анализируя решенные примеры, приходим к выводу, что решение многих уравнений сводится к решению линейных. Учащиеся могут сами создать алгоритм: 1-й шаг. Если выражения, стоящие в левой или правой части уравнения, содержат скобки, то раскрываем их по правилам. 2-й шаг. Переносим слагаемые с переменными в левую часть уравнения, а без переменных в правую. 3-й шаг. Приводим подобные слагаемые в обеих частях уравнения, приводя его к виду ax = b. 4-й шаг. Решаем получившееся линейное уравнение, равносильное исходному, в зависимости от значений коэффициентов a и b. III. Формирование умений и навыков. Задания, решаемые на этом уроке, направлены на усвоение определения линейного уравнения и решение линейных уравнений в зависимости от значений коэффициентов a и b. 1. (Устно.) Назовите коэффициенты a и b линейного уравнения ax = b. Сколько корней имеет уравнение: а) 3х = 12; в) 1 2. Решите уравнение. а) –8х = 24;г) –3x = в) –18х = 1;е) 3. Определите значение х, при котором значение выражения –3х равно: а) 0; б) 6; в) –12; г) IV. Итоги урока. Домашнее задание: № 126, № 127, № 245, № 142. Урок №14 Линейное уравнение с одной переменной Цель: формировать умение решать по алгоритму уравнения, сводящиеся к линейным. Ход урока I. Организационный момент II. Проверочная работа. Вариант 1 1. Сколько корней имеет уравнение: а) –2х = 17; б) 0 · х = –6; в) 0 · х = 0? 2. Найдите корень уравнения. а) 26х = –78; б) 0,2х = 2,8; в) Вариант 2 1. Сколько корней имеет уравнение: а) 0 · х = –72; б) 2. Найдите корень уравнения. а) 21х = 84; б) –1,2х = 0,36; в) III. Формирование умений и навыков. № 128 (а; б; е; ж; и); № 129; № 131. 3. № 131, № 132. № 131. Решение:
№ 132. Решение: а) (13х – 15) – (9 + 6х) = –3х; 13х – 15 – 9 – 6х = –3х; 13х – 6х + 3х = 15 + 9; 10х = 24; х = 24 : 10; х = 2,4. б) 12 – (4х – 18) = (36 + 4х) + (18 – 6х); 12 – 4х + 18 = 36 + 4х + 18 – 6х; – 4х – 4х + 6х = 36 + 18 – 12 – 18; – 2х = 24; х = 24 : (–2); х = –12. в) 1,6х – (х – 2,8) = (0,2х + 1,5) – 0,7; 1,6х – х + 2,8 = 0,2х + 1,5 – 0,7; 1,6х – х – 0,2х = 1,5 – 0,7 – 2,8; 0,4х = –2; х = (–2) : 0,4; х = –5. г) (0,5х + 1,2) – (3,6 – 4,5х) = (4,8 – 0,3х) + (10,5х + 0,6); 0,5х + 1,2 – 3,6 + 4,5х = 4,8 – 0,3х + 10,5х + 0,6; 0,5х + 4,5х + 0,3х – 10,5х = 4,8 + 0,6 – 1,2 + 3,6; –5,2х = 7,8; х = 7,8 : (–5,2); х = –1,5. 4. № 134. Решение:
5. При каком значении t: а) значение выражения 5t + 11 равно значению выражения 7t + 31; б) значение выражения 8t + 3 в три раза больше значения выражения 5t – 6; в) значение выражения 5t + 1 в два раза меньше значения выражения 10t + 18; г) значение выражения 0,25t – 31 на 5 больше значения выражения д) значение выражения 13t – 7 на 8 меньше значения выражения 12t + 11; е) разность выражений 1,5t – 37 и 1,5t – 73 равна 36? Основную трудность при составлении равенств у учащихся вызывают задания б) – д). Следует разобрать принцип составления равенства с использованием наглядности. Решение: б) 8t + 3 5t – 6 8t + 3 3 (5t – 6)  (8t + 3) = 3 (5t – 6); 8t + 3 = 15t – 18; 8t – 15t = – 18 – 3; –7t = –21; t = 3. в) 5t + 1 10t + 18 5t + 1 (10t + 18) : 2 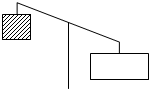 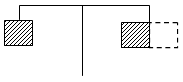 5t + 1 = (10t + 18) : 2; 5t + 1 = 5t + 9; 5t – 5t = 9 – 1; 0 · t = 8 – нет решений. г) 0,25t – 31  + 5 + 5 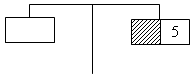 0,25t – 31 = 0,25t – 0 · t = 18 – нет решений. д) 13t – 7 = (12t + 11) – 8 или (13t – 7) + 8 = 12t + 11. е) (1,5t – 37) – (1,5t – 73) = 36; 1,5t – 37 – 1,5t + 73 = 36; 1,5t – 1,5t = 36 + 37 – 73; 0 · t = 0 – t – любое число. IV. Итоги урока. Домашнее задание: № 128 (в; г; д; з); № 130; № 133; № 135. Урок №15 Линейное уравнение с одной переменной Цели: продолжить формировать умение решать уравнения, сводящиеся к линейным. Ход урока I. Организационный момент Устная работа. 1. Показать, что следующие уравнения не имеют решений, и объяснить почему: а) х + 3 = х; в) 2х = 2(х + 1); д) (–х)2 + 1 = 0. б) х – 1 = х + 1; г) х2 + 4 = 0; 2. Определить, равносильны ли уравнения и почему: а) 5х + 1 = 2 и 10х + 2 = 4; б) 2х – 1 = 4 и 2х = 6; в) 3х + 1 = 10 и х = 3; г) 2х + 3 = 2х – 4 и х + 5 = х; д) II. Математический диктант. Вариант 1 1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным х. 2. Как называется уравнение –2х = 17? 3. При каком условии уравнение сх = 5 имеет единственный корень? Запишите этот корень. 4. Решите уравнение 0,2х = –1. 5. К обеим частям уравнения прибавили число –3. Какими являются полученное и исходное уравнения? 6. Решите уравнение 2х + 1 = 3х – х. 7. Решите уравнение 5 – х = 2х + 2. Вариант 2 1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным у. 2. Как называется уравнение 17х = –2? 3. При каком условии уравнение ау = 3 не имеет корней? 4. Решите уравнение –0,3х = 1. 5. Обе части уравнения умножим на число –7. Какими являются полученное и исходное уравнения? 6. Решите уравнение х + 3 = 5 + х – 2. 7. Решите уравнение 2 – 2х = –2х + 3. III. Формирование умений и навыков. 1. Решите уравнение. а) (5х – 3) + (7х – 4) = 8 – (15 – 11х); б) (4х + 3) – (10х + 11) = 7 + (13 – 4х); в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8; г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х. Решение: а) (5х – 3) + (7х – 4) = 8 – (15 – 11х); 5х – 3 + 7х – 4 = 8 – 15 + 11х; 5х + 7х – 11х = 8 – 15 + 3 + 4; х = 0. б) (4х + 3) – (10х + 11) = 7 + (13 – 4х); 4х + 3 – 10х – 11 = 7 + 13 – 4х; 4х – 10х + 4х = 7 + 13 – 3 + 11; –2х = 28; х = 28 : (–2); х = –14. в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8; 7 – 5х – 8 + 4х + 5х + 6 = 8; – 5х + 4х + 5х = 8 – 7 + 8 – 6; 4х = 3; х = г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х; 3 – 2х + 4 – 3х + 5 – 5х = 12 + 7х; – 2х – 3х – 5х – 7х = 12 – 3 – 4 – 5; –17х = 0; х = 0. 2. Среди данных уравнений выберите те, которые имеют тот же корень, что и уравнение 2х – 3 = 5х + 6: а) 19 (2х – 3) = 19 (5х + 6); б) 5х – 2х = 6 – 3; в) Решение: 2х – 3 = 5х + 6; 2х – 5х = 6 + 3; –3х = 9; х = –3. а) 19 (2х – 3) = 19 (5х + 6); | : 19 2х – 3 = 5х + 6; х = –3, так как уравнение равносильно исходному. При решении данного уравнения важно заметить, что разделить обе части уравнения на 19 рационально, а выполнить умножение числа на скобку – нет. б) 5х – 2х = 6 – 3; в) 3х = 3; 2х – 3 = 5х + 6; х = 1. 2х – 5х = 6 + 3; х = –3, так как уравнение равносильно исходному. Ответ: а); в); х = –3. 3. Среди данных уравнений укажите те, которые не имеют корней: а) 5х – 10 = 4х; в) 5 – х = 6 – х; д) | x | + 1 = 0. б) 3х + 7 = 3х + 11; г) | x | = 8; Решение: а) 5х – 10 = 4х; б) 3х + 7 = 3х + 11; 5х – 4х = 10; 3х – 3х = 11 – 7; х = 10. 0 · х = 4 – нет корней. в) 5 – х = 6 – х; г) | x | = 8; д) | x | + 1 = 0. –х + х = 6 – 5; х = 8 или х = –8. | x | = –1 – 0 · х = 1 – нет корней. нет решений, так как | x | ≥ 0. № 238. Решение: Если т 0, то тх = 5 имеет единственный корень х = 5 : т. Если т = 0, то уравнение примет вид 0 · х = 5, оно не имеет корней. Не существует такое значение т, чтобы уравнение имело бесконечно много корней. № 239. Решение: Если х = –5, то р · (–5) = 10 – верное равенство. Найдем р: р = 10 : (–5); р = –2. Если х = 1, то р · (–1) = 10; р = 10 : (–1); р = –10. Если х = 20, то р · 20 = 10; р = 10 : 20; р = 0,5. Ответ: –2; –10; 0,5. Обращаем внимание учащихся, что это уравнение с параметром р. № 242. Решение: а) (х + 5) (х + 6) + 9 = 0; х2 + 6х + 5х + 30 + 9 = 0; х2 + 11х + 39 = 0; х2 = –11х – 39. Слева стоит выражение, значение которого не отрицательно. если х – положительное число, то –11х < 0 и –11х – 39 < 0, значит, х2 = –11х – 39 – неверно для любого положительного х, значит, уравнение не может иметь положительный корень. б) х2 + 3х + 1 = 0. Если х > 0, то каждое слагаемое в левой части уравнения положительно, значит, и вся сумма положительна, следовательно, х > 0 не может являться корнем данного уравнения. |
