планы7а. Урок 1 Числовые выражения

Название	Урок 1 Числовые выражения
Дата	20.04.2022
Размер	2.05 Mb.
Формат файла
Имя файла	планы7а.doc
Тип	Урок #486320
страница	7 из 26

1 2 3 4 5 6 7 8 9 10 ... 26

IV. Итоги урока.

Домашнее задание: № 136, № 137, № 138

Урок №16
Решение задач с помощью уравнений

Цели: обеспечить понимание уравнения в качестве математической модели некоторой жизненной ситуации, описанной в текстовой задаче; выделить этапы решения задач алгебраическим методом; формировать умение составлять уравнение по условию задачи и решать его.

Ход урока

I. Организационный момент

II. Объяснение нового материала.

1. Объяснение начать с решения конкретной (приведенной в учебнике) задачи № 1.

Можно воспользоваться таблицей: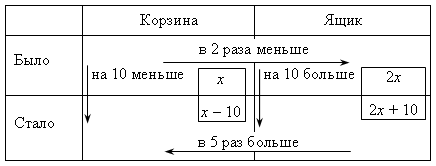

Сперва в таблице стрелками обозначаем и подписываем все зависимости, затем видим, что неизвестны все четыре клеточки, значит, обозначить переменной удобно главный вопрос задачи, например, количество яблок в корзине первоначально. Затем, по стрелкам, заполняем все клеточки. Последняя стрелка даст уравнение: 5(х – 10) = 2х + 10.

Аналогичную таблицу можно составить для задачи № 2: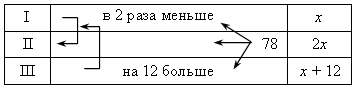

х + 2х + (х + 12) = 78.

При решении второй задачи особое внимание уделяется последнему этапу – интерпретации полученного результата.

III. Формирование умений и навыков.

1. № 143.

Решение:

Пусть в одной кассе было х билетов, тогда во второй – (х + 36) билетов. Зная, что всего было продано 392 билета, составим уравнение:

х + (х + 36) = 392;

х + х + 36 = 392;

2х = 356;

х = 178.

Следовательно, в первой кассе было продано 178 билетов.

Так как х + 36 = 178 + 36 = 214, то во второй кассе было продано 214 билетов.

Ответ: 178 и 214 билетов.

2. № 146.

Решение:

Анализ условия: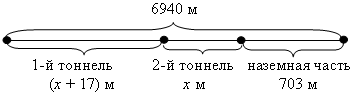

Пусть х м – длина одного тоннеля, тогда (х + 17) м – длина другого. Так как наземная часть составляет 703 м, а вся трасса – 6940 м, то длина тоннелей в сумме составляет (6940 – 703) м. Зная, что длина тоннелей равна х + (х + 17) м, составим уравнение:

х + (х + 17) = 6940 – 703;

х + х + 17 = 6237;

х + х = 6237 – 17;

2х = 6220;

х = 3110.

Значит, длина одного тоннеля равна 3110 м. Так как х + 17 = = 3110 + 17 = 3127, то длина другого тоннеля равна 3127 м.

Ответ: 3110 м и 3127 м.

3. № 147.

Анализ условия: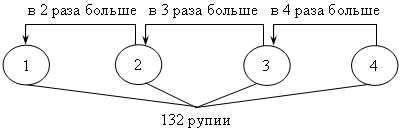

Пусть первый жертвователь дал х рупий, тогда второй дал 2х рупий, третий – 3 · 2х рупий, четвертый – 4 · (3 · 2х) рупий. Зная, что все вместе они дали 132 рупии, составим уравнение:

х + 2х + 3 · 2х + 4 · (3 · 2х) = 132;

х + 2х + 6х + 24х = 132;

33х = 132;

х = 132 : 33;

х = 4.

Значит, первый жертвователь дал 4 рупии. Так как 2х = 2 · 4 = 8, то второй дал 8 рупий. Так как 3 · 2х = 3 · 8 = 24, то третий дал 24 рупии. Так как 4 · (3 · 2х) = 4 · 24 = 96, то четвертый дал 96 рупий.

Ответ: 4; 8; 24 и 96 рупий.

4. № 148.

Анализ условия: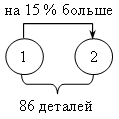

Пусть х деталей изготовил второй рабочий, тогда первый изготовил (х + 0,15х) деталей. Зная, что вместе они изготовили 86 деталей, составим уравнение:

х + (х + 0,15х) = 86;

х + х + 0,15х = 86;

2,15х = 86;

х = 86 : 2,15;

х = 40.

Значит, второй рабочий изготовил 40 деталей. Так как х + 0,15х = 40 +
+ 0,15 · 40 = 40 + 6 = 46, то первый рабочий изготовил 46 деталей.

Ответ: 46 деталей и 40 деталей.

IV. Итоги урока.

Домашнее задание: № 144; № 145; № 149; № 165.

Урок 18
Решение задач с помощью уравнений

Цели: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.

Ход урока

I. Устная работа.

1. Вычислите.

а) 0,35 · 0,2 + 0,35 · 0,8; в)

; д)

;б)

· 0,5 · 8; г)

; е) (–3)² – 9,2.

2. Выразите:

а) t из s = υ · t; в) y из υ = 2a – y;

б) p из N = p : t; г) x из y =

.

II. Проверочная работа.

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

III. Формирование умений и навыков.

При решении задач замечаем, что неизвестную величину не обязательно обозначаем за х. Наоборот, если в задаче используется формула, например, s = υ · t, то и переменную удобно обозначать соответствующей буквой.

1. № 151.

Решение: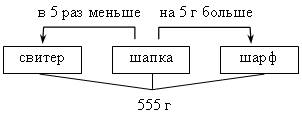

Пусть х г шерсти ушло на шапку, тогда на свитер ушло 5х г, а на шарф – (х – 5) г шерсти. Зная, что на все изделия ушло 555 г шерсти, составим уравнение:

х + 5х + (х – 5) = 555;

х + 5х + х – 5 = 555;

7х = 560;

х = 80.

Значит, на шапку ушло 80 г шерсти. Так как 5х = 5 · 80 = 400, то на свитер ушло 400 г шерсти.

Так как х – 5 = 80 – 5 = 75, то на шарф ушло 75 г шерсти.

Ответ: 400 г; 80 г; 75 г.

2. № 152.

Решение: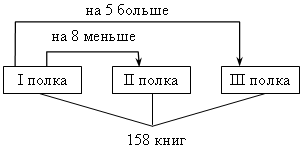

Пусть на первой полке расположено п книг, тогда на второй полке – (п + 8), а на третьей – (п – 5) книг. Зная, что на трех полках необходимо расположить всего 158 книг, составим уравнение:

п + (п + 8) + (п – 5) = 158;

п + п + 8 + п – 5 = 158;

3п + 3 = 158;

3п = 155;

п = 51

.

Интерпретация результата: так как п – число книг, то п дол-жно быть натуральным числом. 51

– дробное, значит, указанным способом нельзя разместить книги на полках.

Ответ: нельзя.

На примере этой задачи видно, что важен этап интерпретации полученного решения.

3. № 154.

Решение: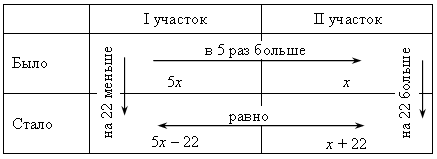

Пусть х кустов малины было на втором садовом участке, тогда на первом было 5х кустов. После пересадки на первом участке осталось (5х – 22) кустов малины, а на втором стало (х + 22) куста малины. Зная, что после пересадки на обоих участках стало кустов малины поровну, составим уравнение:

5х – 22 = х + 22;

5х – х = 22 + 22;

4х = 44;

х = 11.

Значит, на втором участке было 11 кустов малины. Так как 5х =
= 5 · 11 = 55, то на первом участке было 55 кустов малины.

Ответ: 55 и 11 кустов малины.

4. № 155.

Решение:

Анализ условия:

	υ (км/ч)	t (ч)	s (км)
По течению	υ_c + 2	9	9 · (υ_c + 2)
Против течения	υ_c – 2	11	11 · (υ_c – 2)

Пусть υ_c км/ч – собственная скорость теплохода, тогда по течению он шел со скоростью (υ_c + 2) км/ч и за 9 часов прошел 9 · (υ_c + 2) км. Против течения он шел со скоростью (υ_c – 2) км/ч и прошел 11 · (υ_c – 2) км. Зная, что он прошел по течению и против одинаковое расстояние, составим уравнение:

9 · (υ_c + 2) = 11 · (υ_c – 2);

9υ_c + 18 = 11υ_c – 22;

9υ_c – 11υ_c = – 22 – 18;

–2υ_c = –40;

υ_c = 20.

Значит, собственная скорость теплохода равна 20 км/ч.

Ответ: 20 км/ч.

При обозначении переменной можно не ставить индекс υ_c, а просто обозначить υ. Не возбраняется использовать любую букву латинского алфавита.

5. № 157.

Решение:

	υ (верст/день)	t (день)		s (верст)
I	40		п + 1		40 (п + 1)
II	45		п		45п

Пусть второй человек догонит первого через п дней, тогда за эти дни он пройдет 45п верст. Первый человек, так как он шел на день дольше, пройдет 40 (п + 1) верст. Зная, что они пройдут одинаковое расстояние, составим уравнение:

45п = 40 (п + 1);

45п = 40п + 40;

45п – 40п = 40;

5п = 40;

п = 8 Значит, через 8 дней второй догонит первого.

IV. Итоги урока.

Домашнее задание: № 150, № 153, № 156, № 248.

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

Урок №19
Решение задач с помощью уравнений

Цель: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.

1 2 3 4 5 6 7 8 9 10 ... 26