планы7а. Урок 1 Числовые выражения
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
IV. Итоги урока. – Что называется функцией? – Что называется аргументом? – Какими способами можно задать функцию? Назовите преимущества каждого из них. Домашнее задание: 1. № 259; № 262; № 264. 2. Функция задана графиком:  а) Найти значения функции при значениях аргумента 0; –2; 1; 3. б) При каком значении х значение функции равно 2; 0; 1; –1? в) Назвать несколько значений х, при которых значение функции положительно. г) Назвать несколько значений х, при которых значение функции отрицательно. Урок 26 Вычисление значений функции по формуле Цели: продолжить работу по усвоению понятия функции и связанных с функцией понятий (область определения функции, область значений функции и др.); формировать умение находить значения функций, заданных аналитически (с помощью формулы). Ход урока I.Организационный момент Устная работа. 1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа; сумму этого числа с числом 5. 2. Велосипедист едет со скоростью 15 км/ч и за t ч проходит расстояние s км (зависимость s от t). Найдите значение функции, соответствующее значению аргумента, равному II. Объяснение нового материала. Цель этого и последующих занятий – в упорядочении имеющихся представлений о функции, развертывании системы понятий, характерных для функциональной линии. Значительное место должно быть отведено усвоению важного представления – однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции. Чаще других в математике и её приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Однако сопоставление разных способов задания выполняет важную роль: 1) и таблицы, и графики служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи; 2) необходимо для усвоения всего многообразия аспектов понятия функции. Объяснение проводить согласно пункту 13 учебника. Разбираем пример № 1 со с. 55 учебника. Показываем, что для того, чтобы найти значение функции, необходимо подставить некоторое значение аргумента в формулу. Также объясняем, что в случае, когда область определения функции явно не задана, считают, что она состоит из всех значений независимой переменной, при которых эта формула имеет смысл. III. Формирование умений и навыков. 1. № 267. 2. Вычислить значение следующих функций при х, равном –2; –1; 0; 1; 2. а) у = 3х; б) у = –2х; в) у = –х – 3; г) у = 20х + 4. 2-я группа. 1. № 270. 2. № 271.Решение: у = х (х – 3,5)
1. Найдите область определения функции, заданной формулой: а) у = 3х + 2; б) у = г) у = 2. № 351.Решение: а) у = Область определения функции – все числа, кроме тех, при которых х – 4 = 0, то есть х2 = 4. Значит, не входят в ООФ х = 2 и х = –2. б) у = Область определения функции – все числа, кроме тех, при которых х2 + 4 = 0, то есть х2 = –4. Уравнение не имеет решения, значит, ООФ – любое число. Ответ: а) любое число, кроме 2 и –2; б) любое число. 3. Дополнительные задания (для сильных учащихся). 3.1. Найдите область определения функции. а) у =  б) у =  3.2. Задайте формулой какую-нибудь функцию, область определения которой: а) все действительные числа; б) все действительные числа, кроме –11; в) все действительные числа, кроме 3 и 5; г) все неотрицательные действительные числа; д) все неположительные действительные числа.; е) только одно число. IV. Проверочная работа. Вариант 1 1. Дана функция у = 2х2 – 4х. Найдите значение функции при х = 0 и х = –1. 2. Найдите область определения функции. а) у = 2х – 7; б) у = Вариант 2 1. Дана функция у = 5х2 + х. Найдите значение функции при х = 0 и х = 1. 2. Найдите область определения функции. а) у = 3х + 6; б) у = V. Итоги урока. Домашнее задание: 1. № 268; № 269; № 272. Урок 27 Вычисление значений функции по формуле Цели: продолжить формировать умение находить значение функции по формуле, а также формировать умение находить значение аргумента, соответствующее заданному значению функцию, умение решать практические задачи с использованием функциональной терминологии. Ход урока I. Организационный момент Устная работа. 1. Найдите значение функции у = 2х – 1 для значений аргумента, равного 0; 1; 2; –1. 2. Найдите область определения функции: а) у = 3х – 7; б) у = II. Формирование умений и навыков. 1. № 273, № 274. 2. Функция задана формулой у = 2х – 1. а) Какое значение у соответствует х, равному 10; –4,5; 15; 251; 600? б) При каком значении х соответствующее значение у равно: –19; –57; 205; –3 Решение: а) Если х = 10, то у = 2 · 10 – 1 = 19; если х = –4,5, то у = 2 · (–4,5) – 1 = –10; если х = 15, то у = 2 · 15 – 1 = 29; если х = 251, то у = 2 · 251 – 1 = 501; если х = 600, то у = 2 · 600 – 1 = 1199. б) Если у = –19, то 2х – 1 = –19; 2х = –19 + 1; 2х = –18; х = –9; то есть у = –19, при х = –9. Если у = –57, то 2х – 1 = –57; 2х = –57 + 1; 2х = –56; х = – 28, то есть у = –57 при х = – 28. Если у = 205, то 2х – 1 = 205; 2х = 205 + 1; 2х = 206; х = 103, то есть у = 205 при х = 103. Если у = –3 2х = –3,5 + 1; 2х = –2,5; х = –1,25, то есть у = –3 1. Из формулы равномерного движения s = υt выразить скорость υ как функцию пути s и времени t. Вычислить по этой формуле среднюю скорость полета пули, если s = 3 км, t = 6 с. 2. № 276.Решение: Обозначим за т массу пробки в граммах, а за V – объем в см3. Тогда зависимость массы куска пробки от объема можно выразить формулой т = 0,18 · V. а) Если V = 240, то т = 0,18 · 240 = 43,2 (г); б) если т = 64,8, то 0,18 · V = 64,18; V = 64,18 : 0,18; V = 360 (см3). Ответ: а) 43,2 г; б) 360 см3. 3. № 278.Решение: Анализ условия:  s = 12 · t. а) Если t = 3,5, то s = 12 · 3,5 = 42 (км); б) если s = 30, то 12 · t = 30; t = 30 : 12; t = 2,5 (ч). Ответ: а) 42 км; б) 2,5 ч. 4. № 352.Решение: Анализ условия: у = 1,5х + 150. а) если х = 10, то у = 1,5 · 10 + 150 = 15 + 150 = 165; б) если у = 180, то 1,5х + 150 = 180; 1,5х = 180 – 150; 1,5х = 30; х = 30 : 1,5; х = 20, значит, у = 180 при х = 20. Ответ: а) у = 165; б) х = 20. III. Проверочная работа. Вариант 1 1. Функция задана формулой у = 3х – 7. Найдите значение аргумента, при котором значение функции равно нулю. 2. Найдите значение аргумента, при котором функция у = –3х – 2 принимает значение 0,3. 3. Запишите область определения функции, заданной формулой у = Вариант 2 1. Функция задана формулой у = 5 + 2х. Найдите значение аргумента, при котором значение функции равно нулю. 2. Найдите значение аргумента, при котором функция у = –5х + 11 принимает значение 0,2. 3. Запишите область определения функции, заданной формулой у = IV. Итоги урока. – Дайте определение функции. Что называется аргументом, значением функции? – Объясните на примере функции, заданной формулой у = 3х + 18 Домашнее задание: № 275; № 277; № 279; № 353. Урок 28 График функции. Цели: формировать понятие «график функции», умение строить график функции, заданной аналитически, а также с помощью графика находить значение функции, соответствующее заданному значению аргумента, и значения аргумента, которым соответствует данное значение функции. Ход урока I. Проверочная работа. Вариант 1 1. Найдите значения функции, заданной формулой у = 2. Найдите значение аргумента, при котором функция у = 4х + 3 принимает значение, равное Вариант 2 1. Найдите значения функции, заданной формулой у = 2. Найдите значение аргумента, при котором функция у = 5х + 4 принимает значение, равное 1,5. II. Устная работа. На рисунке изображен график зависимости некоторой величины у от некоторой величины х. 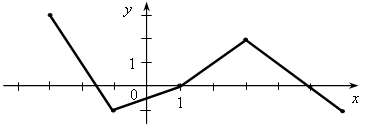 Ответьте на вопросы: а) Чему равное значение у, если х = –3; –1; 2; 5? б) Чему равны значения х, если у = 3; 0; 1? в) Какое минимальное и какое максимальное значения принимает величина у? III. Объяснение нового материала. На этом уроке наша задача – показать, что эти два способа тесно связаны с графическим, причем его особенность в том, что с помощью графика мы можем наглядно представлять функциональную зависимость не только для точечной, но и бесконечной области определения функции:
В соответствии с этими положениями объяснение нового материала проводится в несколько этапов: 1) Формирование представления о графике функции на основе связи аналитического, табличного и графического способов задания функции. 2) введение определения понятия графика функции. 3) Построение графика функции по точкам. 4) Работа по изображенному графику функции. На рисунке изображены точки на координатной плоскости, выражающие результаты наблюдений за атмосферным давлением. Построить график зависимости давления от времени в промежутке 12 ≤ t ≤ 18, соединив эти точки плавной линией.  Затем рассматриваем пример со с. 58 учебника, в котором показано, как по точкам строится график функции y = Необходимо сделать вывод: по точкам можно построить график любой функции, заданной таблично или аналитически (с помощью формулы). Вводим определение:
На примере 2 со с. 60 учебника показываем работу по изображенному графику на нахождение значения функции по заданному значению аргумента и обратное задание. IV. Формирование умений и навыков. 1. № 283. Можно задать учащимся дополнительные вопросы: а) Сколько точек пересечения с осью х имеет график? Каково значение у в этих точках? б) Сколько точек пересечения с осью у имеет график? Каково значение х в этой точке? в) Сравните значения функции в точках –2 и 1. г) Назовите координаты какой-нибудь точки графика, у которой значения аргумента и функции положительны; значение аргумента положительно, а функции – отрицательно и т. д. 2. № 284, № 285. 3. Используя график функции, заполните таблицу значений функции для –2 ≤ х ≤ 3 с шагом 0,5.  |
