планы7а. Урок 1 Числовые выражения
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
Ход урока I. Устная работа. 1. Найдите область определения функции. а) y = 3x + 2; б) y =  ;г) y = ;г) y = 2. Является ли функция прямой пропорциональностью: а) y = 182x;б) y = 3. Функция задана формулой у = kх. Найдите коэффициент прямой пропорциональности k, если: а) х = 2; у = 4; б) x = II. Объяснение нового материала. Начинаем с рассмотрения конкретной функции (см. учебник, с. 66). Можно предложить учащимся лабораторную работу: подобрать функции, заданные формулами: у = 0,5х; у = –0,5х; у = х; у = –х; у = 1,5х; у = –1,5х; у = 2х; у = –2х; у = 2,5х; у = –2,5х; у = 3х; у = –3х; у = 3,5х; у = –3,5х; у = 4х; у = –4х. Затем заполнить таблицу значений функции при –4 ≤ х ≤ 4 с шагом 0,5. выводы: 1) График прямой пропорциональности является прямой, проходящей через начало координат. 2) Если коэффициент пропорциональности k > 0, то график расположен в первой и третьей координатных четвертях. 3) Если коэффициент пропорциональности k < 0, то график расположен во второй и четвертой координатных четвертях. На основе этих выводов учащиеся выводят простейший алгоритм построения графика прямой пропорциональности: 1-й шаг. Для х1 0 вычислить у1 по формуле у = kх. 2-й шаг. Отметить в координатной плоскости точки с координатами (0; 0) и (х1; у1). 3-й шаг. Провести прямую через построенные точки. III. Формирование умений и навыков. Упражнения, выполняемые на этом уроке, направлены на отработку алгоритма построения графика прямой пропорциональности и нахождения значений функции по графику. 1. № 300, № 302. № 302.
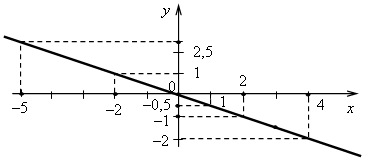
Пусть х = 3, тогда у = –0,5 · 3 = –1,5. Проведем прямую, проходящую через начало координат и точку с координатами (3; –1,5). а) Если х = –2, то у = 1; б) у = –1 при х = 2; если х = 4, то у = –2; у = 0 при х = 0; если х = 1, то у = –0,5. у = 2,5 при х = –5. Если у = –150, то найдем х, решив уравнение: –0,5х = –150; х = –150 : (–0,5); х = 300. При выполнении этого задания повторяем с учащимися правило нахождения по графику значения функции по данному значению аргумента и наоборот (отмечаем точку на оси абсцисс; проводим прямую, перпендикулярную оси абсцисс, до пересечения с графиком функции; из полученной точки опускаем перпендикуляр на ось ординат и находим соответствующее числовое значение ординаты). Также на этом примере показываем, что очень важен выбор правильной величины единичного отрезка. Если взять в качестве единицы измерения одну клеточку, то будет очень неудобно строить график, точки будут «слипаться», чертеж будет грязным и нефункциональным. При больших значениях аргумента или функции (у = –150) удобнее работать с формулой и выполнять действия аналитически (решить уравнение; вычислить по формуле). 2. № 303 (устно). Выполняем работу по предыдущему чертежу. 3. № 305, № 306.
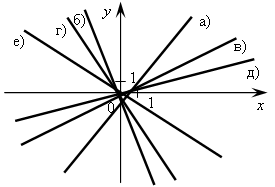
После выполнения этого задания обсудить с учащимися, почему график а) расположен в первой четверти выше графика в). № 306. Решение: Все графики являются прямыми, проходящими через начало координат, значит, функции являются прямыми пропорциональностями и их можно задать формулой у = kх. Задача сводится к нахождению коэффициента k. Выберем на каждом графике произвольную точку с целыми координатами: I (2; 6), значит, 6 = k · 2; k = 3; у = 3х; II (4; 1), значит, 1 = k · 4; k = 0,25; у = 0,25х; III (2; –2), значит, –2 = k · 2; k = –1; у = –х; IV (2; –6), значит, –6 = k · 2; k = –3; у = –3х. Ответ: у = 3х; у = 0,25х; у = –х; у = –3х. IV. Проверочная работа. Вариант 1 1. График функции у = kх проходит через точку В (–30; 3). Найдите k. 2. Построить графики функций: а) у = 5х; б) у = –5х. В каждом случае указать координаты двух точек графика, лежащих выше оси абсцисс. Вариант 2 1. График функции у = kх проходит через точку А (4; –80). Найдите k. 2. Построить графики функций: а) у = 6х; б) у = –6х. В каждом случае указать координаты двух точек графика, лежащих ниже оси абсцисс. V. Итоги урока. Домашнее задание: 1. № 301; № 304. № 357. Урок 31 линейная функция и её график Цели: ввести понятие линейной функции; формировать умение выделять линейную функцию из множества функций; определить график линейной функции и выявить роль параметров k и b в расположении графика линейной функции. Ход урока I. Устная работа. 1. Какие из функций являются прямой пропорциональностью: а) у = 13х; б) у =  ? ?2. Какая из точек принадлежит графику функции, заданной формулой у = а) (0; –2); б) г) (0; 0); д) 3. График линейной пропорциональности проходит через точку А. Найдите коэффициент пропорциональности, если: а) А  ; ;г) А II. Объяснение нового материала. Весь материал целесообразно разбить на несколько логических частей и на каждом уроке изучать одну из них. На этом уроке целесообразно рассмотреть два вопроса: понятие линейной функции и влияние параметров k и b на расположение графика линейной функции. В соответствии с этим объяснение проводится в два этапа. 1. Введение понятия линейной функции. Понятие линейной функции начинаем изучать с рассмотрения реальных процессов и реальных ситуаций. Необходимо привести примеры из учебника и вынести полученные формулы на доску: s = 50t + 20, где t ≥ 0; y = 3x + 5, где x N. Далее можно спросить учащихся: что общего во всех этих формулах? Затем сообщить им, что зависимости такого вида называются линейными функциями, и дать четкое определение. На доску может быть вынесена запись:
2. Определение прямой пропорциональности как частного случая линейной функции. Обращаем внимание учащихся, что в отличие от определения прямой пропорциональности, где k 0, в формуле линейной функции коэффициенты k и b – любые числа, то есть могут равняться нулю. Причем как по отдельности, так и одновременно. В случае если k 0 и b = 0, функция у = kx + b принимает вид у = kx, то есть является прямой пропорциональностью. Сразу делаем вывод: графиком линейной функции в этом случае является прямая, проходящая через начало координат, и для её построения необходимо вычислить по формуле координаты ещё одной точки. 3. График линейной функции и роль параметров k и b в её расположении. а) Следующим шагом целесообразно рассмотреть случай k 0 и b 0. Заполняем таблицу со с. 71 учебника для функций у = 0,5х и у = 0,5х + 2. Анализируя полученные данные, учащиеся делают вывод: графиком функции у = 0,5х + 2 является прямая, параллельная прямой, являющейся графиком функции у = 0,5х, и любая точка графика получается сдвигом по оси у на 2 единицы вверх. Устное упражнение. Что является графиком функции у = 3х + 1; у = –1,5х + 2; у = 2х – 14; у = –3х – 1,5? б) Рассматриваем случай k = 0, b 0. Функция у = kx + b принимает вид у = b. Получаем, что, независимо от значения х, у всегда равно b. Значит, графиком функции является прямая, параллельная оси х и проходящая через точку (0; b). в) Рассматриваем случай k = 0, b = 0. Функция у = kx + b принимает вид у = 0, то есть графиком является сама ось х. После этого на доску можно вынести запись:
4. Последним шагом формулируем простейший алгоритм построения графика линейной функции: 1-й шаг. По формуле найти координаты двух точек графика. 2-й шаг. Отметить полученные точки на координатной плоскости. 3-й шаг. Провести через построенные точки прямую. III. Формирование умений и навыков. 1. Рассматриваем примеры 3–5 со с. 72–73 учебника. Во время работы учащиеся должны называть значения коэффициентов k и b. 2. Определите, какие из следующих функций являются линейными. Назовите для них значения коэффициентов k и b. а) у = 2,5x – 7; б) у = 4 – г) у = ж) у = 3x2 + 2; з) у = –5; и) у = 0. 3. Что является графиком линейной функции и как он расположен? а) у = –3x + 5; б) у = г) у = 4. На рисунках изображены графики функций. Какие из этих функций являются линейными? а) 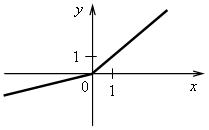 в) в) 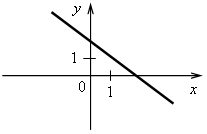 б) б) 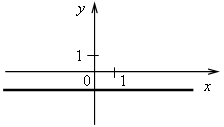 г) г) 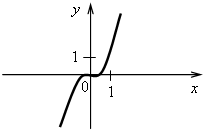 5. № 313, 315. 6. № 319, 321. IV. Итоги урока. Домашнее задание: № 314; № 316 (устно); № 318; № 320. Урок 35 Взаимное расположение графиков линейных функций Цели: продолжить формировать умение строить график линейной функции и определять по графику значение функции по данному аргументу и наоборот; ввести понятие углового коэффициента прямой и выявить случаи взаимного расположения графиков линейных функций в зависимости от значений угловых коэффициентов. Ход урока I. Организационный момент II. Проверочная работа. Вариант 1 1. Постройте график функции, заданной формулой у = –2х+ 0,5. 2. Линейная функция задана формулой у = 5х – 12. Найдите: а) значение у, если х = 1,2; –3; б) значение х, при котором у = 0; –1,5. Вариант 2 1. Постройте график функции, заданной формулой у = –3х– 1,5. 2. Линейная функция задана формулой у = –4х + 7. Найдите: а) значение у, если х = –1,3; 8; б) значение х, при котором у = –2,8; 0. III. Актуализация знаний. 1. Назовите координаты точек пересечения графиков функций с осями координат. Какие особенности этих точек? а) 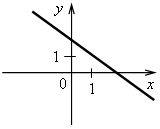 б) б)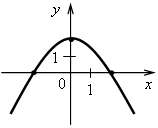 в) в)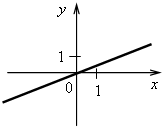 г) г) 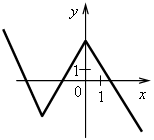 д) д)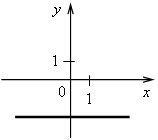 е) е) 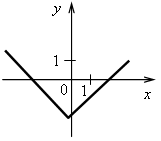 2. № 322, № 324. № 322. Решение: а) у = –2,4х + 9,6. Точка пересечения с осью х имеет ординату, равную нулю. Найдем её абсциссу, решив уравнение: –2,4х + 9,6 = 0; –2,4х = – 9,6; х = – 9,6 : (–2,4); х = 4. (4; 0) – точка пересечения с осью х. Точка пересечения с осью у имеет абсциссу, равную нулю. Найдем её ординату по формуле: Если х = 0, то у = –2,4 · 0 + 9,6 = 9,6. (0; 9,6) – точка пересечения с осью у. б) у = –0,7х – 28. Если у = 0, то –0,7х – 28 = 0; –0,7х = 28; х = 28 : (–0,7); х = –40. (–40; 0). Если х = 0, то у = –0,7 · 0 – 28 = –28. (0; –28). в) у = 1,2х + 6. Если у = 0, то 1,2х + 6 = 0; 1,2х = –6; х = –6 : 1,2; х = –5. (–5; 0). Если х = 0, то у = 1,2 · 0 + 6 = 6. (0; 6). г) у = –5х + 2. Если у = 0, то –5х + 2 = 0; –5х = –2; х = –2 : (–5); х = 0,4. (0,4; 0). Если х = 0, то у = –5 · 0 + 2 = 2. (0; 2). Ответ: а) (4; 0), (0; 9,6); б) (–40; 0), (0; –28); в) (–5; 0), (0; 6); г) (0,4; 0), (0; 2). 3. № 325. При выполнении этого задания учащиеся замечают, что для построения графика линейной функции частного вида y = b достаточно построить точку с координатами (0; b) и провести прямую, параллельную оси х (если выполняем задание в тетради в клеточку), либо построить 2 точки с координатами (0; b) и (х0; b), где х0 – любое число, и провести через них прямую. |