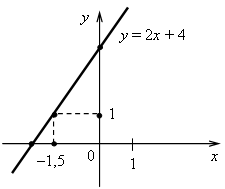планы7а. Урок 1 Числовые выражения
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
IV. Объяснение нового материала. 1. Напоминаем, что график прямой пропорциональности y = kx располагается в I и III или в II и IV координатных четвертях в зависимости от знака коэффициента k. Посмотрев в тетради выполненные ранее построения, замечаем, что графики линейных функций пересекают ось х либо под острым углом (с положительным направлением оси х), либо под тупым. Угол зависит от знака k. Если k = 0, то прямая параллельна оси х. Так как от k зависит угол, то k называют угловым коэффициентом прямой. 2. Затем рассматриваем и анализируем рис. 36, 37 со с. 73 учебника. Делаем вывод: если угловые коэффициенты прямых, являющихся графиками двух линейных функций, равны, то эти прямые параллельны, а если угловые коэффициенты различны, то прямые пересекаются. 3. Рассматриваем случай, когда у линейных функций k различны, а b – одинаковые. Во время актуализации знаний мы вспомнили, что графики этих функций все проходят через точку (0; b), значит, они все пересекаются в этой точке. V. Формирование умений и навыков. 1. Постройте в одной системе координат графики функций: у = Ответьте на вопросы: 1) Чему равен угловой коэффициент каждой прямой? 2) Каково взаимное расположение графиков функций? 3) Каковы координаты точек пересечения каждого графика с осями координат? 2. Пересекаются ли графики функций у = 2х – 4 и у = –4х + 2; у = 2х – 3 и у = 2х + 3? В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением. 3. № 327. 4. Постройте прямую, если её угловой коэффициент равен –0,5 и она проходит через точку (–6; 4). Задайте формулой линейную функцию, график которой параллелен этой прямой и пересекает ось у в точке (0; 5). VI. Итоги урока. – Дайте определение линейной функции. – Что является графиком линейной функции? Как его построить? – Почему коэффициент k называется угловым? Как от k зависит расположение графика линейной функции? – В каком случае графики двух линейных функций пересекаются и в каком случае они являются параллельными прямыми? Домашнее задание: № 323; № 326; № 328; № 329. Урок 36 Взаимное расположение графиков линейных функций Цели: формировать умение использовать знания о линейной функции и её график при решении практических задач; интерпретировать полученные результаты. Ход урока I. Устная работа. Тест. 1. Отметьте знаком «+» пары функций, графики которых пересекаются: а) у = в) у = 3х + 1 и у = х + 1; г) у = 2х + 5 и у = 2х – 10. 2. Даны функции: а) у = 0,75х;б) у = выпишите функции, графики которых параллельны графику функции у = 0,75х – 5. 3. Найдите координаты точки пересечения графиков функций у = 37х – 8 и у = 25х + 4. III. Формирование умений и навыков. 1. № 330, 332. 2. Дорожный просвет – это расстояние между днищем автомобиля и дорогой, на которой он стоит. Для некоторого легкового автомобиля дорожный просвет можно вычислить по формуле h = 40 – а) Вычислите дорожный просвет, если масса груза в автомобиле равна: 100 кг; 150 кг; 200 кг; 0 кг. б) Является ли зависимость величины дорожного просвета от массы груза, погруженного в автомобиль, линейной функцией? Чему в этом случае равны коэффициенты k и b? в) Начертите координатные оси, выбрав на них подходящий масштаб, и постройте график функции h = 40 – г) С помощью построенного графика найдите, какой груз погружен в автомобиль, если дорожный просвет равен: 33 см; 38 см; 35 см; 40 см. д) С помощью графика определите: 1) на сколько сантиметров уменьшится дорожный просвет, если к грузу в 50 кг добавить груз в 25 кг; к грузу в 100 кг добавить груз в 25 кг; 2) на сколько сантиметров увеличится дорожный просвет, если с машины с грузом в 150 кг снять груз в 50 кг. 3. № 1201*. Решение: а) y = | x | – 3. Данную функцию можно переписать в виде:
б) y = 4 – | x |.
IV. Итоги урока. – Какая функция является линейной? – Что является графиком линейной функции? – Как называется коэффициент k? Что он показывает в формуле линейной функции? – Как расположен график функции y = x + 2; у = –3х; y = – Назовите признак параллельности графиков двух линейных функций. Домашнее задание: № 332; 333; 335; 366. Урок 37 Взаимное расположение графиков линейных функций Цели: обобщить и систематизировать знания по теме «Линейная функция»; подготовиться к написанию контрольной работы. Ход урока I. Игра-слалом. Класс разбивается на 3 команды. Игра состоит из теоретического и практического конкурсов. Задания выполняются на время. Побеждает команда, получившая наибольшее число правильных ответов за наименьшее время. 1. Теоретический конкурс 1. Какую зависимость называют функциональной или функцией? 2. Что такое аргумент и что такое функция? 3. Что называют областью определения функции? 4. Что такое график функции? 5. Какую функцию называют линейной? 6. Что является графиком линейной функции? 7. Что является графиком прямой пропорциональности? 8. В чём их сходство и различие? 9. От чего зависит расположение графика линейной функции? 10. Сколько точек необходимо для построения графика линейной функции? 11. А для графика прямой пропорциональности? Почему? 12. Что такое угловой коэффициент? 13. Как расположен график функции y = kx при k > 0 и k < 0? 14. Как найти координаты точки пересечения графиков двух линейных функций? 15. В каком случае графики двух линейных функций являются параллельными прямыми? 2. Практический конкурс 1. Заполните таблицу для функции, заданной формулой у = –0,5(8 – x).
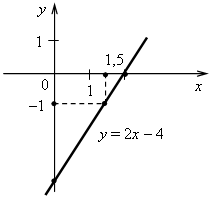
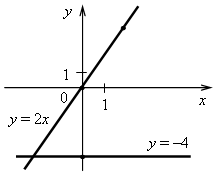
2. Какова область определения функции? а) у = б) у = 7х + 6; г) у = 3. Является ли линейной функция: а) у = б) у = 3(х + 8); г) у = 2(1 – 3х)(х – 3)? 4. Постройте график функции, заданной формулой у = 2х + 3. 5. Постройте график функции, заданной формулой у = 0,5х + 3. С помощью графика найдите: а) значение у, если х = –4; б) значение х, если у = 6; в) координаты точек пересечения графика с осями координат; г) корень уравнения 0,5х + 3 = 0. 6. Не выполняя построения, выясните, проходит ли график функции, заданной формулой у = 1,25х – 5, через точку: а) А (20; 20); б) В (20; 10). 7. Функция задана формулой у = 0,25х + 3, где х принадлежит промежутку от –4 до 8. Постройте график этой функции и укажите все целые значения, которые может принимать эта функция. 8. Пересекает ли ось х график линейной функции, и если пересекает, то в какой точке? Функция задана формулой: а) у = 7х + 49; б) у = 15. 9. График некоторой линейной функции вида y = kx + 1 параллелен графику функции у = –0,4х. Найдите значение коэффициента k и выясните, принадлежит ли этому графику точка М (50; –19). 10. Не выполняя построения, найдите координаты точки пересечения графиков линейных функций: у = 4х + 9 и у = 6х – 5. 11. Отметьте точки А (–4; 3) и В (2; –6). Проведите прямую АВ и найдите координаты точек пересечения этой прямой с осью х и осью у. 12. Постройте график функций: а) у = –5; б) х = 3. 13. Какие из графиков функций параллельны, а какие пересекаются: а) у = –3х + 4; в) у = –(2 + 3х); б) у = –х + 3; г) у = х + 3? 14. В одной и той же координатной плоскости постройте графики функции: у = 5, у = х – 2, у = –2х + 4, у = 0. 15. В каких координатных четвертях расположен график прямой пропорциональности, параллельный графику линейной функции, заданной формулой: а) у = 0,8х – 1,6; б) у = – 0,4х + 1? II. Итоги урока. Домашнее задание: повторить п. 15, п. 16. № 360; № 363; № 372. Урок 40 Контрольная работа № 3 Вариант 1 1. Функция задана формулой у = 6х + 19. Определите: а) значение у, если х = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точку А (–2; 7). 2. а) Постройте график функции у = 2х – 4. б) Укажите с помощью графика, чему равно значение у при х = 1,5. 3. В одной и той же системе координат постройте графики функций: а) у = –2х; б) у = 3. 4. Найдите координаты точки пересечения графиков функций у = 47х – 37 и у = –13х + 23. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат. Вариант 2 1. Функция задана формулой у = 4х – 30. Определите: а) значение у, если х = –2,5; б) значение х, при котором у = –6; в) проходит ли график функции через точку В (7; –3). 2. а) Постройте график функции у = –3х + 3. б) Укажите с помощью графика, при каком значении х значение у равно 6. 3. В одной и той же системе координат постройте графики функций: а) у = 0,5х; б) у = –4. 4. Найдите координаты точки пересечения графиков функций у = –38х + 15 и у = –21х – 36. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат. Вариант 3 1. Функция задана формулой у = 5х + 18. Определите: а) значение у, если х = 0,4; б) значение х, при котором у = 3; в) проходит ли график функции через точку С (–6; –12). 2. а) Постройте график функции у = 2х + 4. б) Укажите с помощью графика, чему равно значение у при х = –1,5. 3. В одной и той же системе координат постройте графики функций: а) у = –0,5х; б) у = 5. 4. Найдите координаты точки пересечения графиков функций у = –14х + 32 и у = 26х – 8. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат. Вариант 4 1. Функция задана формулой у = 2х – 15. Определите: а) значение у, если х = –3,5; б) значение х, при котором у = –5; в) проходит ли график функции через точку K (10; –5). 2. а) Постройте график функции у = –3х – 3. б) Укажите с помощью графика, при каком значении х значение у равно –6. 3. В одной и той же системе координат постройте график функций: а) у = 2х; б) у = –4. 4. Найдите координаты точки пересечения графиков функций у = –10х – 9 и у = –24х + 19. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат. Рекомендации по оцениванию. Задания 1–3 относятся к базовому уровню знаний по теме. Верное выполнение любых трех заданий оценивается отметкой «3». Для получения отметки «5» необходимо выполнить верно все пять заданий. Решение заданий контрольной работы Вариант 1 1. у = 6х + 19. а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22; б) если у = 1, то 6х + 19 = 1; 6х = 1 – 19; 6х = –18; х = –18 : 6; х = –3; в) 7 = 6 · (–2) + 19; 7 = –12 + 19; 7 = 7 – верно, значит, график функции проходит через точку А (–2; 7). Ответ: а) 22; б) –3; в) проходит.
60х = 60; х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты: если х = 1, то у = 47 · 1 – 37 = 10. Точка пересечения имеет координаты (1; 10). Ответ: (1; 10). 5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х. Ответ: у = 3х. Вариант 2 1. у = 4х – 30. а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40; б) если у = –6, то 4х – 30 = –6; 4х = –6 + 30; 4х = 24; х = 24 : 4; х = 6; в) –3 = 4 · 7 – 30; –3 = 28 – 30; –3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3). Ответ: а) –40; б) 6; в) не проходит.
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2). б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.  4. Решим уравнение: –38х + 15 = –21х – 36; –38х + 21х = –36 – 15; –17х = –51; х = (–51) : (–17); х = 3, значит, абсцисса точки пересечения графиков функций равна 3. Найдем соответствующее значение ординаты: если х = 3, то у = –38 · 3 + 15 = –99. Точка пересечения имеет координаты (3; –99). Ответ: (3; –99). 5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х. Ответ: у = –5х. Вариант 3 1. у = 5х + 18. а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20; б) если у = 3, то 5х + 18 = 3; 5х = 3 – 18; 5х = –15; х = –15 : 5; х = –3; в) –12 = 5 · (–6) + 18; –12 = –30 + 18; –12 = –12 – верно, значит, график функции проходит через точку С (–6; –12). Ответ: а) 20; б) –3; в) проходит.
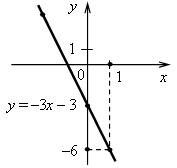
3. а) у = –0,5х. Графиком является прямая, проходящая через начало координат и точку (4; –2). б) у = 5. Графиком является прямая, проходящая через точку (0; 5) и параллельная оси х. 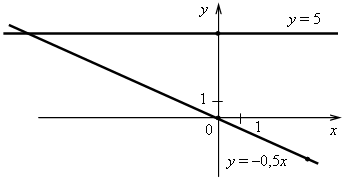 4. Решим уравнение: –14х + 32 = 26х – 8; –14х – 26х = –8 – 32; –40х = –40; х = 1, значит, абсцисса точки пересечения графиков равна 1. Найдем соответствующее значение ординаты: если х = 1, то у = –14 · 1 + 32 = 18. Точка пересечения имеет координаты (1; 18). Ответ: (1; 18). 5. График параллелен прямой у = 2х + 9, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 2х. Ответ: у = 2х. Вариант 4 1. у = 2х – 15. а) Если х = –3,5, то у = 2 · (–3,5) – 15 = –7 – 15 = –22; б) если у = –5, то 2х – 15 = –5; 2х = –5 + 15; 2х = 10; х = 5; в) –5 = 2 · 10 – 15; –5 = 20 – 15; –5 = 5 – неверно, значит, график функции не проходит через точку K (10; –5). Ответ: а) –22; б) 5; в) не проходит.
4. Решим уравнение: –10х – 9 = –24х + 19; –10х + 24х = 19 + 9; 14х = 28; х = 28 : 14; х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты: если х = 2, то у = –10 · 2 – 9 = –29. Точка пересечения имеет координаты (2; –29). Ответ: (2; –29). 5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х. Ответ: у = –8х. Урок №39 Определение степени с натуральным показателем Цели: ввести понятие степени числа а с натуральным показателем п; определить значение степени с натуральным показателем положительного и отрицательного числа в зависимости от четности / нечетности показателя степени; формировать умение вычислять значение степени и представлять число в виде степени с натуральным показателем. |