разработка урока. Урок 47 Тема. Сумма и разность кубов
 Скачать 25.38 Kb.
|
|
Урок № 47 Тема. Сумма и разность кубов Цель: добиться сознательного усвоения содержания формул (a ± b)(a2  ab + b2) = a3 ± b3 и выработать базовые умения применять эти формулы для соответствующих преобразований целых выражений в многочлен стандартного вида. Тип урока: усвоение знаний. Ход урока I. Организационный момент @ Учитель проверяет готовность учащихся к уроку, настраивает их на работу. II. Проверка домашнего задания @ Чтобы проверить качество выполнения домашнего задания, собираем тетради. Поскольку выполнение упражнений № 1-2 домашнего задания предусматривало использование как базовых, так и умений более высокого уровня, удачно выполненное домашнее задание можно отнести как домашнюю самостоятельную работу (с выставлением оценок в журнал). III. Формулировка цели и задач урока @ Учитель напоминает ученикам (или побуждает их к самостоятельной работе по осознанию места раздела, что изучается: «Формулы сокращенного умножения» по теме «Многочлены и действия с ними») и формулирует цель урока: продолжить работу по изучению формул сокращенного умножения; выработать умение применять новые знания для преобразования целых выражений в многочлен стандартного вида. IV. Актуализация опорных знаний Выполнение устных упражнений 1. Прочитайте выражение: 1) (а - b); 2) (а + b); 3) (а - b)2; 4) (а + b)2; 5) а2 - 2аb + b2; 6) а2 + 2аb + b2; 7) а3 - b3; 8) а3 + b3; 9) а2 - аb + b2; 10) а2 + аb + b2. 2. Представьте в виде многочлена: (a + b)2; (a - b)2; (а + b)(а - b); (а + b)(с + d). V. Изучение нового материала 1. Работа с опережающим домашним заданием. Задача 1. Используя правило умножения многочлена на многочлен, выполните умножение многочленов. Образованные выражения (многочлены) сведите к стандартному виду: 1) (а - b)(а2 + аb + b2); 2) (а + b)(а2 - аb + b2); 3) (с - d)(с2 + сd + d2); 4) (с + d)(с2 - сd + d2); 5) (m - 1)(m2 + m + 1); 6) (m + 1)(m2 - m + 1). Задание 2. Выпишите условие каждого из заданий и многочлен стандартного вида, тождественно ему равен, и запишите соответствующие равенства. Прочитайте эти равенства, используя термины «сумма», «произведение», «разница», «квадрат». Сравните получившиеся равенства и сделайте вывод. 2. Усвоение знаний. @ После проделанной работы (см. п. 1) традиционно учитель вместе с учениками формулирует сначала в виде тождества, а затем с помощью слов формулы, которые имеют название «сумма и разность кубов двух выражений). В конспектах учащиеся могут сделать соответствующие записи.
При этом следует обратить внимание, что выделенные слова помогают лучше запомнить содержание формул (потому что часто ученики, не задумываясь над содержанием, допускают в этих местах ошибок). VI. Усвоение умений Выполнение устных упражнений 1. Назовите неполный квадрат разности выражений: 1) x i y; 2) c i d; 3) г i 1; 4) 2 i c. 2. Назовите неполный квадрат суммы выражений: 1) m и n; 2) р и q; 3) а и 1; 4) 3 и х. Выполнение письменных упражнений 1. Упростите выражения: 1) (а - b)(а2 + аb + b2); 2) (с + d)(с2 - сd + d2); 3) (m - n)(m2 + mn + n2); 4) (х + у)(х2 - ху + у2). 2. Преобразуйте в многочлен стандартного вида: 1) (х2 - 1)(х4 + х2 + 1) + 1; 2)(а2 + b 2)(а2 - а2b2 + b4) - а6 - b6; 3) (а + 2)(а2 - 2а + 4) - (а - 2)(а2 + 2а + 4); 4) (х + 2)(х2 - 2х + 4) - х(х - 3)(х + 3); 5) (7а2 - 1)(49а4 + 7а2 + 1) - 4а2(5а2 - 1)2 + (5а2 - 3)(3 - 8а2); 6*) (a + 1)(а - 1)(а2 - а + 1)(а2 + а + 1)(а6 + 1)(а12 + 1)(а24 + 1). * Во время выполнения этого задания желательно добиться от учащихся понимания того, что действия каждого ученика при преобразовании целых выражений должны быть не спонтанными, а сознательными, то есть подчиняться определенной последовательности: 1) Устанавливаем порядок выполнения действий, определенный условием задачи. 2) Ищем в выражении произведения, которые можно преобразовать в многочлен по формулам (не забываем о возможности применения законов умножения и свойств степени). 3) Если произведения многочленов не соответствуют ни одной из формул, используем алгоритм умножения многочленов. 4) После выполнения умножения используем другие действия с многочленами (сложение, вычитание, возведение подобных слагаемых). 3. Решите уравнение: 1) (х - 2)(х2 + 2х + 4) = х3 + 4х; 2) (у2 - 3у + 9)(у + 3) = 6у + у3; 3) (4 - 5х)(16 + 20х) + 25х2 + 5х(5х - 2)(5х + 2) = 4; 4) 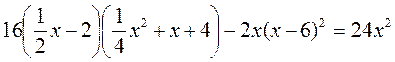 .4* (дополнительно). Логические упражнения (на повторение). Какое число или выражение пропущены?
VII. Итоги урока Заполните пропуски, чтобы записи стали верными: 1) ...суммы двух выражений на неполный квадрат их... равно... кубов двух выражений; 2) (... - 1)(a2 ... a ... 1) = a3 - ... VIII. Домашнее задание № 1. Упростите выражение: 1) (х - 2)(х2 + 2x + 4) - (1 - х)(х2 + x + l); 2) (х - 3)(х2 + 3х + 9) - (х + 1)(х - 1)(х - 2); 3) а(а - 3)(а + 3) - (а + 2)(а2 - 2а + 4); 4) (3а2 + 1)(9а4 - 3а2 + 1) - 3а2(2а2 + 1)2 + (5а2 - 1)(2 - 3а2). № 2. Решите уравнение: 1) (2 - 3х)(4 + 6х + 9х2) + 3х(3х - 1)(3х + 1) = х; 2) 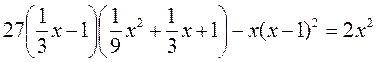 .№ 3. Опережающее домашнее задание. 1) Пользуясь соответствующим пунктом учебника и записями в тетради, повторите содержание понятий и алгоритмов: · разложение на множители; · вынесение общего множителя за скобки; · разложение многочленов на множители способом группировки. 2) Выпишите в столбик все изученные формулы сокращенного умножения. Являются ли данные равенства тождественностями? Запишите эти тождества, поменяв местами левую и правую часть каждого равенства. |