база данных. Урок 7 Тема Пропорции Мы знаем с прошлых уроков, что отношение
 Скачать 124.33 Kb. Скачать 124.33 Kb.
|
|
Математика 10.10.2022 6А, 6Б Урок №7 Тема: Пропорции Мы знаем с прошлых уроков, что отношение – это частное (деление) двух неравных нулю чисел (или величин). Рассмотрим два отношения:  Нетрудно посчитать, чему же равны значения этих частных:  Видно, что и в первом и во втором случае значения частных равны. А значит и сами отношения равны. Такое равенство в математике называют пропорцией. Отношение можно записывать с помощью знака деления и при помощи черты дроби. Следовательно, пропорцию можно записать ещё в виде равенства обыкновенных дробей: Пропорция — это равенство двух отношений. Пропорцию можно записать в буквенном виде: в строчку и в виде равенства двух дробей:  a, b, c и d – называют членами пропорции. a, b, c и d – называют членами пропорции.Числа a и d называются крайними членами пропорции, Числа b и с – средними членами пропорции: Пропорцию a : b = c : d или  = =  читают так: читают так: - «отношение a к b равно отношению c к d» или - «a относится к b как с относится к d» 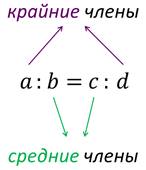 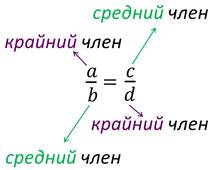 Пример 1. Вычислите произведение крайних членов пропорции, затем произведение средних членов пропорции и сравните полученные результаты: а) 12 : 6 = 30 : 15. Произведение крайних членов: 12 15 = 180. Произведение средних членов: 6 30 = 180. Т.е. 180 = 180; б) 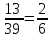 , ,13 6 = 78, 39 2 = 78, т.е. 78 = 78. На основании полученных результатов, какой вывод мы можем сделать? Если пропорция составлена верно, то выполняется следующее. Основное свойство пропорции Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов a · d = b · c, то пропорция a : b = c : d верна. Оно называется признаком пропорции. Но ведь пропорцию записывают и в виде:  Они лежат «крест-накрест»! Чтобы правильно применять правило, давайте запомним правило (креста) «X». Пример №2. Правильно ли составлена пропорция?  1 способ (по определению пропорции. Находим значение левой и правой части и сравниваем их)  = 9; = 9; 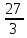 = 9, = 9, 9= 9 Ответ: верная пропорция. 2 способ (по основному свойству пропорции. Чтобы проверить верно ли составлена попорция, перемножим ее крайние члены. Далее перемножим средние члены. Сравниваем полученные значения) Запишем пропорцию и нарисуем карандашом поверх знака равенства крест.  Делаем вывод, что пропорция составлена верно. Делаем вывод, что пропорция составлена верно.Ответ: верная пропорция. Нарисовав крест, гораздо легче составить нужное произведение (проверить выполнение основного свойства пропорции). Решение упражнений. Учебник, с.16 № 46(а). Запишите в виде пропорции: а) 2 относится к 3, как 10 относится к 15,  . .Учебник с.16 № 47(а,в). Можно ли составить пропорцию из отношений: а) 6 : 3 и 24 : 12, 6 : 3 = 2, 24 : 12 = 2, 2 = 2, значит составить пропорцию можно; в) 2 : 5 и 10 : 4, 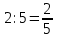 , , 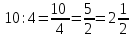 , ,  , значит составить пропорцию нельзя. , значит составить пропорцию нельзя.Учебник, с.16 № 49(а,в). Верно ли равенство: (по определению пропорции) а)  , (используем определение пропорции – найдем отношение левой части, затем найдем отношение правой части и сравним полученные значения) , (используем определение пропорции – найдем отношение левой части, затем найдем отношение правой части и сравним полученные значения)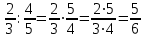 ; ; ; ; , то равенство верно по определению пропорции; , то равенство верно по определению пропорции;в) 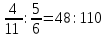 , (используем определение пропорции) , (используем определение пропорции) ; ;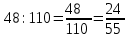 ; ;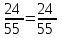 , то равенство верно по определению пропорции. , то равенство верно по определению пропорции.Учебник, с.16 № 50(а,в). Верно ли равенство: (по основному свойству пропорции) а) 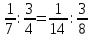 , (используем свойство пропорции) , (используем свойство пропорции)Перемножаем крайние члены пропорции: 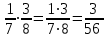 ; ;Перемножаем средние члены пропорции: 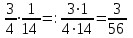 ; ;Произведение крайних членов пропорции равно 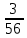 , произведение средних членов пропорции также равно , произведение средних членов пропорции также равно 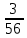 . .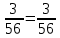 Делаем вывод, что пропорция 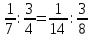 составлена верно. составлена верно.в) 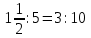 , (используем свойство пропорции) , (используем свойство пропорции) ; ;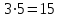 ; ; , то равенство верно по свойству пропорции. , то равенство верно по свойству пропорции.Учебник, с.17 № 51(а). Замените пропорцией равенство: а) 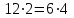 , , . .Изучить тему Вам поможет видеоурок: https://resh.edu.ru/subject/lesson/6841/main/315185/ ДОМАШНЕЕ ЗАДАНИЕ Изучить п.1.4 (стр 14). Решить: № 49. |
