статья. Урок математики и физики преподаватель физики Мынзат В. Н

• Название: Урок математики и физики преподаватель физики Мынзат В. Н
• Дата: 01.11.2022
• Размер: 56.66 Kb.
• Имя файла: статья .docx
• Тип: Урок; #765704

НЕТРАДИЦИОННЫЕ ФОРМЫ ПРОВЕДЕНИЯ УРОКА.

ИНТЕРИРОВАННЫЙ УРОК МАТЕМАТИКИ И ФИЗИКИ
преподаватель физики Мынзат В.Н.

г. Омск
         Для того, чтобы увлечь и заинтересовать учащихся математикой и физикой, необходимо творчески подходить к подготовке к занятию, к изложению темы урока.

Решение большинства физических задач требует от учащихся математических знаний. Решение широкого круга физических задач сводится к составлению уравнения у = f(х) с входящими в него тригонометрическими функциями.

         Например, изложение вопроса «Колебательное движение» с точки зрения физики и математики даст возможность сделать преподавание этой темы более интересным, будет побуждать учащихся к активной деятельности в процессе обучения, будет способствовать углублению некоторых понятий физики, а самое главное, подчеркивает связь математики с другими дисциплинами естественно – математического цикла.

Именно эта тема более актуальна для такого типа урока, так как колебательное движение одно из самых распространенных движений в природе и технике. Колебания играет огромную роль в жизни человека. Без знаний законов колебаний нельзя было бы создать радио телевидение и многие другие современные устройства.

Колебания многогранны. Поэтому необходимо всестороннее их изучение с помощью законов физики и математических понятий.

Рассматриваемые задачи были подобраны с учетом рациональной последовательности их предъявления: от репродуктивных, направленных на актуализацию знаний, к частично – поисковым, ориентированным на овладение обобщенными приемами познавательной деятельности.

Урок проводится в кабинете физике с использованием компьютера.

Тема урока: Колебания

Цели урока: 1.Развитие представлений о колебательных процессах с применением производной.

2.Активизация мыслительной творческой деятельности, создание проблемной ситуации.

3.Привитие интереса к изучению физики и математики.

Оборудование: Компьютер, осциллограф, звуковой генератор, колебательный контур.

На протяжении всего урока по каждому вопросу демонстрировались слайды презентации с помощью мультимедийного проектора.

Ход урока:

Учитель физики.

1. Вводная беседа о значимости колебательных явлений в жизни человека, их распространенности и многообразии в природе и технике.

    Без математики не возможно вывести ни один физический закон. Математика является инструментом для физики. Посмотрим, как изучая тему «Колебания» математика помогает разобраться в этих процессах.

2. Фронтальный опрос:

а) что такое колебания;

б) какие колебания называются свободными;

в) какие колебания называются вынужденными;

г) какими величинами характеризуются колебательные процессы;

д) как получить свободные электромагнитные колебания;

ж) какие системы называют автоколебательными;

з) какое уравнение описывает колебательные процессы в контуре.

q˝

 Если 1/LC обозначить через  то получим уравнение: q˝ = - q

          Учитель математики: А так как заряд изменяется с течением времени, то это есть функция от времени и в математике её можно записать в виде: f˝   

Мы видим что в уравнении встречается запись f˝(t) Это есть вторая производная.

          Производная от производной f΄функции называется второй производной функции f и обозначается f˝(t). А что такое производная с точки зрения физики (Скорость изменения величины). Значит, вторая производная, есть скорость изменения этой скорости.

Рассмотрим пример:

Возьмем функцию y = sin x Найдем первую производную sin΄ x = cos x

Найдем вторую производную sin˝ x = cos΄ x = - sin x.

          Мы видим, что для данной функции вторая производная отличается от самой функции только знаком. Величины, которые изменяются во времени по закону sin и cos совершают гармонические колебания.

А уравнение f˝(t) = - f(t) называется дифференциальным уравнением гармонических колебаний.

Уравнение f(t) = Acos ( t + ) есть решение дифференциального уравнения гармонических колебаний.

f˝ (t) = - f(t). Проверим это: f΄(t) = -A  sin( t +  ) f˝(t) = - A cos ( t +  ) = - f(t)

          Учитель физики: В колебательном контуре мы знаем заряд изменяется с течением времени по закону g = g_m cos (t)  (1)

Если заряд изменяется с течением времени то в цепи есть переменный электрический ток. При гармонических колебаниях заряд, сила тока и напряжение тоже совершают гармонические колебания.

Если мы знаем закон, по которому изменяется заряд, то как получить закон, по которому изменяется сила  тока?

i = g΄ = -g_m sin t   (2)

Увидеть гармонические колебания силы тока можно с помощью осциллографа.

          Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока.

Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять собой синусоиду.

Обратим внимание на уравнение 1 и 2. Чем они отличаются? А какая физическая величина даёт возможность отличить одно гармоническое колебание от другого? Что такое фаза колебаний?  Как найти разность фаз?

Для того чтобы найти разность фаз, надо чтобы обе величины изменялись по одному и тому же закону

Учитель математики: Как из одной функции получить другую. (С помощью формул приведения.) i = g΄ = -g_m  sin t = I_mcos ( t +  ) где I_m = g_m 

(Пояснить подробно применение формул приведения).

 Учитель физики: Колебания чего, силы тока или заряда опережают и насколько? Не только колебания заряда и силы тока не совпадают по фазе. Если в цепи переменного тока есть конденсатор или катушка, то колебания силы тока и напряжения не совпадают по фазе. Посмотрим на рисунки.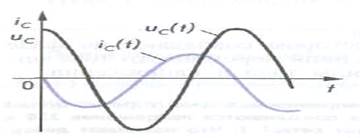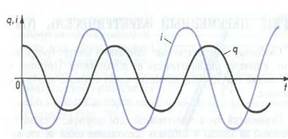



ЗАДАЧА № 953 (Р)

Дано:                                 Решение:

Ф = 0,01 sin 10 t           Ф = Ф_м sin t                     е = Ф΄

t = 0                                 Ф_м = 0,01Вб                       е = -(0,01 sin 10  t)΄ =

                                          = 2                               =-0,01•10 cos 10 t          

е = е(t)                               =                                  = - 0,1  sin ( 10  t +  )                                       

 - ?                                   =   = 5 Гц.                   Е_м = - 0,314В

Ф_м =?

Е_м -?   -?                                 Ответ:  5 Гц;  0,01Вб;  - 0,314В.

Учитель математики. Если есть два гармонических колебания, то они могут накладываться. Что получается в результате наложения? Это задача математическая. Пусть два гармонических колебания заданны функциями

y₁ = cos 2x  и y₂ = -sin x. Рассмотрим по рисунку решение этой задачи.

Для того что бы решить эту задачу  надо построить графики этих функций.

Так как функции y1 и y₂ периодические с основными периодами соответственно T₁ =   и T₂ = 2 , то и функция y = cos2x – sinx периодическая с периодом T = 2 . Поэтому график функции рассмотрим на промежутке [- ; ]. Сложить ординаты ряда характерных точек (где одно из слагаемых равно 0, где y₁ = y₂; y₁ = - y₂) найдем ряд точек искомого графика. Соединив эти точки плавной кривой, получим, что искомый график имеет вид: (на рисунке изображен сплошной линией.) Вне промежутка график получается, по свойству периодичности функций.

Полученная кривая – график сложного гармонического колебания.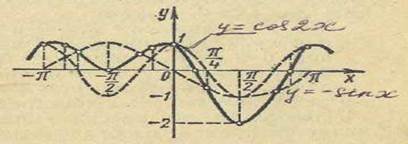



Можно доказать аналитически, что сумма двух гармонических колебаний есть функция периодическая.

 Учитель физики. Мы рассмотрели многие вопросы, связанные с колебаниями с точки зрения физики и математики. Посмотрим фильм, где есть эксперименты по колебаниям.

ФИЛЬМ.

Учитель математики. Резерв № 568, № 573.

ИТОГ УРОКА: Учитель физики. Посмотрели на колебательные процессы с точки зрения физики и математики. Это сложные процессы, но в жизни они довольно распространенны, без этих процессов невозможно смотреть телевизор, слушать радио и т.д.

Данный урок построен на деятельной основе с использованием компьютерной и развивающей технологий.
                     Список используемой литературы:

     Учебник: 1. Физика 10   Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. / М.:   Просвещение, 2015.

1.     Тихомирова С.А. Дидактические материалы по физике: 7-11 кл.- М.: Школьная Пресса, 2003.

2.     Перельман Я.И. Занимательная физика. Кн. 1.- М.: Наука, 1986.

3.     Усова А.В. Краткий курс истории физики: Учебное пособие.- Челябинск: Факел ЧГПИ, 1995.

4.      Физика. Задачник. 10-11 кл.: Пособие для общеобразоват. учреждений / Рымкевич А.П. – 7-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.

5.       Сауров Ю.А. Физика в 11 классе: Модели уроков: Кн. Для учителя. – М.: Просвещение, 2014

6.       В.Г. Маркина. Физика 11 класс: поурочные планы по учебнику Г.Я. Мякишева, Б.Б. Буховцева. – Волгоград: Учитель, 2006

7.  С.Н. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. Алгебра и начала анализа.                   Учебник 11класс. Москва «Просвещение» 2015 г.

2.  М.К. Потапов, А.В. Шевкин. Алгебра и начала анализа.

Дидактические материалы для 11 класса.- Москва «Просвещение» 2016г.

3.   Ю.В, Шепелев. Алгебра и начала анализа. Тематические и итоговые тесты для 11 класса. -Москва «Просвещение» 2015г.

4.   М.К. Потапов, А.В. Шевкин. Алгебра и начала анализа. Книга для учителя 11 класса. -Москва «Просвещение» 2016г.