Урок по теме Параллельность прямых и плоскостей. Бушева Инга Николаевна учитель математики
 Скачать 2.84 Mb. Скачать 2.84 Mb.
|
|
Обобщающий урок по теме «Параллельность прямых и плоскостей». Бушева Инга Николаевна учитель математики Урок проводится в форме урока-погружения (не менее 90 минут), что позволяет повторить учебный материал, осуществить контроль знаний учащихся и их коррекцию. На уроке уделяется внимание следующим разделам : 1. Аксиомы стереометрии 2. Взаимное расположение прямых в пространстве. 3. Взаимное расположение в пространстве прямой и плоскости. 4. Взаимное расположение в пространстве двух плоскостей. Таким образом, урок разделен на 4 блока. Во время работы над каждым из блоков учащиеся проходят через следующие этапы: 1. повторение теории 2. тесты (теория) 3. решение задач Ребята выполняют задания, составленные учителем с учетом индивидуальных возможностей учащихся. Урок дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условие для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся; обеспечивает непрерывное образование и устраняет перегрузку домашнего задания. У учащихся есть возможность: - работать самостоятельно с дифференцированной программой; - вернуться к учебному материалу, если в этом есть необходимость; - получить консультацию и дозированную персональную помощь от учителя или соседа по парте. На уроке создается комфортная обстановка - индивидуальный темп (для сильных учащихся предлагаются дополнительные задачи), - «мягкий» контроль (проверка работы товарищем, с помощью демонстрационного образца). Для самостоятельной оценки деятельности учащимся предлагаются критерии, с помощью которых ученики подсчитывают свои баллы, и после 4 блока, выставляют себе оценку самостоятельно. Во время самостоятельной работы учитель проверяет объективность выставленных оценок. Преподаватель на уроке управляет процессом обучения, консультирует ребят , помогает и поддерживает учеников. Цели урока: 1. Общеобразовательные: организовать работу учащихся по систематизации знаний основных теоретических вопросов темы; закрепить и углубить знания и умения учащихся применять аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых, прямой и плоскости, параллельности плоскостей. 2. Развивающие: создать условия для развития познавательной активности учащихся, познавательного интереса к предмету; развивать навыки самостоятельной деятельности учащихся; развивать навыки самоконтроля; развивать активности учащихся, формировать учебно-познавательных действий, коммуникативных, исследовательских навыков учащихся, умение анализировать и устанавливать связь между элементами темы. 3. Воспитательные: создать условия успешности ученика на уроке; воспитывать культуру умственного труда; способность к самоанализу, рефлексии; развивать умение рецензировать и корректировать ответы товарищей. воспитывать умение критически относиться к результатам деятельности; обеспечить гуманистический характер обучения; Оборудование: компьютер, мультимедийный проектор, раздаточный материал, демонстрационные образцы. План урока 1. Организационная часть – постановка целей и задач урока – 1 минута. 2. Мотивационная – разъяснение необходимости решения задач данного цикла в реальной ситуации – 1 минута. 3. Погружение. - Актуализация опорных знаний (повторение теории, доказательство теорем) – 5+5+5+15=30 мин. - Закрепление полученных знаний (тесты, задачи). 10+10+9+11 =40 минут. по блокам 4. Контроль полученных знаний. Выполнение самостоятельной работы – 15 минут. 5. Рефлексия. Подведение итогов – 2 минуты. 6. Домашнее задание – 1 минута. Ход урока. 1. Организационный момент. Сегодня мы с вами должны подняться ещё на одну ступеньку вверх, «преодолевая» задачи, которые будут рассматриваться на уроке. Сегодня мы начинаем повторение темы «Параллельность прямых и плоскостей в пространстве». Наша задача вспомнить все, что мы знаем по этой теме. Учащиеся самостоятельно формулируют задачи урока. 2. Мотивационный момент Мы должны закрепить и углубить наши знания по этой теме. Эти знания пригодятся нам для решения практических задач, для успешной сдачи ЕГЭ. Вы должны научиться анализировать и устанавливать связь между элементами темы. Развить свою активность, сформировать учебно - познавательные действия, коммуникативные навыки. Хотелось бы создать условия вашей успешности на уроке; чтобы вы проявили способность к самоанализу, рефлексии, умение рецензировать и корректировать ответы товарищей. А каковы пути и средства достижения этих целей? Домашнее задание к сегодняшнему уроку заключалось в том, чтобы вы повторили пункты 1- 12, просмотрели и еще раз разобрали задачи, которые мы решали в этих пунктах для обобщения и закрепления темы «Параллельность прямых и плоскостей в пространстве». У вас на столах лежат: памятки для работы на уроке - листы самоконтроля, в них вы сами оцениваете свои знания и работу на каждом этапе урока. Эти листы помогут организовать повторение на последующих уроках. Блок 1. Аксиомы стереометрии Цели блока: - повторить аксиомы стереометрии и применение их при решении задач домашнего задания; следствия из аксиом; - закрепить умение применять аксиомы стереометрии и следствия из аксиом при решении задач;. Актуализация опорных знаний. Проведем теоретическую разминку. Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. 1. Сформулируйте три аксиомы о взаимном расположении точек, прямых и плоскостей. 1. Аксиомы стереометрии (Учащиеся составляют таблицы).
• В ходе беседы выделяются существенные моменты теории: а) разъяснить содержание аксиом и иллюстрировать на модели; б) чтение учащимися текста аксиом; в) выполнение чертежа; г) запись содержания с помощью символов. 2. Как формулируются следствия из этих аксиом? Следствия из аксиом стереометрии.
После обсуждения теоретических вопросов закрепление полученных знаний. Задание 1.Как в пространстве можно однозначно задать плоскость? Учащиеся самостоятельно выполняют задание (проверяем по плакату.) Способы задания плоскостей.
- Сколько существует способов задания плоскости? Пары обмениваются решениями и проверяют работы друг друга. Критерии: всё правильно – 3 балла, 1 ошибка– 2 балла, 2 ошибки– 1 балл, более 2 ошибок – 0 баллов. - Почему штатив фотоаппарата имеет три ножки, а не более? (Через три точки можно провести единственную плоскость) Задание 2. Ответьте на вопросы Сколько плоскостей можно провести через выделенные элементы? 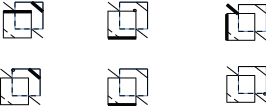 а) б) в) г) д) е) Ответы: а),б), в), г)- одна; д) – 2: е) - 3 Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение по чертежу на плакате. Критерии: всё правильно – 3 балла, 1 ошибка– 2 балла, 2 ошибки– 1 балл, более 2 ошибок – 0 баллов. Задание 3 Определите: верно, ли утверждение?
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение, сверяясь с плакатом на доске. Критерии: Всё правильно – 3 балла, 1 ошибка – 2 балла, 2 ошибки – 1 балл, более 2 ошибок – 0 баллов.  Дано: А, В, С α Доказать: D α Доказательство: А, В АВ, С,D СD, АВ СD, АВ, СD α D α Задание 4(3 балла)Три вершины параллелограмма лежат в некоторой плоскости. Можно ли утверждать, что и его четвертая вершина лежит в этой плоскости?  В С А D Блок– 2.Параллельные прямые в пространстве. Цель блока: - повторить и обобщить знания по теме параллельные прямые в пространстве; - систематизировать полученные знания. Актуализация опорных знаний. Проведем теоретическую разминку. Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. а - Взаимное расположение в пространстве двух прямых. 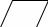 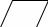   а в в в      а   а в а в а : в - Какие прямые в пространстве называются параллельными? (Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются) - Сформулируйте признак параллельности прямых в пространстве. (Две прямые, параллельные третьей прямой, параллельны). - Сформулируйте свойство параллельных прямых в пространстве. (Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну) - Какие прямые в пространстве называются скрещивающимися? (Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости и не пересекаются) Задание 1 Вставьте пропущенные слова (индивидуальные карточки) 1) Единственную плоскость можно задать через три точки, при этом они … на одной прямой. (не лежат) 2) Если … точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. (две) 3) Две различные плоскости могут иметь только одну общую … (прямую) 4) Прямые являются … в пространстве, если они не пересекаются и … в одной плоскости. (параллельными,лежат) 5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В  а, то прямые а и b …(скрещивающиеся) а, то прямые а и b …(скрещивающиеся)Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем. Критерии: Всё правильно – 3 балла, 1 ошибка– 2 балла, 2 ошибки– 1 балл, более 2 ошибок – 0 баллов. Задание 2 Определите: верно, ли утверждение?
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем. Критерии: всё правильно – 3 балла, 1, 2 ошибки– 2 балла, 3,4 ошибки– 1 балл, более 4 ошибок – 0 баллов. Задание 3Тест. 1.Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b? а) взаимное расположение точно определить нельзя; + б) скрещиваются или параллельны; в) параллельны или пересекаются; г) совпадают; д) пересекаются или скрещиваются. 2. Выберите верное утверждение. а) Две прямые называются параллельными, если они не имеют общих точек; б) две прямые, параллельные третьей прямой, параллельны; + в) две прямые, перпендикулярные третьей прямой, параллельны; 3. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда: а) прямые а и с пересекаются; б) прямая с лежит в плоскости α; в) прямые а и с скрещиваются; г) прямая b лежит в плоскости α; д) прямые а и с параллельны. + 4. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b? а) скрещиваются или пересекаются; б) пересекаются или параллельны; в) скрещиваются или параллельны; + г) только скрещиваются; д) только параллельны. 5. Если две прямые не скрещиваются, то они а) лежат в одной плоскости; + б) только пересекаются; в) совпадают; г) только параллельны. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение. Критерии: всё правильно – 3 балла, 1 ошибка– 2 балла, 2 ошибки– 1 балл, более 2 ошибок – 0 баллов. З Дано: ВС=АС, СС1 АА1, АА1=22 см Найти: СС1 Решение: АА1СС1, АС = ВС С1– середина А1В (по т.Фалеса) С С1- средняя линия ∆АА1В С С1= АА1 = 11 см Ответ: 11см. адание 4 Задача (3 балла) 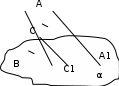 Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем. Блок – 3. Взаимное расположение в пространстве прямой и плоскости. Цель блока: - повторить и обобщить знания по теме взаимное расположение в пространстве прямой и плоскости; - систематизировать полученные знания. Актуализация опорных знаний. Проведем теоретическую разминку. Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. - Взаимное расположение в пространстве прямой и плоскости.  а   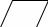 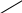 а 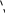 α α 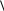 а α а α а α а α а α а α- Какие прямая и плоскость называются параллельными? (Прямая и плоскость называются параллельными, если они не пересекаются) - Сформулируйте признак параллельности прямой и плоскости в пространстве. (Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.) Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно. 1. Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга? а) параллельны + б) пересекаются + в) скрещиваются + 2. Прямые а и b параллельны. Через каждую из них проведено по плоскости, которые пересекаются по прямой с. Как расположена прямая с по отношению к прямым а и b? а) параллельно + б) пересекает в) перпендикулярно 3. Прямая а лежит в плоскости. Как расположена относительно плоскости прямая b, если b параллельна а? а) перпендикулярно б) параллельно + в) пересекает 4. Сколько плоскостей можно провести через две данные точки? а) одну б) две в) много + 5. Если одна из двух параллельных прямых пересекает плоскость, то другая прямая а) параллельна плоскости б) пересекает плоскость + в) перпендикулярна плоскости 7. Точка А принадлежит плоскости α, точка В не принадлежит плоскости α. Принадлежит ли плоскости середина отрезка АВ. а) да б) нет + в) не всегда 8. Прямая а параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение прямой а и плоскости . а) параллельны + б) пересекаются в) скрещиваются г) совпадают + Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем. Критерии: Всё правильно – 3 балла, 1, 2 ошибки– 2 балла, 3, 4 ошибки– 1 балл, более 3 ошибок – 0 баллов. A В С З  В адание 2 (3 балла) Плоскость проходит через сторону АС АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE α. Доказательство: 1. Точки D и E - середины отрезков АВ и BC соответственно 2. DE – средняя линия (по определению) DE АС (по свойству) DE α ( по признаку параллельности прямой и плоскости) D 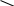 Е  А С α Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение во время обсуждения этих вопросов вместе с учителем. Задание 4(3 баллов) - дополнительное 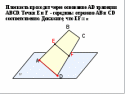 Доказательство: Точки Е и F - середины отрезков АВ и СD EF – средняя линия трапеции EF АD EF α (по признаку параллельности прямой и плоскости). Блок – 4. Взаимное расположение в пространстве двух плоскостей. Цель блока: - повторить и обобщить знания по теме взаимное расположение в пространстве двух плоскостей; - систематизировать полученные знания. Актуализация опорных знаний. Проведем теоретическую разминку. Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. - Взаимное расположение в пространстве двух плоскостей.         α     β α β  β α β α и β - совпадают α β - Какие плоскости называются параллельными? (Две плоскости называются параллельными, если они не пересекаются) - На практике в столовой, где встречаетесь с параллельными плоскостями? (Нарезка хлеба, при нарезке хлеба плоскость ножа остается в параллельных плоскостях. Газовая плита и кастрюли стоящие на ней. Плоскость газовой плиты должна быть параллельна плоскости пола (т.к. горизонтальной). Если это не будет выполнятся, жидкость из кастрюли будет выливаться.) - Сформулируйте признак параллельности плоскостей в пространстве. (Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны.) - Сформулируйте свойства параллельных плоскостей. 1. Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллельны. 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно. 1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение плоскостей α и . а) параллельны + б) пересекаются + в) совпадают + 2. Плоскость пересекает плоскости α и β по параллельным прямым а и в. Взаимное расположение плоскостей α и β. а) параллельны + б) пересекаются + в) совпадают 3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение плоскостей α и β. а) параллельны + б) пересекаются в) совпадают 4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение плоскостей α и β. а) параллельны + б) пересекаются + в) совпадают + Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение. Критерии: Всё правильно – 3 балла, 1 ошибки– 2 балла, 2 ошибки– 1 балл, более 2 ошибок – 0 баллов. Задание 2Верно ли, что
Учитель проверяет выполнение работы, обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем. Критерии: Всё правильно – 3 балла, 1, 2 ошибки– 2 балла, 3, 4 ошибки– 1 балл, более 4 ошибок – 0 баллов. З Решение. 1. В плоскости α возьмем т. В. 2. Проведем прямые ВС и ВD. 3. Построим вспомогательную плоскость через точку А и прямую ВD, в ней проведем прямую АD1 ВD. 4. Построим вспомогательную плоскость через точку А и прямую ВС, в ней проведем прямую АС1 ВС. 5. Через прямые АD1 и АС1 проведем плоскость β адание 3Задача 1. (3 балла) Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку А.    А D1 С1 β    В D С α Так как в плоскости АВС через точку А можно провести лишь одну прямую, параллельную ВС, а в плоскости АВD через точку А лишь одну прямую, параллельную BD, то задача имеет единственное решение. Следовательно, через каждую точку пространства можно провести единственную плоскость, параллельную данной плоскости. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение во время обсуждения этих вопросов вместе с учителем. Задание 4Задача 2. (3 балла) Доказать, что через каждую из двух скрещивающихся прямых можно провести плоскость так, чтобы эти плоскости были параллельны.    β в в1 Пусть а скрещивается с в. На прямой в возьмем т. А, через прямую а и т. А проведем плоскость, в этой плоскости через т. А проведем прямую в1 , в1 в. Через в1 в проведем плоскость α. Аналогично строим плоскость β. По признаку параллельности плоскостей α β. А    а а1 Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение во время обсуждения этих вопросов вместе с учителем. Тетради сдаются учителю для коррекции оценок. Учащиеся в это время выполняют самостоятельную работу. 3. Контроль знаний и способов действий Самостоятельная работа Задание общее, выполняется на подготовленных подписанных листочках. 1. Средняя линия трапеции лежит в плоскости α. Пересекают ли прямые, содержащие ее основания, плоскость α? (Нет, т.к. средняя линия трапеции параллельна основаниям. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости - признак параллельности прямой и плоскости в пространстве.) 2  в Доказательство: α β = а, в α, в β. Возьмем точку А а. Через А и в проведем плоскость . α = а, т.к. имеют общую точку А. в α в а . Докажите, что если данная прямая параллельна двум пересекающимся плоскостям, то она параллельна линии их пересечения    α     • а А . а а  β  Тем временем учитель проверяет работы учащихся и выставляет оценки. Оценки за самостоятельную работу объявляются на следующем уроке. 4. Подведение итогов урока. Молодцы! Трудились с полной отдачей, ощутили радость своего труда. Оценки получили: «5» - …, «4» - …, «3» - …. 5. Рефлексия. В конце урока учитель предлагает ученикам самим оценить свое настроение по результатам урока: 5- Мне всё понятно. Вопросов нет. 4- Мне почти всё понятно, но вопросы есть 3- Мне мало что понятно. Вопросов много. 2- Мне ничего не понятно. 6. Задание на дом. Домашнее задание зависит от качества работы на уроке. Если ученик отработал все учебные элементы и набрал максимальное количество баллов, то ему нет необходимости выполнять домашнее задание. Если же в ходе классной работы допускались ошибки, то рекомендуется повторить тот или иной учебный материал и решить оставшиеся задачи. Список литературы 1. Селевко Г.К. Современные образовательные технологии: Учебное пособие. - М.: ЮНИТИ-ДАНА, 1998. - 344с. 2. Голощёкина Л.П., Збаровский B.C. Модульная технология обучения: Методические рекомендации. - СПб: ЮНИТИ-ДАНА, 1993. - 135с. 3. Изучение геометрии 10-11 кл.: книга для учителя / С.М.Саакян, В.Ф. Бутузов. – М.: Просвещение, 2010. 4. Алтынов П.И. Геометрия. 10-11 класс. Тесты. 2001 5. Шарапова В.К. Тематические тесты по геометрии: 10-11 классы, Феникс, 2007 6. Лаппо Л.Д., Морозов А.В. Геометрия. Типовые вопросы и задачи – М.: «Экзамен», 2008. 7. Геометрия, 10—11 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2012 |