Аксиомы стереометрии. Р. 2. Тема 1 Аксиомы стереометрии. Аксиомы стереометрии Тема Что изучает стереометрия Аксиомы стереометрии. Цель урока
 Скачать 28.54 Kb. Скачать 28.54 Kb.
|
|
Раздел 2. Аксиомы стереометрии Тема 1. Что изучает стереометрия? Аксиомы стереометрии. Цель урока: Ознакомить учащихся с содержанием курса стереометрии; Изучить аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве. Задачи: обучающая: актуализация знаний по темам: «Параллельность прямых на плоскости», «Признаки параллелограмма», «Средняя линия треугольника», «Площади», «Решение треугольников по теореме косинусов», «Описанная окружность», знакомство с объектами изучения стереометрии, с их обозначениями и изображениями в пространстве, развивающая: способствовать развитию внимания, содействовать развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях, воспитательная: развивать у обучающихся коммуникативные компетенции (культуру общения, умение работать в группах). Оборудование: учебник «Геометрия 10-11», базовый и профильный уровни – учебник для общеобразовательных учреждений, Л.С. Атанасян., В.Ф.Бутузов, 18-е издание – М.: «Просвещение», 2014г. чертежные принадлежности; мультимедийная презентация «Введение в стереометрию. Аксиомы стереометрии», презентация Этапы урока: I. Организационный момент урока по теме: «Аксиомы стереометрии» 1-2 мин.) 1) Приветствие. 2) Проверка списочного состава обучающихся. 3) Сообщение темы и цели урока. II. Получение новых знаний (20 мин) В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости (на листе бумаги или на доске и т. д.). Таким образом, мы имели дело только с одной плоскостью, и все точки, линии, углы, вообще геометрические фигуры лежали только на ней. В курсе стереометрии нам предстоит рассматривать такие случаи, когда не все точки, линии и углы данной или данных фигур будут располагаться на одной плоскости. Будем считать, например, поверхность стола моделью плоскости Р; возьмем куб и поставим его одной гранью на стол. Легко видеть, что в данном кубе: 1) имеются точки, ребра, углы, лежащие на данной плоскости Р (на столе); 2) имеются точки, которые находятся вне плоскости Р; 3) имеются ребра, пересекающие плоскость Р; 4) имеются углы, находящиеся вне плоскости Р; 5) имеются шесть граней, являющиеся моделями шести различных плоскостей. Вывод. Плоскости могут вступать во взаимодействие с другими элементами фигур и друг с другом. Отсюда вытекает необходимость изучать различные случаи комбинаций плоскостей между собой, комбинации плоскостей с линиями и другими геометрическими объектами. Это изучение является одной из задач курса стереометрии. В первую очередь надо выяснить основные свойства плоскостей по отношению друг к другу, к точкам и прямым. Введем обозначения: точки – А, В, С и т. д. прямые – a, b, с и т. д. или (АВ, СD и т. д.) плоскости – α, β, γ и т. д.     Основные свойства плоскости. Всем знакома ситуация: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, то есть опирается на три «точки», а конец четвертой ножки (четвертая «точка») не лежит в плоскости пола, а висит в воздухе. Этот пример служит наглядным подтверждением того факта, что через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Так как три точки, не лежащие на одной прямой, однозначно определяют плоскость, то можно обозначать плоскость как (АВС), (BCD) и т. д. Можно ли провести плоскость через три точки, лежащие на одной прямой? Сколько существует таких плоскостей? Верно ли, что: а) любые три точки лежат в одной плоскости; б) любые четыре точки лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость, и притом только одна? Ответы: а) да; б) нет; в) нет; г) нет. Рассмотрим следующую ситуацию: для проверки «ровности» при укладке тротуарной плитки используют брусок, который прикладывают к поверхности дорожки. Если на дорожке есть ложбинки или бугорок, то в каких-то местах между бруском и плоскостью дорожки образуется просвет. Если поверхность дорожки ровная, то между бруском и дорожкой никакого просвета нет, то есть брусок всеми своими точками прилегает к ее поверхности. Можно встретить и обратную ситуацию, когда проверяют «ровность» линейки при помощи проверенной модели плоскости. Эти примеры служат наглядным подтверждением того факта, что если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Верно ли, что прямая лежит в плоскости данного треугольника, если она: а) пересекает две стороны треугольника; б) проходит через одну из вершин треугольника? Ответ обоснуйте. Обратимся к модели куба. Обучающимся предлагается на модели куба указать: 1) точку, принадлежащую одновременно двум данным пересекающимся граням; 2) точку, принадлежащую трем данным пересекающимся граням; 3) грани, которым принадлежит точка, взятая на каком-нибудь ребре куба; 4) грани, которым принадлежит данная вершина куба. Вывод. Точка, лежащая на линии пересечения двух плоскостей, лежит на каждой из этих плоскостей, и обратно: точка, лежащая одновременно на двух каких-нибудь плоскостях, лежит на линии пересечения этих плоскостей. На вопрос, что является линией пересечения двух плоскостей (в теоретико-множественном смысле: если прямые имеют хотя бы одну общую точку), отвечает третья аксиома: если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через данную точку. Наглядной иллюстрацией третьей аксиомы является пересечение двух смежных сторон классной комнаты, пересечение двух листов книги и т. д. Могут ли две пересекающиеся плоскости иметь общую точку, не принадлежащую линии пересечения этих плоскостей? Прямые а и b пересекаются в точке С. Через прямую а проходит плоскость α, а через прямую b – плоскость β, отличная от α. Как проходит линия пересечения этих плоскостей? Следует обязательно отметить, что в пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии. III. Закрепление новых знаний (15 минут) № 9 (перечертите чертеж и ответы запишите с помощью символики). Постройте изображение куба АВСDА1В1С1D1: 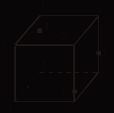 а) назовите плоскости, в которых лежат точка М, точка N; б) найдите точку F – точку пересечения прямых MN и ВС. Каким свойством обладает точка F? (Принадлежит и прямой MN, и плоскости (АВС)); в) найдите точку пересечения прямой KN и плоскости (АВС). IV. Информация о домашнем задании (1-2 мин) теория (п. 1 – 2), № 1 (перечертите чертеж и ответы запишите с помощью символики), №№ 3, 10, 12, 13. V. Рефлексия(1-2 мин) |
