|
|
урок геометрии 8 класс. урок 54_1. Урока по геометрии 54 Ф. И. О. учителя Класс 8 Тема урока Теорема об отрезках пересекающихся хорд Тип урока комбинированный урок Цели урока
Технологическая карта урока по геометрии №54
1.Ф.И.О. учителя:
2. Класс: 8
3. Тема урока: Теорема об отрезках пересекающихся хорд
4.Тип урока: комбинированный урок
5. Цели урока:
Деятельностная: развитие у обучающихся способностей к самостоятельному выявлению и исправлению своих ошибок на основе рефлексии коррекционно-контрольного типа: умение фиксировать собственные затруднения, выявлять их причину, строить и реализовывать проект выхода из затруднения.
Образовательная: познакомиться с теоремой об отрезках пересекающихся хорд и сформировать навыки по её применению для решения задач; сформировать систему новых понятий, расширить знания учеников за счет включения новых определений, терминов, описаний, следствий, теорем.
6. Задачи урока:
Образовательная: систематизировать теоретические знания по теме: “Центральные и вписанные углы” и совершенствовать навыки решения задач по данной теме; сформулировать и доказать теорему об отрезках пересекающихся хорд; применить теорему при решении геометрических задач, обучать особенностям решения задач с использованием вписанных и центральных углов.
Развивающая: развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;
Коммуникативные: (владение всеми видами речевой деятельности и основам культуры устной речи, умеют оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения и следовать им).
Интеллектуальные: (анализ, оценивание, классификация, обобщение).
Информационные: (умение извлекать информацию из текста учебника, применять).
Организационные: (умение формулировать цель деятельности, планировать ее достижение, осуществлять самооценку).
Воспитательные: воспитание трудолюбия, усердия в достижении цели, интерес к предмету
7.Методы и приемы обучения: частично-поисковый, проблемный, наглядный: просмотр презентации; методы контроля: выполнение заданий с самопроверкой.
8.Средства обучения:
Учебник
Рабочая тетрадь к учебнику;
9.Оборудование: мультимедийный проектор, экран, компьютер.
10.Планируемые результаты обучения:
Предметные:пользоваться геометрическим языком для описания предметов окружающего мира (окружность, полуокружность, центральный угол, точки пересечения, центр окружности, вписанные углы, градусная мера дуги, радиус, диаметр); распознавать геометрические фигуры, различать их взаимное расположение (прямая и окружность, центральные и вписанные углы); изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур.
Метапредметные:Познавательные: учащиеся должны обнаруживать и формулировать учебную проблему совместно с учителем; осуществлять самооценку и самокоррекцию учебной деятельности, саморефлексию; уметь понимать точку зрения другого, слушать; Регулятивные: умеют определять и формулировать цель на уроке; проговаривать последовательность действий на уроке; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки, планировать свои действие в соответствии с поставленной задачей;
Личностные:способность осуществлять самооценку на основе критерия успешности учебной деятельности, обучающиеся должны объяснять самому себе свои отдельные ближайшие цели саморазвития, понимать и осознавать социальную роль ученика; проявлять положительное отношение к урокам математики, интерес к способам решения новых учебных задач, понимать причины успеха или неуспеха в своей учебной деятельности.
Структура урока деятельностной направленности.
Этапы урока
|
Деятельность учителя
|
Деятельность учащихся
|
Оргмомент
|
Приветствие, выявление отсутствующих, проверка готовности к уроку.
|
Подготовка к работе
|
Актуализация знаний и проверка умений
|
Билет №1
Дайте определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Запишите формулу суммы углов выпуклого многоугольника
Докажите теорему о средней линии треугольника.
Р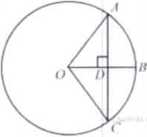 адиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей. Найдите длину хорды АС, если BD = 1 см, а радиус окружности равен 5 см. адиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей. Найдите длину хорды АС, если BD = 1 см, а радиус окружности равен 5 см.
Периметр прямоугольника равен 56, а диагональ равна 20. Найдите площадь этого прямоугольника.
|
Билет №2
Д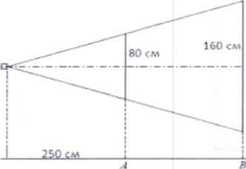 айте определение и свойства параллелограмма. айте определение и свойства параллелограмма.
Докажите свойство медиан треугольника
П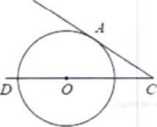 роектор полностью освещает экран А высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными? роектор полностью освещает экран А высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.
|
Билет №3
Дайте определение и назовите свойства прямоугольника.
Д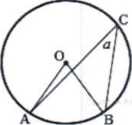 окажите теорему Пифагора. окажите теорему Пифагора.
Найдите величину (в градусах) вписанного угла а, опирающегося на хорду АВ, равную радиусу окружности.
Прямая, параллельная основаниям МР и MN трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и КР в точках А и В соответственно. Найдите длину отрезка АВ, если МР = 40см, NK = 24см.
|
Билет №4
Дайте определение и назовите свойства ромба.
Докажите теорему о вписанном угле (любой частный случай).
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?
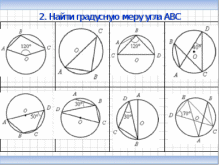
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
|
Билет №10
Дайте определение вписанного и центрального углов окружности.
Билет №4
2. Докажите теорему о вписанном угле (любой частный случай).
|
Выполняют задания
Устная работа
|
Изучение нового материала
|
Решить задачу 1 с целью подготовки учащихся к восприятию нового материала
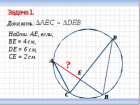 
АЕ = 3 см
Вопросы для обсуждения
Что вы можете сказать об углах CAB и CDB?
Об углах AEC и DEB?
Какими являются треугольники ACE и DBE?
Чему равно отношение их сторон, являющихся отрезками хорд касательных?
Какое равенство можно записать из равенства двух отношений, используя основное свойство пропорции?
Попробуйте сформулировать утверждение, которое вы доказали. На доске и в тетрадях записать формулировку и конспект доказательства теоремы об отрезках пересекающихся хорд. К доске вызывается один человек
Билет №15
2. Докажите свойство отрезков пересекающихся хорд.
|
Познакомься с необходимым для урока теоретическим материалом.

|
Закрепление
|
№ 667 на доске
Решение.
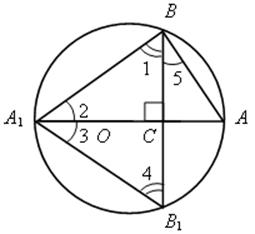
1) 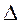 АВА1 – прямоугольный, так как вписанный угол А1ВА опирается на полуокружность. АВА1 – прямоугольный, так как вписанный угол А1ВА опирается на полуокружность.
2) 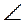 5 = 5 = 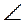 3 как вписанные и опирающиеся на одну дугу АВ1. 3 как вписанные и опирающиеся на одну дугу АВ1.
3) 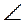 1 = 90° – 1 = 90° – 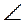 5, 5,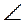 4 = 90°– 4 = 90°– 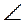 3, но 3, но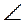 3 = 3 = 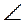 5, поэтому 5, поэтому 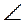 1= 1= 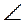 4. 4.
4) 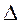 А1ВВ1 – равнобедренный, тогда ВС = В1С. А1ВВ1 – равнобедренный, тогда ВС = В1С.
5) По теореме о произведении отрезков пересекающихся хорд
АС · А1С = ВС · В1С.
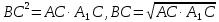
6) 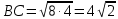 (см); (см); 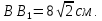
Ответ: 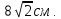
Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.
Решение.
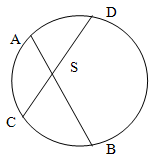
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS ∙ SB = CS ∙ SD, тогда
2х ∙ 3х = 5 ∙ 12
6х2 = 60
х2 = 10
x = √10.
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
Ответ: 5√10
|
Решают задачи
|
Итог урока. Д/З
|
Подведение итогов урока, мобилизация учащихся на самооценку своей деятельности;
- Итак, что вы узнали сегодня на уроке?
- Чему научились сегодня на уроке?
- Оцени свою деятельность за урок по 5 – бальной системе.
Выставление отметок за урок.
п. 71 (выучить теорию),
№ 659, 661, 666 (б, в).
|
Работа с дневниками
| |
|
|
 Скачать 1.14 Mb.
Скачать 1.14 Mb.
 адиус
адиус  айте определение и свойства параллелограмма.
айте определение и свойства параллелограмма. роектор полностью освещает экран
роектор полностью освещает экран  окажите теорему Пифагора.
окажите теорему Пифагора.



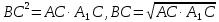
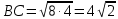 (см);
(см);