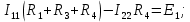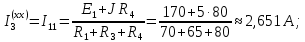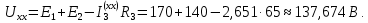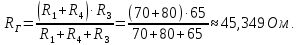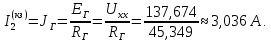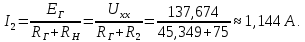Электротехника - ИДЗ - исследование линейных цепей. ИДЗ1. Условия расчетнографических работ
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
Условия расчетно-графических работ ЗАДАНИЕ №1 Линейные электрические цепи с постоянными напряжениями и токами Для своего варианта и заданной схемы с постоянными во времени источниками ЭДС и тока, принимая 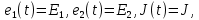 выполнить следующее: 1. Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления. Для всех вариантов принять J = 5 А. 2. Записать систему уравнений для определения токов во всех ветвях схемы и напряжения на зажимах источника тока по законам Кирхгофа. Составить баланс вырабатываемой и потребляемой мощностей. 3. Определить токи во всех ветвях: методом контурных токов, методом узловых потенциалов. 4. Составить баланс вырабатываемой и потребляемой мощностей. 5. Рассматривая цепь относительно сопротивления R2 ветви ab с источником ЭДС 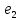 как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в данной ветви, построить внешнюю характеристику эквивалентного генератора и по ней графически определить ток в этой же ветви. как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в данной ветви, построить внешнюю характеристику эквивалентного генератора и по ней графически определить ток в этой же ветви.6. Сравнить результаты вычислений, оценить трудоемкость методов расчета и сформулировать выводы по выполненным пунктам задания.
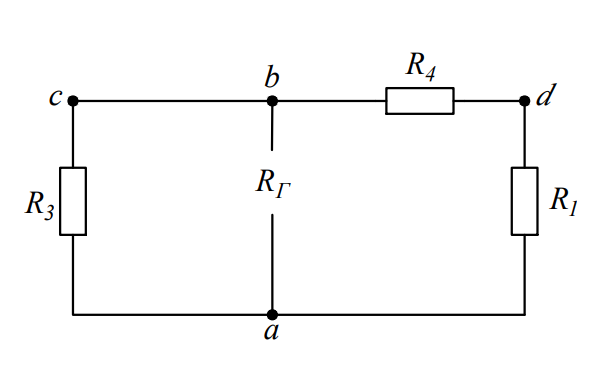
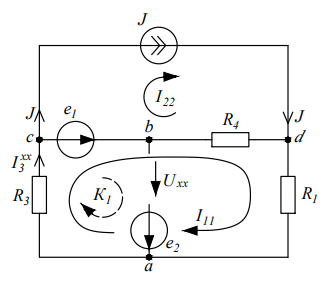
Изменение схемы для проведения расчетов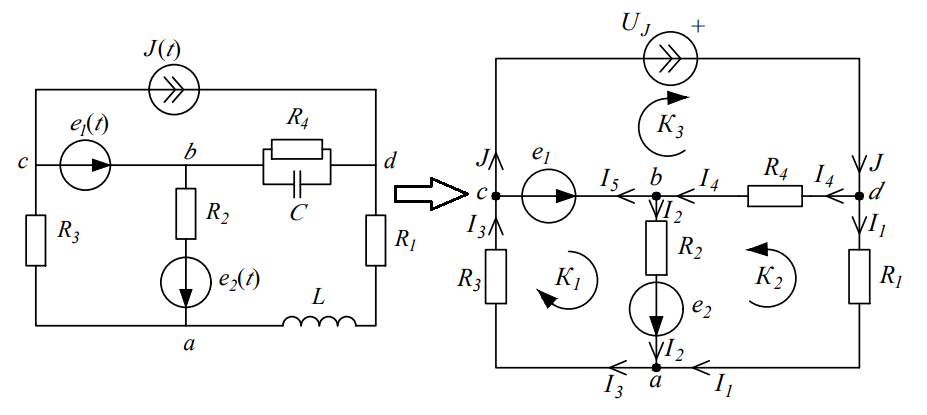 Рисунок 1 – Исходная и измененная схемы Схема изменяется с учетом того, что в ней протекает постоянный ток, для которого индуктивность L является закороткой, а конденсатор C – разрывом ветви. Также на схеме указываются направления обходов контуров и направления токов для составления уравнений по правилам Кирхгофа, токи нумеруются.
Токи ветвей и напряжение на источнике тока по правилам КирхгофаОпределяется необходимое число уравнений, составляются сами уравнения: По первому правилу: 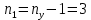 . По второму правилу: . По второму правилу: 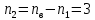 . .
Составляется система линейных алгебраических уравнений: 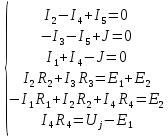 Решение полученной системы линейных алгебраических уравнений находится при помощи программы Mathcad. Полученные значения заносятся в таблицу 4.
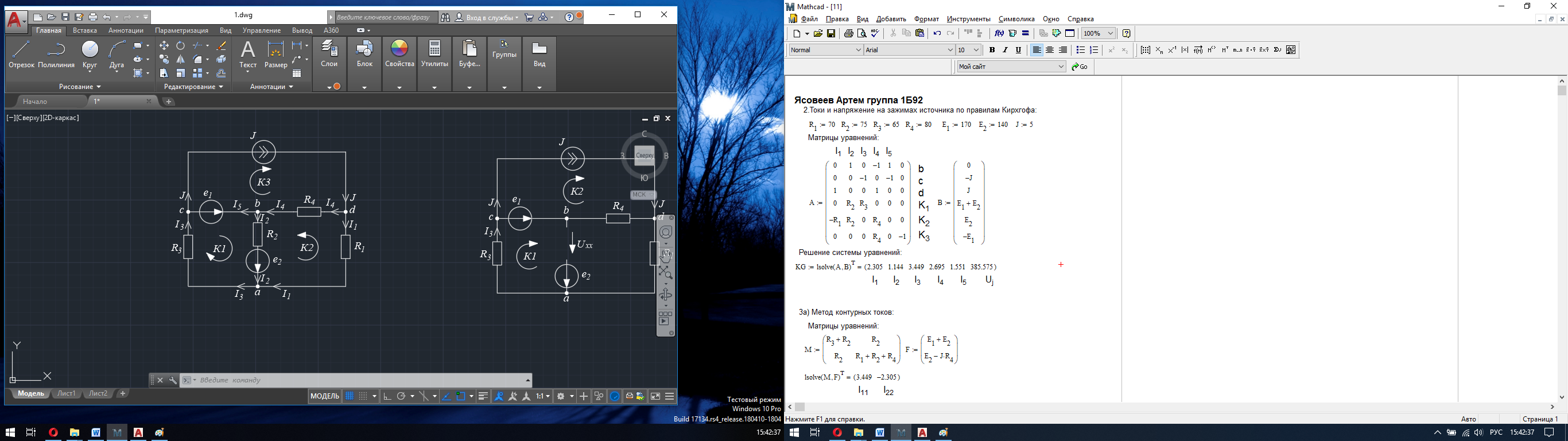 Рисунок 2 – Расчет по правилам Кирхгофа в Mathcad Найденные величины проверяются подстановкой в исходные уравнения.
Величины удовлетворяют уравнениям. Баланс мощностей выполнен однократно в пункте 4 – значения токов, полученных разными методами, совпадают. Расчет токов по методу контурных токов и методу узловых потенциаловМетод контурных токов
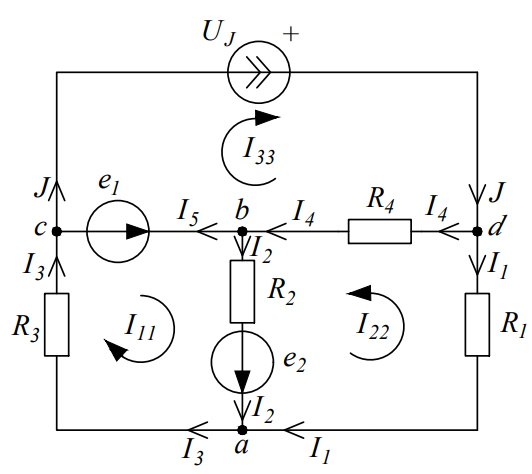 Рисунок 3 – Схема для расчета по МКТ Пусть в независимых контурах согласно направлениям на схеме текут контурные токи 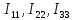 . Контур №3 содержит источник тока, поэтому . Контур №3 содержит источник тока, поэтому 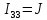 . .Для контуров №1 и №2 составляются уравнения:
Решение данной системы уравнений находится при помощи Mathcad: 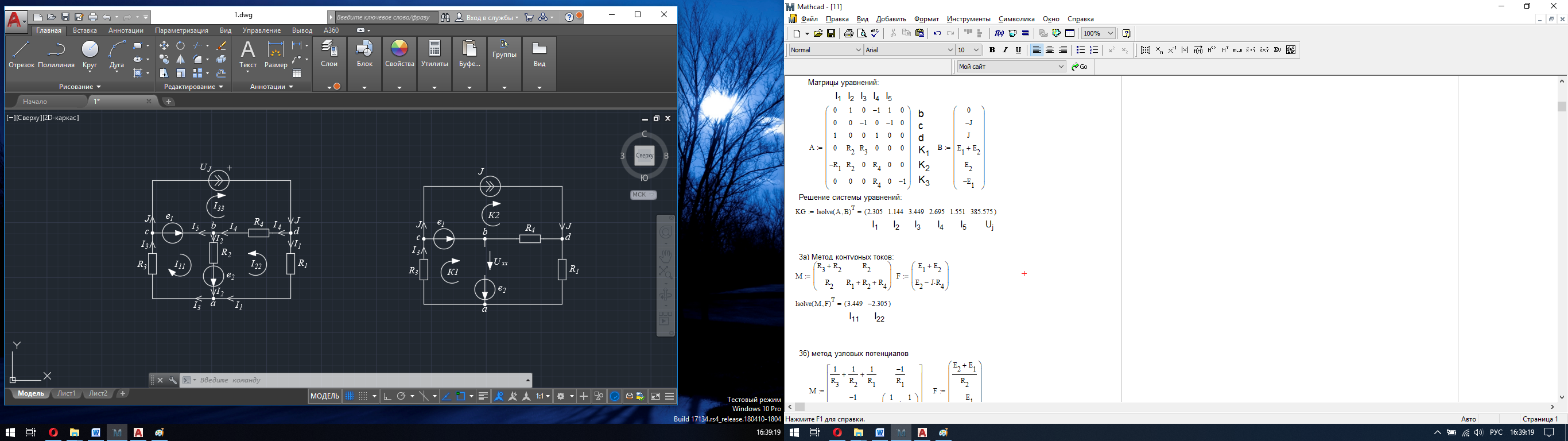 Рисунок 4 – Решение системы уравнений Составляются выражения для определения значений реальных токов:
Рассчитанные токи совпадают с токами, полученными в пункте 2. Метод узловых потенциалов 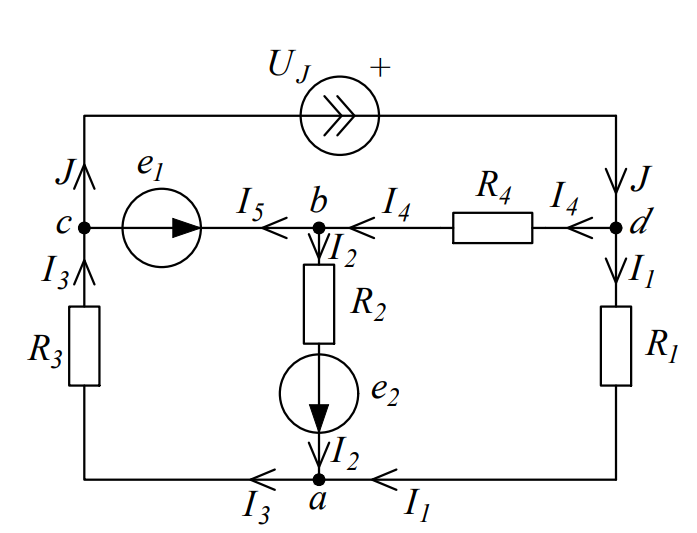 Рисунок 5 – Схема для расчета по методу узловых потенциалов Ветвь cb содержит только источник ЭДС e1, тогда узел c заземляется и его потенциал 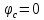 , а потенциал узла b в таком случае , а потенциал узла b в таком случае 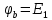 . .Для потенциалов узлов aи dсоставляются расчетные уравнения:
Система уравнений решается в программе Mathcad: 
Потенциал 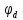 равен напряжению на источнике тока, полученное значение совпадает со значением, найденным в пункте 2. равен напряжению на источнике тока, полученное значение совпадает со значением, найденным в пункте 2.По обобщенному закону Ома составляются выражения для расчета токов.
Найденные значения токов совпадают со значениями из пунктов 2 и 3а. Баланс вырабатываемой | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 11 – Параметры эквивалентного генератора | ||
| Ток генератора, 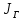 | ЭДС генератора, 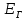 | Сопротивление ген., 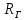 |
| 3,036 A | 137,674 B | 45,349 Oм |
По параметрам эквивалентного генератора строится его внешняя ВАХ, на диаграмму также помещается ВАХ резистора
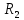 , точка пересечения будет решением.
, точка пересечения будет решением.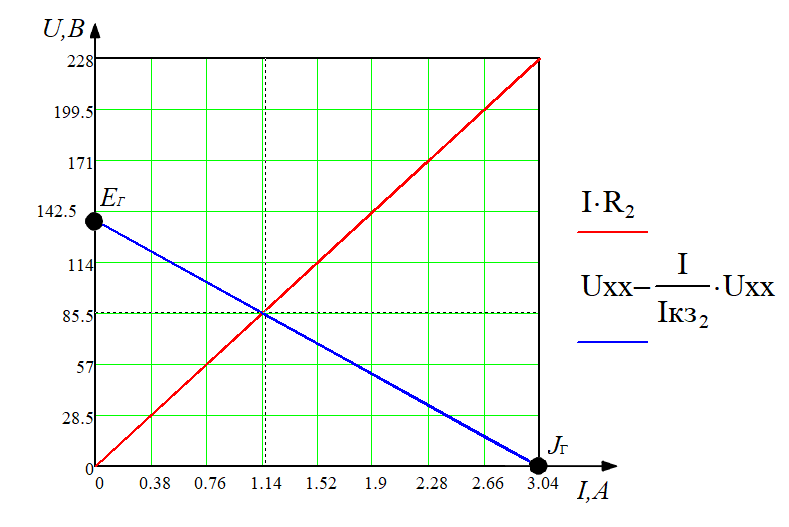
Рисунок 8 – Диаграмма ВАХ
В точке пересечения напряжение
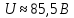 , а сила тока
, а сила тока 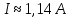 . Результаты графического метода согласуются с результатами аналитического метода, кроме того, результаты обоих методов согласуются с результатами пунктов 2 и 3.
. Результаты графического метода согласуются с результатами аналитического метода, кроме того, результаты обоих методов согласуются с результатами пунктов 2 и 3.Выводы
В ходе работы различными методами определены токи ветвей, а также напряжение на выводах источника тока некоторой электрической цепи. Значения, полученные разными методами, совпали. Следовательно, любой из методов даёт результат с приблизительно одинаковой точностью.
Несмотря на то, что методы дают одинаковые результаты, их трудоемкость сильно разнится. Наиболее трудоемким является метод с использованием правил Кирхгофа, так как он требует решения сложных систем уравнений, зато он позволяет получить все неизвестные величины разом. В отличие от него, метод эквивалентного генератора позволяет путем несложных вычислений определить ток в одной конкретной ветви. В случае, когда ветвей несколько, его применение будет нецелесообразно, так как придется выполнять большое количество однообразных расчетов. Менее трудоемкими являются метод контурных токов и метод узловых потенциалов. Метод контурных токов сводит процесс расчета к решению несложных систем уравнений, но он не позволяет определять потенциалы узлов. Метод узловых потенциалов позволяет определять как потенциалы, так и токи путем решения несложных систем уравнений, но его недостаток в том, что он не позволяет определить силу тока ветви, если она не содержит сопротивлений (ветвь cb), в таком случае приходится прибегать к правилам Кирхгофа.
Каждый из рассмотренных методов имеет свои достоинства и недостатки, поэтому выбор оптимального в конкретной ситуации метода необходимо осуществлять с учетом особенностей задачи.

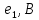
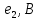
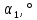
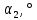
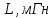
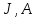
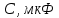
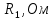
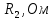
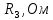
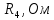
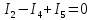
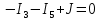
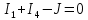
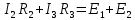
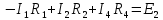
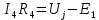
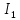
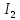
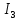
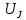
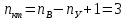
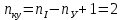
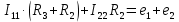
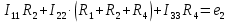
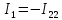
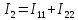
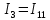
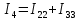
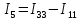
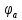
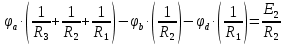
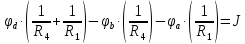
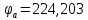 В
В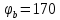 В
В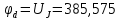 В
В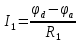
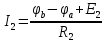
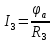
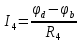
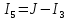
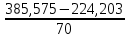
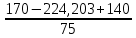
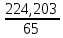
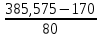
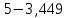
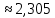 А
А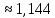 А
А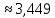 А
А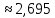 А
А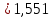 А
А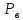 и потребляемой
и потребляемой 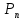 мощности:
мощности: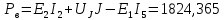 Вт;
Вт;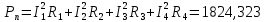 Вт.
Вт.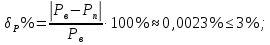
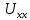 направляется так же, как и ток
направляется так же, как и ток 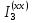 .
.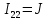 , так как в данном контуре присутствует источник тока.
, так как в данном контуре присутствует источник тока.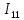 :
: