Курс на Си. Подбельский. Курс программирования на Си. В., Фомин С. С. Курс программирования на языке Си Учебник
 Скачать 1.57 Mb. Скачать 1.57 Mb.
|
1'-)Для решения этой задачи определим функцию: float w(float g, float h) { if ( g >= h ) return 3.14159*g*g*h; else return 3.14159*g*h*h; } Для возврата из функции и передачи результата в точку вызова в теле функции используются два оператора return. Функция для вычисления скалярного произведения векторов. Скалярное произведение двух векторов n-мерного линейного пространства вычисляется по формуле s = E«A. /=1 Функция для вычисления указанного произведения может быть определена следующим образом: /* Скалярное произведение n-мерных векторов */ float Scalar_Product (int n, float a[ ], float b[ ]) { int i; /* Параметр цикла */ float z; /* Формируемая сумма */ for (i=0, z=0.0; i z+=a[i]*b[i]; return z; /* Возвращаемый результат */ } Первый параметр n специфицирован как целая переменная типа int. В спецификации массивов-параметров типа float пределы изменения индексов не указаны, что позволяет при обращении к функции использовать вместо a и b в качестве аргументов одномерные массивы такого же типа любых размеров (с любым количеством элементов). Конкретные пределы изменения их индексов задает аргумент, заменяющий параметр int n. Обращение к функции и ее прототип. Как уже говорилось, для обращения к функции используется элементарное (первичное) выражение, называемое «вызов функции»: имя_функции (список_аргументов) Значение этого выражения - возвращаемое функцией значение (определяется в теле функции выполненным оператором return). Список аргументов - это список выражений, заменяющих параметры функции. Соответствие между параметрами и аргументами устанавливается по порядку их расположения в списках. Если параметров у функции нет, то не должно быть и аргументов при обращении к этой функции. Аргументы передаются из вызывающей программы в функцию по значению, то есть вычисляется значение каждого аргумента, и именно оно используется в теле функции вместо заменяемого параметра. Пример вызова определенной выше функции для вычисления объема цилиндра: w(z-1.0,1e-2) Стандарт языка Си предусматривает обязательное описание функции с помощью прототипа. Прототип имеет формат: тип_результата имя_функции (спецификация_ параметров); Здесь спецификация параметров представляет собой список типов и, возможно, имен параметров функции. Прототип функции схож с ее заголовком. Но имеются два существенных отличия. Во-первых, прототип всегда заканчивается признаком конца оператора (символ «;»). Во-вторых, в прототипе могут не указываться имена специфицируемых параметров. Прототип может не использоваться только в том случае, когда определение функции находится в том же файле, где размещена вызывающая ее программа, и это определение помещено в тексте выше вызывающей программы. Прототипы введенных выше функций могут быть такими: float w(float, float); Scalar_Product ( int n, float a[ ], float b[ ]); Имена параметров в прототипе функции w( ) не указаны, специфицированы только их типы. Прототипы функций необходимо размещать наряду с определением объектов в теле функций до исполняемых операторов. Приведем примеры программ, состоящих более чем из одной функции. Вычисление биномиального коэффициента. Как известно, где n > m > 0; n, m - целые. Составим программу для вычисления биномиального коэффициента, в которой используем функцию для вычисления факториала: #include int fact(int k) /* Вычисление факториала k!*/ { int j, i; /* Вспомогательные переменные */ for(i=1, j=1; i<=k; i++) /*Цикл вычисления*/ j*=i; return j; } /* Конец определения функции */ /* Вычисление биномиального коэффициента: */ void main( ) { int n, m, nmc, nm; /*nm - значение (n-m) */ /* nmc - значение биномиального коэффициента */ while (1) { printf("\nBeegume n="); scanf("%d",&n); printf("Beegume m="); scanf("%d", &m); if (m>=0 && n>=m && n<10) break; printf("Ошибка! Необходимо 0<=m<=n<10"); } nm=n-m; nmc=fact(n)/fact(m)/fact(nm); printf ("\n Биномиальный коэффициент=%б", nmc); } /* Конец основной программы */ В основной программе прототип функции fact( ) не нужен, так как определение функции находится в том же файле, что и функция main( ), вызывающая fact( ), причем определение размещено выше вызова. Пример выполнения программы: Введите n=4 Введите m=5 Ошибка ! Необходимо 0 Введите n=4 Введите m=2 Биномиальный коэффициент =6 Вычисление объема цилиндра с использованием приведенной выше функции w( ): #include /* Вычисление объема цилиндра: */ void main( ) { float w(float, float); /* Прототип функции */ float a,b; /* Исходные данные */ int j; /* Счетчик попыток ввода */ for (j=0; j<5; j++) { /* Цикл ввода данных */ printf("\n Введите a="); scanf("%f",&a); printf(" Введите b="); scanf("%f",&b); if ( a > 0.0 && b > 0.0 ) break; printf("\n Ошибка, нужно a>0 и b>0!\n"); } if (j == 5) { printf("\n ОЧЕНЬ ПЛОХО вводите данные!!"); return; /* аварийное окончание программы*/ } printf("\n Объем цилиндра =%f", w(a,b)); } /* Конец основной программы */ /*Функция для вычисления объема цилиндра: */ float w(float g, float h) { if ( g >= h ) return(3.14159*g*g*h); else return(3.14159*g*h*h); } В основной программе использован оператор return, прерывающий исполнение программы. Оператор return выполняется после цикла ввода исходных данных, если количество неудачных попыток ввода (значений a и b) равно 5. Задан прототип функции w( ), то есть задан ее прототип, что необходимо, так как она возвращает значение, отличное от int, и определена стандартным образом позже (ниже), чем обращение к ней. Обращение к функции w( ) использовано в качестве аргумента функции printf( ). Пример выполнения программы:
Вычисление площади треугольника. Для определения площади треугольника по формуле Герона s = 7p(p-^)(p-b)(p-c) достаточно задать длины его сторон А, В, С и, вычислив полупериметр р=(А+В+С)/2, вычислить значение площади по формуле. Однако для составления соответствующей программы необходима функция вычисления квадратного корня. Предположив, что такой функции в библиотеке стандартных математических функций нет, составим ее сами. В основу положим метод Ньютона: xt = (xi-1 + z/x--1)/2, i = 1, 2, ... где z - подкоренное выражение; x0 - начальное приближение. Вычисления будем проводить с фиксированной относительной точностью е. Для простоты условием прекращения счета будет вы- значения введем еще одну функцию с именем abs( ) (хотя такая функция, так же как функция для вычисления квадратного корня, есть в стандартной библиотеке). Программа может быть такой:    полнение неравенства *,-i #include { float a,b,c,p,s; float sqr(float); /* Прототип функции */ printf("\n Сторона a= "); scanf("%f",&a); printf("Сторона b= "); scanf("%f",&b); printf("Сторона c= "); scanf("%f",&c); if(a+b <= c || a+c <= b || b+c <= a) { printf("\n Треугольник построить нельзя!"); return; /* Аварийное окончание работы */ } p=(a+b+c)/2; /* Полупериметр */ s=sqr(p*(p-a)*(p-b)*(p-c)); printf("Площадь треугольника: %f",s); } /* Конец основной программы */ /* Oпределение функции вычисления квадратного корня */ float sqr(float x) { /* x-подкоренное выражение */ /*Прототип функции вычисления модуля: */ float abs(float); double r,q; const double REL=0.00001; /* REL-относительная точность */ if (x < 0.0) { printf("\n Отрицательное подкоренное" " выражение"); exit(1); /* Аварийное окончание программы */ } if (x == 0.0) return x ; /* Итерации вычисления корня: */ r=x; /* r - очередное приближение */ do { q=r; /* q - предыдущее приближение */ r=(q+x/q)/2; } while (abs((r-q)/r) > REL); return r; } /* Конец определения функции sqr */ /* Определение функции */ /* для получения абсолютного значения: */ float abs(float z) { if(z > 0) return z; else return(-z); } /* Конец определения функции abs */ В программе используются три функции. Основная функция main( ) вызывает функцию sqr( ), прототип которой размещен выше вызова. Функция abs( ) не описана в основной программе, так как здесь к ней нет явных обращений. Функция abs( ) вызывается из функции sqr( ), поэтому ее прототип помещен в тело функции sqr( ). В процессе выполнения программы может возникнуть аварийная ситуация, когда введены такие значения переменных a, b, c, при которых они не могут быть длинами сторон одного треугольника. При обнаружении подобной ситуации выдается предупреждающее сообщение «Треугольник построить нельзя!», и основная функция main( ) завершается оператором return. В функции sqr( ) также есть защита от неверных исходных данных. В случае отрицательного значения подкоренного выражения (x) нужно не только прервать вычисление значения корня, но и завершить выполнение программы с соответствующим предупреждающим сообщением. Оператор return для этого неудобен, так как позволяет выйти только из той функции, в которой он выполнен. Поэтому вместо return; при отрицательном значении x в функции sqr( ) вызывается стандартная библиотечная функция exit( ), прекращающая выполнение программы. Прототип (описание) функции exit( ) находится в заголовочном файле stdlib.h, который включается в начало текста программы пре- процессорной директивой. Пример результатов выполнения программы: Сторона a=2.0 Сторона b=3.0 Сторона c=4.0 Площадь треугольника: 2.904737 Скалярное произведение векторов. Выше была определена функция Scalar_Product( ) для вычисления скалярного произведения векторов, в которой параметрами являлись массивы. Следующая программа использует эту функцию: /* Скалярное произведение векторов */ #include #define MAX_INDEX 5 void main( ) { /* Прототип функции: */ float Scalar_Product(int, float[ ], float[ ]); int n,i; float x[MAX_INDEX],y[MAX_INDEX]; printf("\n Размерность векторов n= "); scanf("%d",&n); if(n < 1 || n >MAX_INDEX) { printf("\n Ошибка в данных!"); return; /* Аварийное завершение */ } printf("Введите %d координ. x: ",n); for (i=0; i printf("Введите %d координ. y: ",n); for (i=0; i printf("\n Результат: %7.3f", Scalar_Product(n,x,y)); } /* Определение функции scalar: */ float Scalar_Product(int n, float a[],float b[]) /* Скалярное произведение n-мерных векторов */ /* n - размерность пространства векторов */ /* a[ ],b[ ] - массивы координат векторов */ { int i; /* Параметр цикла */ double z; /* Формируемая сумма */ for (i=0,z=0.0; i < n; i++) z += a[i]*b[i]; return z; /* Возвращаемый результат */ } В начале программы с помощью #define введена препроцессор- ная константа MAX_INDEX. Далее определены массивы, у которых пределы изменения индексов заданы на препроцессорном уровне. Именно эти пределы проверяются после ввода размерности векторов (n). В теле функции main( ) приведен прототип функции Scalar_Product( ). Обратите внимание, что в прототипе отсутствуют имена параметров. Тот факт, что два параметра являются одномерными массивами, отображен спецификацией float[]. Результаты выполнения программы: Размерность векторов n=2 Введите 2 координ. x: 1 3.1 Введите 2 координ. y: 1 2.1 Результат: 7.510 Другая попытка выполнить программу: Размерность векторов n=0 Ошибка в данных! Диаметр множества точек. Как еще один пример использования функций с массивами в качестве параметров рассмотрим программу определения диаметра множества точек в многомерном евклидовом пространстве. Напомним, что диаметром называется максимальное расстояние между точками множества, а расстояние в евклидовом пространстве между точками x = { xi }; y = { yi }, i = 1, ..., n, определяется как d(x, y) = л | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Количество | точек к=4 | |
| Размерность | пространства n=3 | |
| Введите 3 | координ. точки 1: | |
| 1 1 | 1 | |
| Введите 3 | координ. точки 2: | |
| -1 -1 | -1 | |
| Введите 3 | координ. точки 3: | |
| 2 2 | 2 | |
| Введите 3 | координ. точки 4: | |
| -2 -2 | -2 | |
Результат:
Диаметр = 6.928203
Номера точек: 3, 4
В программе особый интерес представляет обращение к функции distance( ), где в качестве аргументов используются индексированные элементы a[i], a[m]. Каждый из них, по определению, есть одномерный массив из n элементов, что и учитывается в теле функции. Для задания размеров массива a[ ][ ] и предельных значений переменных k и n используются препроцессорные константы K_MAX и
N_MAX. Их нельзя определить как переменные, то есть ошибочной будет последовательность:
int K_MAX=100; N_MAX=10; float a[K_MAX][N_MAX];
При определении массивов их размеры можно задавать только с помощью константных выражений.
Переключатели
Основным средством для организации мультиветвления служит оператор-переключатель, формат которого имеет вид:
switch( выражение )
case константа1: операторы_1;
case константа2: операторы_2;
default: операторы;
}
В этом операторе используются три служебных слова: switch, case, default. Первое из них идентифицирует собственно оператор- переключатель. Служебное слово case с последующей константой является в некотором смысле меткой. Константы могут быть целыми или символьными и все должны быть различными (чтобы метки были различимы). Служебное слово default также обозначает отдельную метку. При выполнении оператора (рис. 2.6а) вычисляется выражение, записанное после switch, и его значение последовательно сравнивается с константами, которые помещены вслед за case. При первом же совпадении выполняются операторы, помеченные данной меткой. Если выполненные операторы не предусматривают какого-либо перехода (то есть среди них нет ни goto, ни return, ни exit( ), ни break), то далее выполняются операторы всех следующих вариантов, пока не появится оператор перехода или не закончится переключатель.
Операторы вслед за default выполняются, если значение выражения в скобках после switch не совпало ни с одной константой после case. Метка default может в переключателе отсутствовать. В этом случае при несовпадении значения выражения с константами переключатель не выполняет никаких действий. Операторы, помеченные меткой default, не обязательно находятся в конце (после других вариантов переключателя). Уточним, что default и «case константа»
не являются метками в обычном смысле. К ним, например, нельзя перейти с помощью оператора goto.
На рис. 2.6 приведены схемы переключателя (рис. 2.6а) и оператора альтернативного выбора или селектора (рис. 2.6 б), отсутствующего в языке Си.
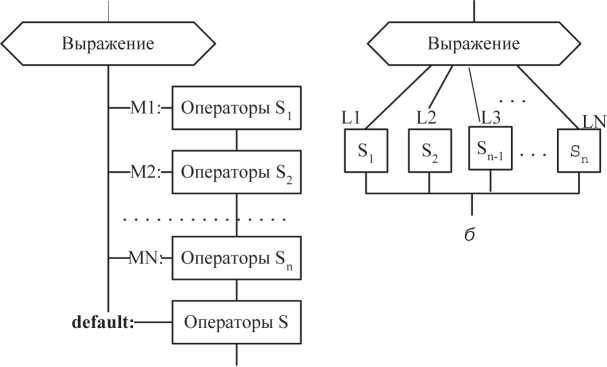
а
Рис. 2.6. Переключатель (а) и альтернативный выбор (б): а - если выражение равно МК, то выполняются операторы Sk, Sk+1...S, S;
б - если выражение равно LK, то выполняются т,.о..,лько операторы Sk
На рис. 2.7 изображена схема альтернативного выбора, реализованная при помощи переключателя и операторов перехода (go to, return, break), введенных в S1, S2, ..., Sn.
Для иллюстрации работы переключателя рассмотрим программу, которая читает десятичную цифру и выводит на экран ее название:
#include
{
int i;
while(1)
{
printf("\n Введите десятичную цифру: ");
scanf("%d",&i);
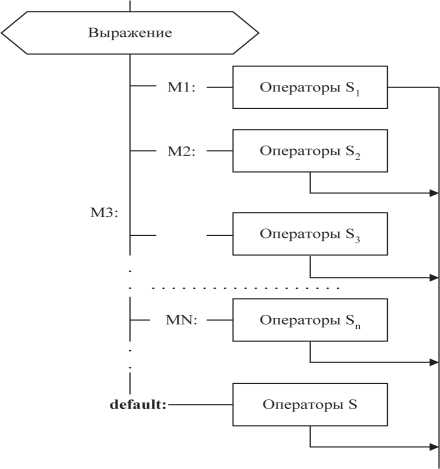
Рис. 2.7. Альтернативный выбор с использованием переключателя. В число операторов каждой группы Skдобавлен оператор выхода из переключателя
| printf("\t\t"); switch( i ) f | ||
| 1 case 1: | printf("%d - | один \n",i); |
| break; case 2: break; | printf("%d - | два \n",i); |
| case 3: | printf("%d - | три \n",i); |
| break; case 4: break; | printf("%d - | четыре \n",i) |
| case 5: | printf("%d - | пять \n",i); |
| break; case 6: break; | printf("%d - | шесть \n",i); |
| case 7: | printf("%d - | семь \n",i); |
| break; case 8: break; | printf("%d - | восемь \n",i) |
case 9: printf("%d - девять \n",i);
break;
case 0: printf("%d - нуль \n",i);
break;
default: printf("%d - это не цифра! \n",i); return;
} /* Конец переключателя */
} /* Конец цикла */
}
Пример результатов выполнения программы:
| Введите | десятичную | цифру: 3 3 - три | |
| Введите | десятичную | цифру: 8 8 - восемь | |
| Введите | десятичную | цифру: -7 -7 - это не цифра! | |
Программа прекращает выполнение, как только будет введен символ, отличный от цифры. Завершение программы обеспечивает оператор return; который в данном случае передает управление операционной системе, так как выполняет выход из функции main( ).
Переключатель вместе с набором операторов break реализует в этой программе альтернативный выбор (см. рис. 2.7). Если удалить все операторы break, то работа переключателя в этой программе будет соответствовать схеме рис. 2.6а.
Несколько «меток» case с разными значениями констант могут помечать один оператор внутри переключателя, что позволяет еще больше разнообразить схемы построения операторов switch.
Контрольные вопросы
Можно ли написать завершенную программу без функции main()?
Какое расширение должно иметь имя файла с текстом программы на языке Си?
Назовите обязательные этапы обработки, которые проходит исходная программа, подготовленная на языке Си в виде текстового файла.
Объясните роль препроцессора при подготовке программы на языке Си.
Какие требования существуют в отношении препроцессорных директив?
Каким образом включают в программу прототипы библиотечных функций?
Какова структура простой программы на языке Си?
Для чего служат библиотечные функции?
Назовите состав тела функции.
Для чего служат определения и описания?
Как можно задать комментарий в тексте программы?
Перечислите группы операторов языка Си.
Какие операторы применяются для управления работой программы?
Чем отличается блок от составного оператора?
В каких местах кода программы может быть поставлена метка?
Как обозначается пустой оператор?
Перечислите операторы циклов языка Си.
Перечислите операторы ветвлений языка Си.
В чем сходства и различия операторов break и continue?
Что представляет собой инициализация объекта (например, массива)?
Значения каких типов могут возвращать функции?
Как задается имя неглавной функции?
Дайте определение списка параметров.
С помощью какого оператора производится возврат из функции в точку ее вызова?
Что такое прототип функции?
Где размещают прототипы функций?
Каким образом организуется мультиветвление в программе на языке Си?
Чем отличаются действия переключателя и оператора альтернативного выбора?
