Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
12.2. Метрологические характеристики,предназначенные для определениярезультатов измеренийФункция преобразования F(X). Данная функции нормируется для измерительных преобразователей и приборов с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины. Она задается в виде формулы, таблицы или графика и используется для определения значений измеряемой величины X в рабочих условиях применения СИ по известному значению информативного параметра его выходного сигнала: X = F-1(Y), где F-1 — функция, обратная функции преобразования; Y — показания средства измерений; Для стандартизованных СИ серийного производства нормируют номинальную функцию преобразования. Для приборов мелкосерийного производства нормируют индивидуальные функции преобразования. Для стандартизованных СИ, конструктивные особенности которых обуславливают существенный разброс индивидуальных функций преобразования, нормируют пределы (граничные значения), в которых они должны находиться при заданных условиях. Для линейных функций преобразования, проходящих через начало координат, может нормироваться номинальный или индивидуальный коэффициент преобразования. Значение Y однозначной или значение Y многозначной меры. Для этих характеристик нормируются номинальные или индивидуальные значения. Они используются для устройств, применяемых в качестве мер. Например, у нормального элемента нормируется номинальное значение генерируемой им электродвижущей силы, у кварцевого генератора — значение частоты его колебаний и т.д. Цена деления шкалы измерительного прибора или многозначной меры. Нормирование цены деления производится для показывающих приборов с равномерной шкалой, функция преобразования которых отображается на именованной шкале. При неравномерной шкале нормируется минимальная цена деления. Характеристики цифрового кода, используемого в СИ и их элементах. К ним относятся: вид выходного кода, число его разрядов, цена единицы младшего разряда. Эти характеристики нормируются для цифровых приборов. 12.3. Метрологические характеристикипогрешностей средств измеренийЭта группа характеристик описывает погрешности, обусловленные собственными свойствами СИ в нормальных условиях эксплуатации. Суммарное их значение образует основную погрешность СИ. Характеристики систематической составляющей погрешности. Эти характеристики отражают свойства совокупности СИ данного типа (а не отдельного экземпляра) и описываются либо только значением систематической составляющей 0S, либо его математическим ожиданием М[0S] и СКО [0S]. Нормировать последние две величины целесообразно в том случае, если можно пренебречь их изменениями как во времени, так и под влиянием других величин. Подход к определению систематической составляющей погрешности, регламентированный ГОСТ 8.009—84, несколько отличается от общепринятого. Обычно под систематической погрешностью понимают постоянную или закономерно изменяющуюся детерминированную (неслучайную) величину. Если же из физических соображений ясно, что некоторая составляющая погрешности постоянна или закономерно изменяется, т.е. по определению является систематической, но ее значение неизвестно, а известны лишь пределы, в которых она может находится, то учитывать эту погрешность можно лишь как случайную величину, каким-то образом распределенную в заданных пределах. Природа "случайности" обусловлена не объективными причинами формирования погрешности, а ограниченностью наших знаний и технических возможностей. Поэтому принципы нормирования систематической погрешности должны быть такими же, как и для случайной погрешности. Такой подход объясняется еще и тем, что характеристики систематической погрешности нормируются для большой совокупности СИ данного типа. При этом погрешности каждого конкретного прибора уже объективно являются частными реализациями случайно распределенной (по экземплярам) величины. Характеристики систематической составляющей нормируются путем установления пределов допускаемой систематической погрешности osp = М[0S]+Кр[0S], где КР — коэффициент, определяемый законом распределения погрешности и принятым значением доверительной вероятности. Могут также нормироваться МО М[0S] и СКО [0S]. Эти величины характеризуют разброс систематической составляющей по совокупности экземпляров СИ данного типа и при необходимости позволяют приближенно учесть его. Характеристики случайной составляющей погрешности. Под случайной составляющей инструментальной погрешности ̊0 понимается случайная составляющая погрешности СИ, обусловленная только его собственными свойствами. Она представляет собой центрированный случайный процесс и описывается либо СКО [̊0], либо СКО совместно с нормализованной автокорреляционной функцией г() или функцией спектральной плотности S(). Характеристики случайной составляющей нормируются путем установления предела допускаемого СКО. Возможно нормирование номинальной нормализованной автокорреляционной функции или номинальной функции спектральной плотности, а также пределов их отклонения от номинальных. Характеристика случайной составляющей погрешности от гистерезиса. Эта характеристика называется вариацией выходного сигнала СИ. Она представляет собой основание закона распределения случайной составляющей погрешности от гистерезиса. Под случайной составляющей погрешности от гистерезиса ̊он понимается случайная составляющая погрешности СИ, обусловленная отличием показаний данного экземпляра измерительного прибора от информативного параметра входного сигнала при различных скорости и направлении его изменения. Характеристика случайной составляющей погрешности от гистерезиса нормируется путем установления предела Н0р допускаемой вариации выходного сигнала (показания) СИ. Выбор перечисленных MX основной погрешности в качестве нормируемых сделан [7, 58] на основе математической модели, в которой основная погрешность СИ рассматривается как нестационарный случайный процесс 0(t): 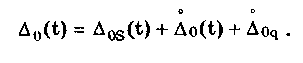 (12.1) (12.1)Физический смысл величин, входящих в формулу, следующий. Систематическая составляющая os(t) включает в себя постоянные и настолько медленно (в том числе и случайно) изменяющиеся во времени погрешности, что их изменением за время проведения измерений можно пренебречь. Частотный спектр погрешности os(t) лежит в инфранизкочастотной области. Она описывается МО M[os], СКО [os] и пределом допускаемых значений osp. В этих характеристиках не отражена нестационарность погрешности СИ, которая отнесена к систематической составляющей. При необходимости характеристики M[Dos] и [Dos] могут выражаться как функции времени, однако такое представление нецелесообразно в большинстве случаев, так как привело бы к практически не реализуемым методам испытаний. Составляющая D̊0q является центрированной случайной величиной, и ее параметры неизменны во времени. Она включает в себя составляющие случайной погрешности, не вошедшие в Dos (t) и D0(t), например погрешность квантования. Случайный стационарный эргодический процесс D0(t) описывает временные изменения погрешности СИ, которые группируются вокруг Dos(t). Погрешность D0(t), как правило, имеет широкий и неравномерный частотный спектр, в котором целесообразно выделить две типичные составляющие: D̊0H(t) — высокочастотную, имеющую такой спектр, что ее интервал корреляции заведомо меньше времени отдельного измерения; D̊0L(t)— низкочастотную, имеющую спектр, лежащий между спектрами составляющих D̊0H(t) и Dos Удобство такого разделения погрешности D̊0(t) обусловлено тем, что при оценке характеристик инструментальных составляющих в общем случае необходимо знать автокорреляционную функцию основной погрешности СИ. Очевидно, что подход к определению автокорреляционных функций разных составляющих уравнения (12.1) должен быть различным. Реализации погрешностей D̊0H(t) и D̊0q(t) для отдельных измерений всегда некоррелированы, и для них находить автокорреляционные функции не нужно, достаточно определить дисперсию. Аналогично нет необходимости вычислять автокорреляционную функцию систематической составляющей Dos(t), поскольку она практически постоянна в течение измерений. Для составляющей D̊0L(t) следует определять автокорреляционную функцию. Учитывая все сказанное выше, уравнение (12.1) можно записать в виде: 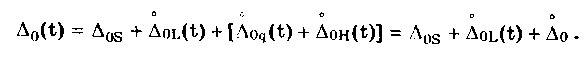 (12.2) (12.2)Данная модель включает: Dos — систематическую погрешность, представляющую собой настолько медленно изменяющийся случайный процесс, что в течение продолжительности обычных измерений ее можно считать постоянной. Она описывается пределом допускаемых значений Dosp; D̊0L(t) коррелированную случайную погрешность, которая описывается автокорреляционной функцией R() или спектральной плотностью S(). Вместо R() могут нормироваться нормализованная автокорреляционная функция r() и СКО [D̊0L(t)]; D̊0 — некоррелированную случайную погрешность, которая описывается дисперсией В рассмотренной модели инструментальной погрешности не учтены гистерезисные явления, вызывающие вариацию показаний. При их учете основная погрешность должна быть записана в виде 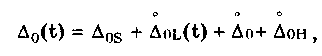 (12.3) (12.3)где D̊0H — случайная составляющая, обусловленная гистерезисом и аналогичными явлениями и подчиняющаяся равномерному закону распределения в пределах некоторого интервала, называемого вариацией. Для этой погрешности нормируется вариация Нор. Уравнение (12.3) представляет собой окончательную математическую модель основной погрешности средства измерений. ГОСТ 8.009—84 допускает при малой случайной погрешности производить нормирование составляющих не отдельно, а в целом погрешности СИ, включая случайную составляющую от гистерезиса. Если известны нормированные значения характеристик составляющих инструментальной погрешности M[Dos], [Dos], [D̊0] и Нор , то пределы, в которых с заданной вероятностью лежит основная погрешность любого экземпляра СИ данного типа, определяется формулой 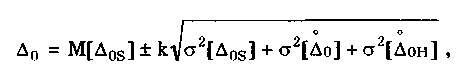 где k — коэффициент, значение которого зависит от доверительной вероятности. При 0,8 < Р < 1 он может быть рассчитан по формуле k = 5(Р - 0,5). Более точные значения коэффициента приведены в руководящем нормативном документе РД 50-453—84. Дисперсия вариации 2[D̊0L(t)] = H20p /12, так как случайная погрешность от гистерезиса имеет равномерный закон распределения в пределах от 0 до Н0Р. Если нормированные значения М[Dos] и [Dos] не заданы, а известно нормированное значение Dosp, то основная погрешность 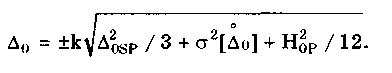 Здесь учтено, что систематическая составляющая погрешности распределена по равномерному закону в пределах ± Dosp. Использование первой формулы дает более точный результат по сравнению со второй формулой за счет более полного учета статистических свойств систематической составляющей погрешности. Это обуславливается тем, что использование М[Dos] и [ Dos] для расчета не требует знания закона распределения систематической погрешности. При использовании же для расчета величины Аддр желательно знать закон ее распределения, однако он, как правило, не известен, вследствие чего приходится считать его равномерным. Это и приводит к завышенным расчетным оценкам интервалов для основной погрешности. 12.4. Характеристики чувствительности средствизмерений к влияющим величинам.Неинформативные параметры выходногосигналаВлияние, оказываемое внешними факторами, описывается при помощи следующих характеристик. Функция влияния () — это зависимость изменения MX средства измерений от изменения влияющей величины или их совокупности в рабочих условиях применения СИ. Использование функций влияния позволяет определить не предельно возможные значения погрешности, практически не встречающиеся при исправных СИ, а их статистические оценки. Нормирование функции производится путем установления ее номинального значения и пределов допустимых отклонений от него. Возможно нормирование граничных, верхней и нижней функций влияния. Изменения значений метрологических характеристик СИ, вызванные изменениями влияющих величин в установленных пределах, () — это разность (без учета знака) между MX, соответствующей некоторому заданному значению влияющей величины ; в пределах рабочих условий применения СИ, и данной MX, соответствующей нормальному значению влияющей величины. Эти изменения нормируются путем установления пределов допускаемых изменений характеристики при изменении влияющей величины в заданных пределах. Дополнительная погрешность СИ вызывается изменениями влияющих величин относительно своих нормальных значений и, следовательно, является их функцией. Для различных экземпляров СИ одного типа могут значительно меняться как вид функции, так и ее параметры. Однако для всех СИ того или иного типа эти функции должны быть подобны, а их параметры близки. Поэтому в качестве основной характеристики дополнительной погрешности принята некоторая средняя (номинальная) для данного типа функция зависимости погрешности от изменения влияющих величин. Функции влияния могут нормироваться как отдельно для каждой влияющей величины, так и для определенной их совокупности. Нормирование совместных функций целесообразно и необходимо в тех случаях, когда существенны эффекты взаимовлияния величины на характеристики погрешностей. Влияющие величины могут вызывать изменения не только погрешности, но и других MX средства измерений. Поэтому для таких случаев целесообразно предусмотреть нормирование соответствующих функций влияния. Функция Y(x) устанавливает связь между статистическими характеристиками дополнительной погрешности с СИ и изменением влияющей величины: = - 0 , где и 0 — текущее значение влияющей величины в реальных условиях применения СИ и ее нормированное значение соответственно. Математическое ожидание (систематическая составляющая) и СКО дополнительной погрешности имеют вид: М[Dс] = Ds(); [Dс] = (), где Ds и - функции влияния величины на систематическую погрешность и СКО случайной погрешности СИ. При необходимости функция влияния на вариацию нормируется отдельно. В этом случае характеристики погрешности конкретного СИ выражаются следующим образом (для простоты считается, что вариация равна нулю): 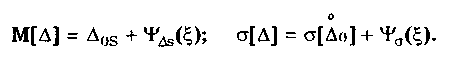 Данные формулы справедливы в том случае, когда изменения влияющих величин являются известными детерминированными функциями. Если же учитываются как случайные величины или функции, обладающие своими математическими ожиданиями и дисперсиями, то последние формулы должны быть записаны в виде 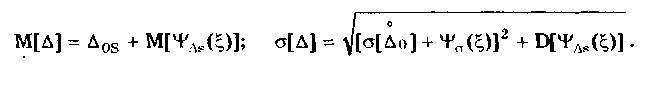 Это особенно важно для функции влияния Ds(), поскольку влияющие величины обычно вызывают значительные изменения именно систематической погрешности. В данном случае функция влияния Ds() характеризуется своим математическим ожиданием М[Ds()] и дисперсией D[Ds()]. Учет влияния случайного разброса величин Dx на дисперсию или СКО, путем введения соответствующих функций D() и (), привел бы к тому, что их необходимо было бы учитывать как случайные величины. И поэтому сама случайная погрешность СИ должна была бы рассматриваться как случайная функция с очень сложным видом нестационарности. Все это привело бы к практически непреодолимым трудностям при оценке погрешностей. В то же время значения Dx влияют на характеристики случайной погрешности значительно меньше, чем на систематическую погрешность. Этот дает основание пренебречь влиянием разброса величин Dx на дисперсию случайной погрешности и рассматривать функции влияния YD(x) и Ys(x) как детерминированные. При проведении расчетов рекомендуется учитывать только те значения аргументов Dx, при которых данные функции влияния имеют максимальные значения — Ys(x)max. Для функции влияния нормируются ее вид и параметры. Характеристики аргумента Dx при расчетах определяются исходя из реальных условий эксплуатации СИ. При этом знания только предельных значений Dx недостаточно. Необходимо иметь информацию как о центре группирования, так и о степени ее разброса. Функции влияния могут иметь самый разный вид. В простейшем случае они являются линейными: YDs(x) = А, где А — постоянная величина. В этом случае М[Dx] = АМ[Dx]; D[YDs(x)] = А2 D[Dx], где М[Dx] и D[Dx] — математическое ожидание и дисперсия величины Dx соответственно. Наиболее просто дополнительные погрешности рассчитываются для СИ, у которых функции влияния различных внешних величин (температуры, влажности, напряжения питания и т.д.) взаимно независимы. На практике возможны ситуации, когда имеет место взаимная зависимость функций влияния нескольких величин 1, 2, 3, ..., L. В этом случае нормируют функцию совместного влияния (1, 2, 3, ..., L), которая и используется при расчетах дополнительной погрешности. Неинформативные параметры выходного сигнала (см. рис. 12.1) являются одним из видов влияющих величин и определяют допустимую область значений тех параметров выходного сигнала, которые не содержат непосредственной информации о значении измеряемой величины. Однако они определяют возможность нормальной работы СИ. Неинформативные параметры выходного сигнала СИ нормируют путем установления номинальных значений и пределов допускаемых отклонений от них. 12.5. Нормирование динамических характеристиксредств измеренийВ состав нормальных условий, при которых определяется основная погрешность, входит определенный частотный спектр входного сигнала или конкретная функция спектральной плотности. Для СИ, частотный диапазон которого охватывает нулевую частоту, основная погрешность, как правило, определяется при неизменном во времени входном сигнале. Такая погрешность является статической. Если информативный параметр входного сигнала изменяется во времени в заданной полосе частот, то в качестве частотного спектра нередко принимают определенную частоту из этой полосы. Найденная при этом основная погрешность будет квазистатической. Любое отличие частотного спектра входного сигнала от принятого вызывает динамическую погрешность. Выделение этих погрешностей практически целесообразно тогда, когда изменение частотного спектра входного сигнала СИ приводит к существенному изменению точности. Это означает, что для одного и того же СИ при каком-либо одном частотном спектре входного сигнала нужно учитывать динамическую погрешность, а при другом в этом нет необходимости. Решение вопроса о том, учитывать погрешность как статическую (квазистатическую) или как динамическую, зависит не только от частотного спектра входного сигнала. Важным фактором является также соотношение между отличием частотного Спектра от нормального и инерционностью СИ. Именно это соотношение определяет уровень динамической погрешности по отношению к статической. Для описания динамических погрешностей используются следующие характеристики: 1. Полная динамическая характеристика аналоговых СИ, в качестве которой используют одну из характеристик: переходную, импульсную переходную, амплитудно-фазовую, амплитудно-частотную, совокупность амплитудно-частотной и фазочастотной, передаточную функцию. Все они подробно рассмотрены в разд. 11.3. Полную динамическую характеристику нормируют путем установления номинальной и пределов допускаемых отклонений от нее. Нормировать следует такую характеристику, которая может быть относительно просто определена экспериментально. 2. Частные динамические характеристики аналоговых СИ, которые можно использовать как линейные. К ним относятся время реакции, коэффициент демпфирования, постоянная времени и др. 3. Частные динамические характеристики АЦП и цифровых измерительных приборов, время реакции которых не превышает интервала между двумя измерениями, соответствующего максимальной частоте (скорости) измерений, а также ЦАП. К ним относятся время реакции, погрешность датирования отсчета, максимальная частота измерений и др. Под частной динамической характеристикой СИ понимается функционал или параметр полной динамической характеристики. 4. Динамические характеристики аналого-цифровых СИ, время реакции которых больше интервала меяуду двумя измерениями, соответствующего максимально возможной для данного типа средств измерений частоте (скорости) измерений. К ним относятся полные динамические характеристики эквивалентной аналоговой части аналого-цифровых СИ, погрешность датирования отсчета, максимальная частота (скорость) измерений и др. Под временем реакции понимается: • для показывающего измерительного прибора — время установления показаний; • для ЦАП или многозначной управляемой меры — время, прошедшее с момента подачи управляющего сигнала до момента, начиная с которого выходной сигнал преобразователя или меры отличается от установившегося значения не более, чем на заданное значение; • для АЦП и цифрового измерительного прибора — время, прошедшее с момента скачкообразного изменения измеряемой величины в сторону возрастания и одновременной подачи сигнала запуска до момента, начиная с которого показания цифрового прибора или выходной код АЦП отличаются от установившего показания или значения выходного кода на величину, не превышающую заданное значение. Погрешностью датирования отсчета АЦП или цифрового измерительного прибора называется случайная величина — интервал времени, начинающийся в момент начала цикла преобразования (запуска) АЦП или прибора и заканчивающийся в момент, когда значения изменяющихся измеряемой величины и выходного цифрового сигнала на данном цикле преобразования оказались равны. При этом значения выходного цифрового сигнала АЦП и показания цифрового измерительного прибора выражены в единицах измеряемой величины. Эта погрешность обусловлена наличием времени задержки запуска АЦП, временем автоматического определения полярности измеряемого сигнала, временем выбора пределов измерения, временем преобразования и т.п. При измерении (преобразовании) постоянной во времени величины погрешность датирования отсчета равна нулю. В отличие от полных частные характеристики не позволяют вычислить динамическую составляющую погрешности измерений. Используя их, можно лишь приближенно сопоставить свойства СИ с условиями измерений. Частные динамические характеристики нормируют путем установления номинальных характеристик и пределов допускаемых отклонений от них. Для ЦАП и многозначных мер может нормироваться переходная характеристика или время реакции, поскольку при использовании таких СИ обычно необходимо знать, через какое время после подачи сигнала управления можно считывать установившееся значение выходной величины. Особую группу СИ составляют АЦП, у которых выходной сигнал изменяется дискретно в соответствии с управляющей частотой дискретизации. Как правило, в этих устройствах все переходные процессы и процесс преобразования заканчиваются за время, которое меньше минимального интервала дискретизации. Поэтому для них часто достаточно нормировать время реакции. При длительных переходных процессах во входных цепях, когда время реакции АЦП больше минимального интервала между двумя измерениями, целесообразно нормировать динамические характеристики только аналоговой части АЦП, т.е. такие же, как для аналоговых СИ. Пример 12.1. Для средств измерений температуры характерным динамическим свойством является тепловая инерция, поэтому большинство из них представляют собой динамические звенья первого порядка. Их динамические MX нормируются путем указания номинальных переходной и импульсной переходной функций и допустимых отклонений от них. Номинальные функции могут задаваться аналитическими выражениями 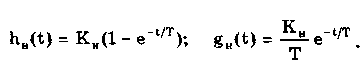 где Кн — номинальный статический коэффициент преобразования. Однако ввиду сложности подбора аналитического выражения чаще их задают графически, как показано на рис. 12.2. Допустимые от номинальных функций отклонения могут быть представлены различными способами: • заданием аналитических выражений, описывающих верхнюю (hHmax(t) и gнmax(t) на pис. 12.2) и нижнюю (hHmin(t) и gHmin(t) на рис. 12.2) допустимые границы для значений нормируемой функции. Если вид временной зависимости, описывающей границы значений нормируемой функции, отличается от нее самой только значениями коэффициента Кн, то могут нормироваться допустимые отклонения его значений Кнmах и Kнmin; • построением графических зависимостей hHmax(t), gHmax(t), hHmin(t) и gHmin(t) (см.рис. 12.2), описывающих верхнюю и нижнюю допустимые границы для значений нормируемой функции; • указанием допустимых отклонений + и _ от номинальной функции в отдельные моменты времени. 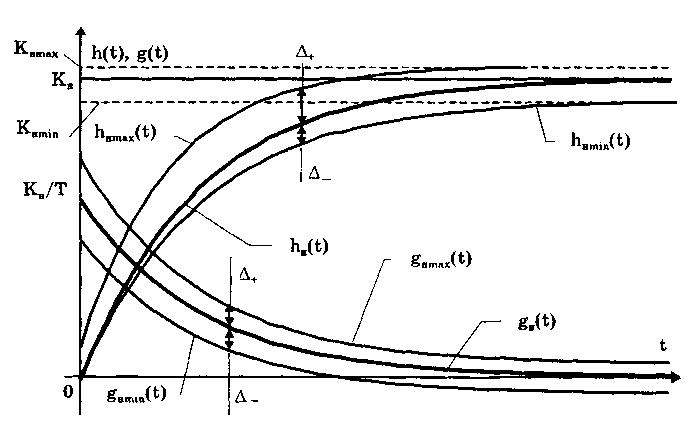 Рис. 12.2. Номинальные переходная и импульсная переходная функции и допустимые отклонения от них, указанные различными способами 12.6. Метрологические характеристики влиянияна инструментальную составляющуюпогрешности измеренияК указанным характеристикам относятся характеристики СИ, отражающие их способность влиять на инструментальную составляющую вследствие взаимодействия СИ с любым из подключенных к его входу или выходу компонентов, например объектом измерений и др. Потребление энергии средством измерений от объекта измерения или от предвключенного прибора приводит к изменению значения измеряемой величины и, следовательно, к появлению соответствующей составляющей погрешности. Например, на погрешность измерения температуры с помощью термопар и термометров существенно влияет обмен тепловой энергией между объектом и прибором. Следовательно, для СИ, работа которых характеризуется обменом энергией между ними и подключенными к их входу или выходу объектами, необходимо нормировать некоторые характеристики, описывающие свойства этих приборов отбирать или отдавать энергию через свои входные или выходные цепи. Такие характеристики часто называют импедансными, или просто импедансами. Вопросы нормирования импедансов средства измерений электрических величин разработаны достаточно полно. Сложнее обстоит дело с приборами для измерений неэлектрических величин, где явления обмена энергией, входные и выходные импедансы изучены недостаточно. В этом случае нормирование требует тщательных исследований. Рассматриваемые характеристики нормируются путем установления номинальных значений импедансных характеристик и пределов допускаемых отклонений от них. Конкретные способы оценки составляющих, обусловленных взаимодействием СИ с объектом измерений, зависят"от характера этого взаимодействия и вида импедансной характеристики. В практике электрических измерений достаточно распространен случай, когда взаимодействие заключается в потреблении средством измерений энергии от объекта измерений и когда соответствующее свойство описывается входным импедансом. Эквивалентная схема подключения СИ к объекту измерения показана на рис.12.3. По условиям измерительной задачи необходимо измерить ЭДС E(j), записанную в комплексной форме. Объект измерения, обладающий выходным импедансом Z0(j), подключен к СИ через линию связи, имеющую эквивалентное сопротивление Zлс(j). Средство измерений на схеме представлено в виде параллельного соединения его входного импеданса ZBX(jco) и идеального средства измерений (ИСИ), имеющего бесконечно большой импеданс. Составляющая погрешности измерений, обусловленная взаимодействием объекта и СИ, 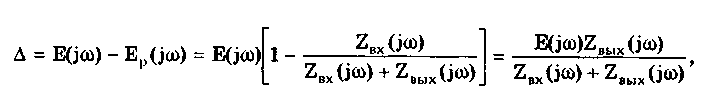 где Ep(j) —ЭДС на входе СИ; Zвых(j) = Z0(j) + Zлс(j) — выходной импеданс объекта измерений, включая линию связи. Зная комплексные величины E(j), ZBX(j), Z0(j) и ZJIC(j), можно рассчитать характеристики и параметры погрешности влияния. 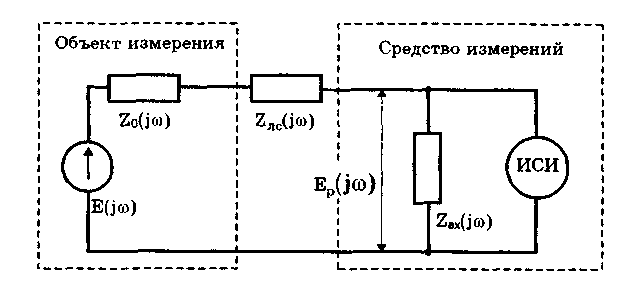 Рис. 12.3. Эквивалентная схема подключения средства измерения к объекту измерения (ИСИ — идеальное средство измерений) Импедансные характеристики электронных СИ нормируются путем представления его входных цепей в виде эквивалентной схемы замещения и задания значений составляющих ее элементов. Некоторые схемы замещения приведены в табл. 12.1 (цифрами 1 и 2 обозначены входные клеммы СИ). 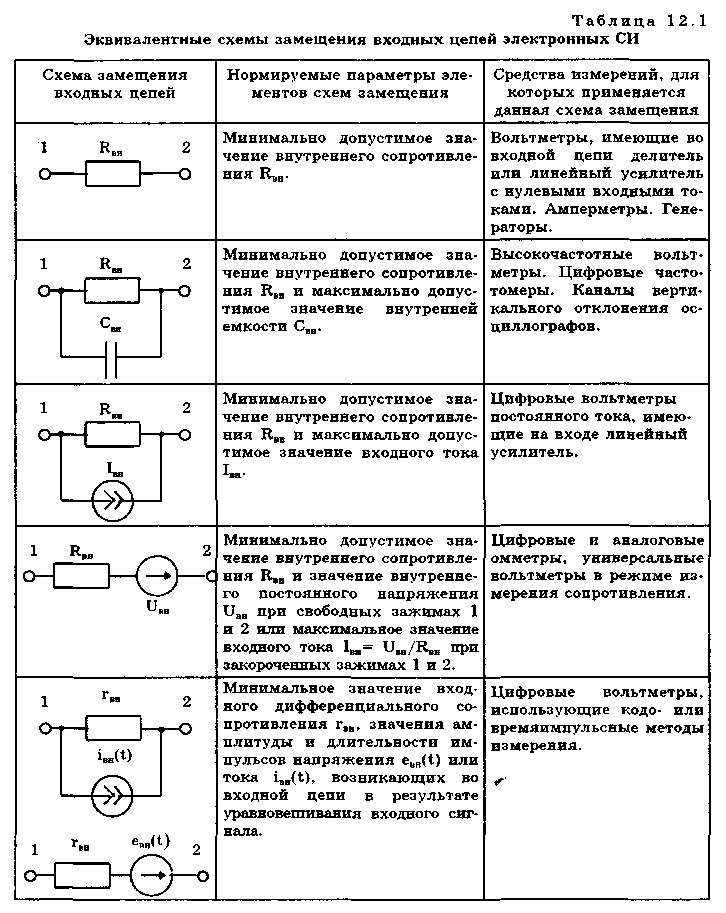 12.7. Комплексы нормируемых метрологическиххарактеристик средств измеренийБольшое разнообразие групп СИ делает невозможной регламентацию конкретных комплексов MX для каждой из этих групп в одном нормативном документе. В то же время все СИ не могут характеризоваться единым комплексом нормируемых MX, даже если он представлен в самой общей форме. Изучение вопроса о рациональной классификации СИ по комплексам нормируемых MX показало [58], что можно выделить ряд общих групп, для которых могут быть назначены общие MX. Основным признаком деления СИ на группы является общность комплекса нормируемых MX, необходимых для определения характерных инструментальных составляющих погрешностей измерений. В этом случае все СИ целесообразно разделить на три большие группы, представленные по степени усложнения MX: 1) меры и цифро-аналоговые преобразователи; 2) измерительные и регистрирующие приборы; 3) аналоговые и аналого-цифровые измерительные преобразователи. При установлении комплекса нормируемых MX принята следующая модель инструментальной составляющей погрешности измерений: lnst = MI*int, где символом « * » обозначено объединение погрешности M1 СИ в реальных условиях его применения и составляющей погрешности int, обусловленной взаимодействием СИ с объектом измерений. Под объединением понимается применение к составляющим некоторого функционала, позволяющего рассчитать погрешность, обусловленную их совместным воздействием. В каждом случае функционал определяется исходя из свойств конкретного СИ. Всю совокупность MX можно разбить на две большие группы. В первой из них инструментальная составляющая погрешности определяется путем статистического объединения отдельных ее составляющих. При этом доверительный интервал, в котором находится инструментальная погрешность, определяется с заданной доверительной вероятностью меньше единицы. Для MX этой группы принята следующая модель погрешности в реальных условиях применения (модель 1): 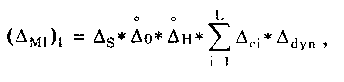 где s — систематическая составляющая; 0 — случайная составляющая; ̊H — случайная составляющая, обусловленная гистерезисом; с1— объединение дополнительных погрешностей; dyn — динамическая погрешность; L — число дополнительных погрешностей, равное всех величин, существенно влияющих на погрешность в реальных условиях. В зависимости от свойств СИ данного типа и рабочих условий его применения отдельные составляющие могут отсутствовать. Первая модель выбирается, если допускается, что погрешность изредка превышает значение, рассчитанное по нормируемым характеристикам. При этом по комплексу MX можно рассчитать точечные и интервальные характеристики, в которых инструментальная составляющая погрешности измерений находится с любой заданной доверительной вероятностью, близкой к единице, но меньше ее. Для второй группы MX статистическое объединение составляющих не применяется. К таким СИ относятся лабораторные средства, а также большинство образцовых средств, при использовании которых не производятся многократные наблюдения с усреднением результатов. Инструментальная погрешность в данном случае определяется как арифметическая сумма наибольших возможных значений ее составляющих. Эта оценка дает доверительный интервал с вероятностью, равной единице, являющийся предельной оценкой сверху искомого интервала погрешности, охватывающего все возможные, в том числе весьма редко реализующиеся, значения. Это приводит к существенному ужесточению требований к MX, что может быть применимо только к наиболее ответственным измерениям, например связанным со здоровьем и жизнью людей, с возможностью катастрофических последствий неверных измерений и т.п. Арифметическое суммирование наибольших возможных значений составляющих инструментальной погрешности приводит к включению в комплекс нормируемых MX пределов допускаемой погрешности, а не статистических моментов. Это допустимо также для СИ, имеющих не более трех составляющих, каждая из которых определяется по отдельной нормируемой MX. В этом случае расчетные оценки инструментальной погрешности, полученные арифметическим объединением наибольших значений ее составляющих и статистическим суммированием характеристик составляющих (при вероятности, хотя и меньшей, но достаточно близкой к единице), практически различаться не будут. Для рассматриваемого случая модель 2 погрешности СИ: 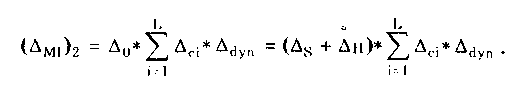 Здесь D0 = Ds + D̊H — основная погрешность СИ без разбиения ее на составляющие (в отличие от модели 1). Модель 2 применима только для тех СИ, у которых случайная составляющая пренебрежимо мала. Вопросы выбора MX достаточно детально регламентированы в ГОСТ 8.009—84, где приведены характеристики, которые должны нормироваться для названных выше групп СИ. Приведенный перечень может корректироваться для конкретного средства измерений с учетом его особенностей и условий эксплуатации. Важно отметить, что не следует нормировать те MX, которые оказывают несущественный по сравнению с другими вклад в инструментальную погрешность. Определение того, важна ли данная погрешность или нет, производится на основе критериев существенности, приведенных в ГОСТ 8.009-84 и подробно проанализированных в [58]. 12.8. Расчет погрешностей средств измеренийпо нормированным метрологическимхарактеристикамРасчет инструментальной погрешности в силу ее случайности сводится к нахождению интервала, в котором она находится с заданной вероятностью Р. Определение интервала осуществляется в три этапа. На первом этапе вычисляются математическое ожидание М[Di] и дисперсия D[Di] каждой из четырех составляющих погрешности. Для основной погрешности вид расчетных формул зависит от того, какие MX нормированы. Если заданы нормированные значения M[D0S] и D[D0S] = 2[D0S] систематической составляющей, то характеристики основной погрешности имеют вид: 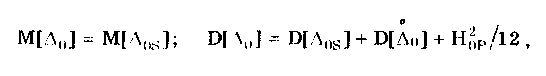 где D[D̊0] = 2[D̊0]. Если нормированы пределы допускаемой систематической погрешности D0SP, то 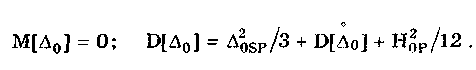 Если же нормированы пределы допускаемой основной погрешности D0р, то в предположении равномерного распределения значений погрешности для совокупности СИ данного типа имеем 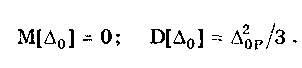 Для определения характеристик дополнительной погрешности необходимо знать не только нормированные функции влияния (), но и статистические характеристики влияющих величин . От того, какие характеристики в реальных условиях применения СИ известны, зависит достоверность получаемых оценок инструментальной составляющей. Если для СИ нормированы функции влияния i(i) каждой влияющей величины i отдельно, то 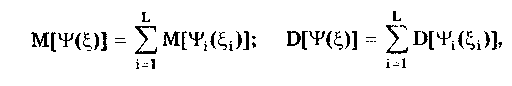 где L — число внешних влияющих величин. Основы методики расчета величин M[i(i)] и D[i(i)] изложены в разд. 12.4. Если же для СИ нормирована функция совместного влияния нескольких величин i(I, 2,…, L), то ее математическое ожидание и дисперсию находят по известным правилам определения статистических характеристик функций нескольких случайных величин. Математическое ожидание и дисперсия динамической погрешности могут быть оценены путем анализа формул, выражающих связь значений погрешностей с параметрами измеряемого сигнала и нормированными динамическими характеристиками СИ. Расчет характеристик динамических погрешностей является одним из самых сложных при определении инструментальной погрешности. Отдельные его аспекты подробно рассмотрены в [6, 56, 58] и руководящем документе РД 50-453-84 "Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета". На втором этапе производится оценка инструментальной погрешности inst, обусловленной взаимодействием СИ с объектом измерений. Она существенным образом зависит от характера этого взаимодействия и вида импедансной характеристики. После определения характеристик всех ее составляющих производится расчет таких же характеристик инструментальной погрешности путем сложения найденных математических ожиданий M[inst] и дисперсий D[inst] соответственно. На третьем этапе производится оценка интервала, в котором с доверительной вероятностью Р находится инструментальная погрешность измерения:  где К — коэффициент, зависящий от вида закона распределения инструментальной погрешности и заданной доверительной вероятности. Его выбор в каждом случае является в большой мере произвольным. Если декларируется нормальный закон распределения результирующей инструментальной погрешности, то велика вероятность неоправданного увеличения интервальной оценки. При выборе равномерного закона возможно уменьшение надежности получаемой оценки. Эти вопросы подробно рассматривались в разд. 9.1 при обсуждении способов получения кван-тильного коэффициента zp. Коэффициент К является не чем иным, как таким же множителем. Его можно рассчитать по формуле К = 5(Р—0,5) при 0,8 < Р <1, определить по графику зависимости К(Р), приведенному в РД 50-453—84, а также в [56, 58]. Следует отметить, что наиболее распространенным является значение коэффициента К = 2, что соответствует доверительной вероятности 0,96. В заключение отметим, что рекомендовать конечное число расчетных формул, применимых при оценке инструментальной погрешности при различных условиях, видах и методиках измерений, не представляется возможным. В каждом конкретном случае необходимо учитывать все существенные влияющие факторы. 12.9. Классы точности средств измеренийХарактеристики, введенные ГОСТ 8.009—84, наиболее полно описывают метрологические свойства СИ. Однако в настоящее время в эксплуатации находится достаточно большое число СИ, метрологические характеристики которых нормированы несколько по-другому, а именно на основе классов точности. Класс точности — это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401-НО. Пределы допускаемой основной погрешности СИ, определяемые классом точности — это интервал, в котором находится значение основной погрешности СИ. Если СИ имеет незначительную случайную составляющую, то определение СИ относится к нахождению систематической погрешности и случайной погрешности, обусловленной гистерезисом, и является достаточно строгим. При этом предел DСИ = D0SP + 0,5НОР. Если СИ имеет существенную случайную погрешность, то для него определение предела допускаемой основной погрешности является нечетким. Его следует понимать как интервал, в котором находится значение основной погрешности с неизвестной вероятностью, близкой к единице: DСИ = ±(D0SP + K[D̊0] + 0,5H0P) где К — коэффициент, зависящий от доверительной вероятности Р. Предел допускаемой дополнительной погрешности, вызванной изменением влияющей величины , может оыть найден с использованием функции влияния Y(x): DДСИ = [dY(x)/d]max. B частности, если Y(x) = A, то DДСИ = . Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерений может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величиям ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины. Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ. Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: = ±а или = ± (а + bх), где х — значение измеряемой величины или число делений, отсчитанное по шкале; a, b — положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность (рис.12.4,а), а вторая — сумму аддитивной и мультипликативной погрешностей (рис.12.4,в). В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, "Класс точности М", а на приборе — буквой "М". Для обозначения используются прописные буквы латинского алфавита или римские цифры, причем меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. 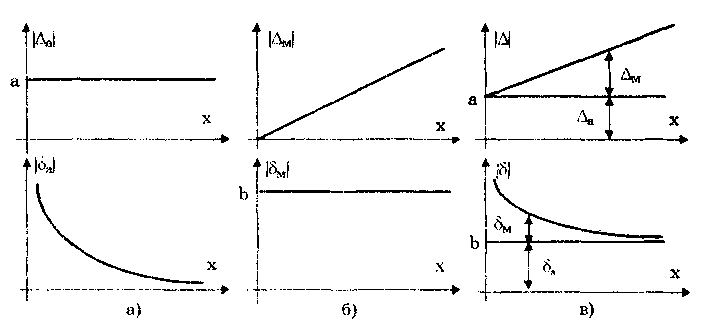 Рис. 12.4. Аддитивная (а), мультипликативная (б) и суммарная (в) погрешности в абсолютной и относительной формах Пределы допускаемой приведенной основной погрешности определяются по формуле =/xN = ±р, где xn — нормирующее значение, выраженное в тех же единицах, что и ; р — отвлеченное положительное число, выбираемое из ряда значений: (1; 1,5; 2; 2,5; 4; 5; 6)10n; n=1; 0; -1; -2;... Нормирующее значение xn устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалами и для измерительных преобразователей, если нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, хы равно модулю разности пределов измерений. Например, для вольтметра термоэлектрического термометра с пределами измерений 100 и 600°С нормирующее значение равно 500°С. Для СИ с заданным номинальным значением xn устанавливают равным этому значению. Для приборов с существенно неравномерной шкалой xn принимают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка определяются по формуле = /х = ±q , если = а. Значение постоянного числа q устанавливается так же, как и значение числа р. Класс точности на прибор обозначается в виде В случае, если абсолютная погрешность задается формулой (а + bх), пределы допускаемой относительной основной погрешности 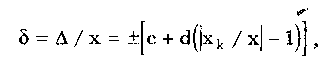 (12.4) (12.4)где с, d — отвлеченные положительные числа, выбираемые из ряда: (1; 1,5; 2; 2,5; 4; 5; 6)10n; п=1; 0; -1; -2и т.д.; xk — больший (по модулю) из пределов измерений. При использовании формулы (12.4) класс точности обозначается в виде "0,02/0,01", где числитель — конкретное значение числа с, знаменатель — числа d. В обоснованных случаях пределы допускаемой относительной основной погрешности определяют по более сложным формулам либо в виде графика или таблицы. В стандартах или технических условиях на СИ указывается минимальное значение Х0 , начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения. Предел допускаемой дополнительной погрешности дси может указываться в виде: • постоянного значения для всей рабочей области влияющей величины или постоянных значений по интервалам рабочей области влияющей величины; • отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу; • зависимости предела дcи от влияющей величины (предельной функции влияния); • функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния. Пример 12.3. Отсчет по равномерной шкале прибора с нулевой отметкой и предельным значением 50 А составил 25 А. Пренебрегая другими видами погрешностей, оценить пределы допускаемой абсолютной погрешности этого отсчета при условии, что класс точности прибора равен: 0,02/0,01; 1. Для прибора с классом точности 0,02/0,01, согласно формуле (12.4), при х = 25 A, xk = 50 А, с = 0,02, d = 0,01 (учитывая, что относительная погрешность выражается в процентах) получим 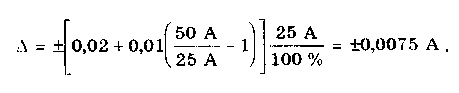 2. Для прибора класса точности 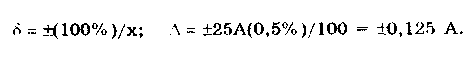 3. Для прибора класса точности 0,5, учитывая, что нормирующее значение xn равно пределу измерения 50 А, .получаем: = ±(100% )/хN; = ±50А(0,5% )/100 = ± 0,25 А. Контрольные вопросы, 1. Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений. 2. Какой нормативный документ регламентирует нормирование метрологических характеристик средств измерений? 3. На какие группы делятся нормируемые метрологические характеристики? 4. Какие метрологические характеристики относятся к характеристикам, предназначенным для определения результатов измерений? 5. Какие метрологические характеристики описывают погрешность средств измерений? Каким образом производится их нормирование? 6. Какая математическая модель используется для описания инструментальной составляющей погрешности измерения? 7. Какие метрологические характеристики описывают чувствительность средств измерений к влияющим величинам? 8. Как осуществляется нормирование динамических характеристик средств измерений? 9. Какие метрологические характеристики относятся к импедансным характеристикам средств измерений? 10. Что такое комплексы нормируемых метрологических характеристик? 11. Что такое классы точности средств измерений? 12. Какие различные способы выражения класса точности существуют? |
