Исправленная контрольная по ОТМО. В. Г. Карташевский Основы теории массового обслуживания
 Скачать 1.49 Mb.
|
Потоки бывают однородными и неоднородными (просто самолёты или самолёты по маркам). Обычно используют однородные потоки.Регулярный поток – события следуют одно за другим через строго определенные промежутки времени.  Рис.1.2. Поток событий при независимых  Рассмотрим поток событий, представленный на рис.1.2, где Т1, Т2… - случайные интервалы времени (случайные величины), независимые между собой. Такой поток называется потоком Пальма или потоком с ограниченным после-действием. Поток называется ординарным, если для малого Δt выполняется условие:  , (1.1)где  - вероятность того, что за Δtпроизойдёт одно собы-тие и  - вероятность того, что за Δt произойдёт более одного события.Таким образом, поток можно считать ординарным, если за малый промежуток времени может произойти не более одного события (или ни одного события, вероятность чего обозначим  ).Для любого Δtочевидно справедливо:  , (1.2)т.к. составляющие формулы (1.2) определяют полную группу несовместных событий. Для ординарного потока:  , (1.3) потому что  , где  - величина, порядок малос-ти которой выше чем Δt, т. е.: . (1.4)В качестве примера ординарного потока можно привести ситуацию на автостраде, когда машины пересекают линию «Стоп», даже при многорядном движении. Пример неординарного потока – поток пассажиров, прибывающих в лифте на данный этаж. Стационарный поток определяется следующим образом. Для стационарного потока вероятность появления некоторого числа событий за интервал τ, зависит только от τ (длины интервала) и не зависит от расположения τ на оси t. Регулярный поток и поток Пальма с одинаково распределёнными интервалами Ti являются стационарными потоками. Возьмём ординарный поток. Среднее число событий, произошедших за время Δt (вычисляется по формуле математического ожидания):  .Если существует предел  , (1.5) то  называется интенсивностью ординарного потока (раз-мерность [1/t]). Для стационарного потока:  - число со-бытий в единицу времени.
Пусть дан стационарный поток Пальма (см. рис.1.3). Все случайные интервалы времени между событиями независимы и имеют одинаковую функцию распределения F(t), которой соответствует плотность вероятности w(t). Здесь в соответствии с принятыми в теории вероятностей правилами записи формул, если случайная величина обозначена большой буквой Т, то аргумент плотности вероятности этой случайной величины обозначается малой буквой t. Это не должно приводить к путанице в обозначениях и ни в коем случае не означает, что w(t) рассматривается как функция текущего времени. На ось времени случайным образом «падает» точка S, и её положение никак не связано с моментами появления событий. Требуется найти закон распределения того участка T*, на который упала точка (см. рис.1.3). Описанная модельная ситуация возникает, когда пассажир (точка S) приходит на остановку, а автобус уже ушёл (предполагается, что поток автобусов – стационарный поток Пальма).  Рис.1.3. Интервал времени, на который падает точка. Закон распределения  интервалаT*, когда пассажир стоит на остановке, отличается от F(t). Упрощенное объяснение этого факта можно представить следующим образом (см. рис.1.4). Рис.1.4. К определению закона распределения ПустьT принимает два значения с вероятностью 0,5: t1=0,8 и t2=0,2. На остановку приходит пассажир. Более вероятно, что он попадёт на участок длины 0,8. Хотя в среднем число интервалов t1 и t2 одинаково, но t1 в четыре раза длиннее t2. Поэтому вероятность попадания в отрезок длиной 0,8 в четыре раза больше вероятности попадания в отрезок 0,2. Получается, что эти вероятности равны соответственно 0,8 и 0,2. Итак, закон распределения, на который упала точка, отличается от априорного. Найдём в общем виде плотность w*(t) того интервалаT*, на который случайным образом упала точка. Возьмём интервал (t, t+dt). Тогда:  - вероятность того, что S попадёт на интервал, длина которого заключена в промежутке (t,t+dt). Эту вероятность можно определить как отношение суммарной длины таких промежутков на очень большом интервале к длине этого большого интервала. Пусть общее число промежутков (больших и маленьких) на большом интервале равно N. Среднее число промежутков, длина которых лежит в интервале (t, t+dt), по закону больших чисел равно  , где  - вероятность наличия любого интервала длиной из промежутка (t,t+dt) среди всехN интервалов. Средняя длина такого интервала -  . Средняя суммарная длина таких промежутков -  . Средняя общая длина большого интервала -  , где  - символ усреднения. При известной плотности w(t) среднее Е{T} записывается в виде . (1.6)(  - еще одно обозначение среднего).Следовательно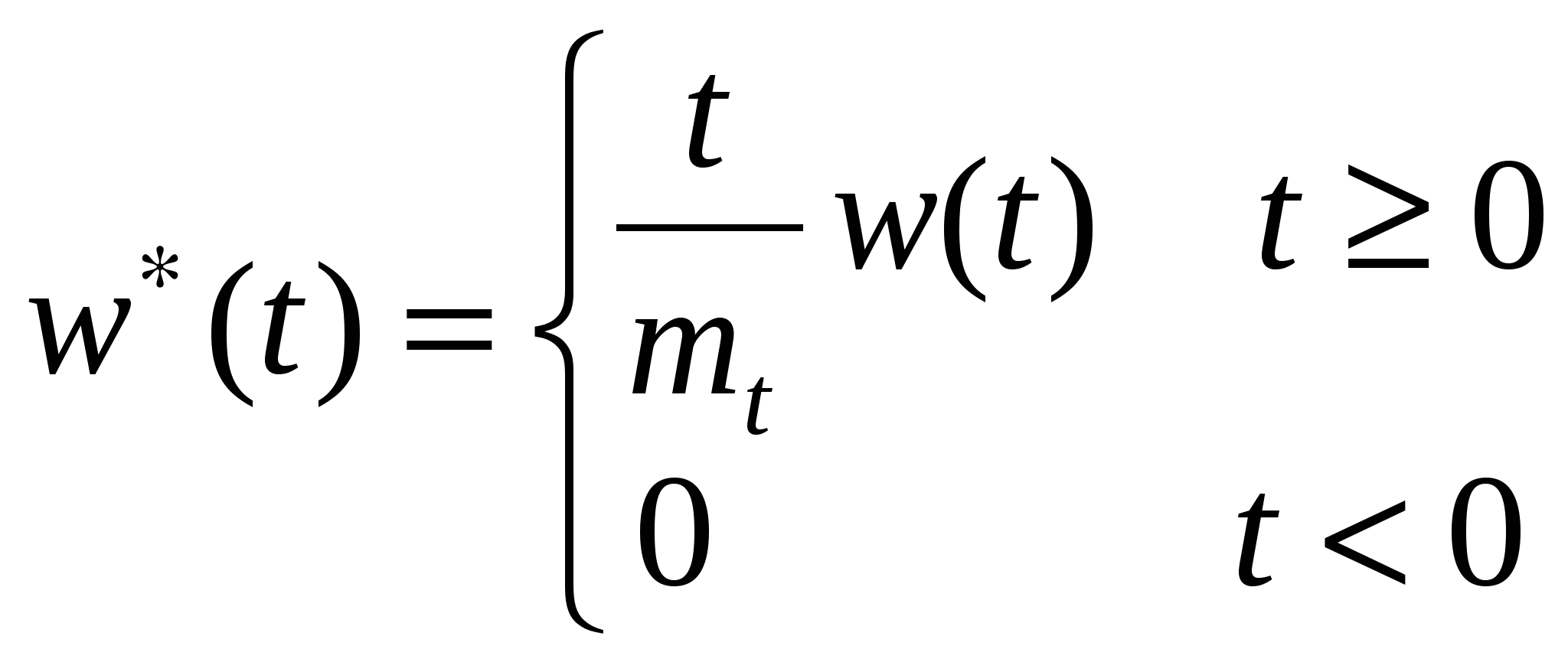:  . (1.7)При  : . (1.8)Как следует из (1.8)  обладает всеми свойствами плотности вероятности. Чтобы найти среднее и дисперсию случайной величины T* целесообразно использовать аппарат характеристических функций. По определению характеристическая функция g(x)определяется как:  (1.9) и представляет собой прямое преобразование Фурье плотности вероятности. Характеристическая функция безразмерна, а перемен-ная x имеет размерность обратную размерности случайной величины T. Соответственно плотность вероятности по известной характеристической функции может быть найдена с помощью обратного преобразования Фурье  . (1.10)Свойства характеристической функции:
Если все Ti распределены одинаково, то 
 , , (1.11) . (1.12)Поэтому  , (1.13) , (1.14)где  - дисперсия (второй центральный момент) случайной величины Т. Заметим здесь, что через производные более высокого порядка от характеристической функции можно соответственно найти моменты распределения случайной величины более высоких порядков.4) Если случайная величинаT имеет характе-ристическую функцию  , то случайная величина  имеет характеристическую функцию в виде  . (1.15)Найдём характеристическую функцию случайной величины T* - интервала, на который случайным образом упала точка S.  Заметим справедливость соотношения  , с учетом которого можно записать .С использованием выражения (1.13) (  ) для характеристической функции случайной величиныT* окончательно получим . (1.16)На основе выражений (1.16), (1.13) и (1.14) найдём числовые характеристики случайной величины T*. Среднее значение 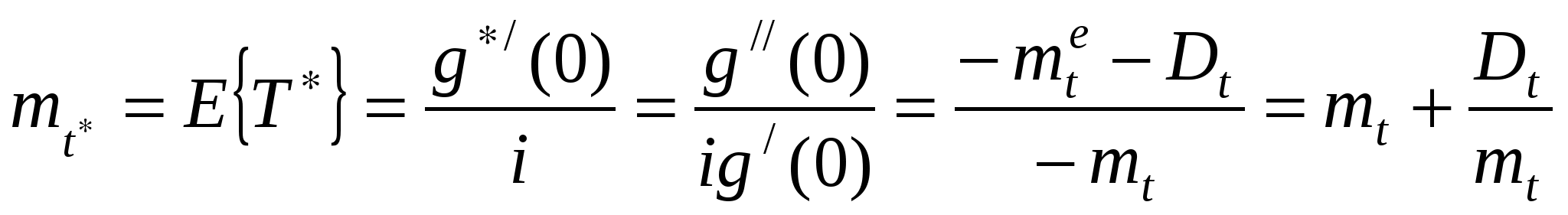 . (1.17)Из (1.17) следует, что всегда  . Лишь в случае регулярного потока событий, когда интервалы становятся неслучайными и, следовательно, Dt=0, получается  . Таким образом, указание на то, что S попало на какой-то интервал, как бы увеличивает его среднюю длину по сравнению с тем, как его оценивали бы без этого указания.Найдём дисперсию случайной величины T*: 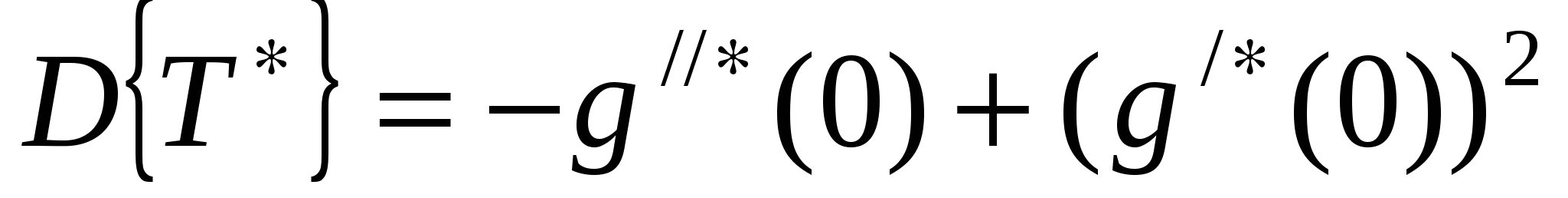 ,  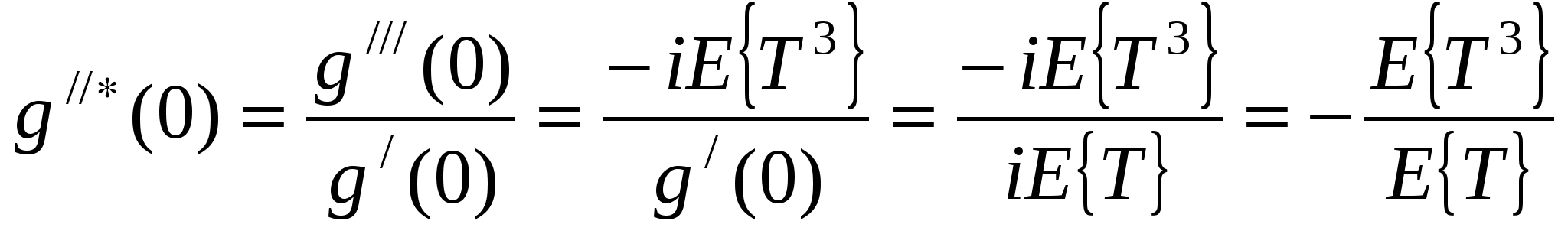, ,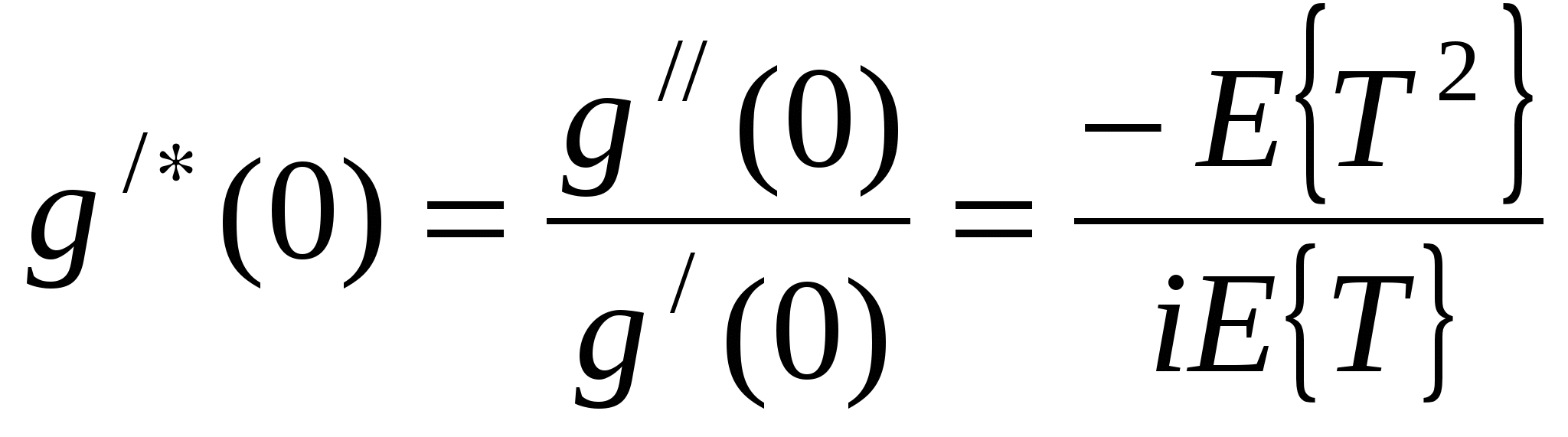 , 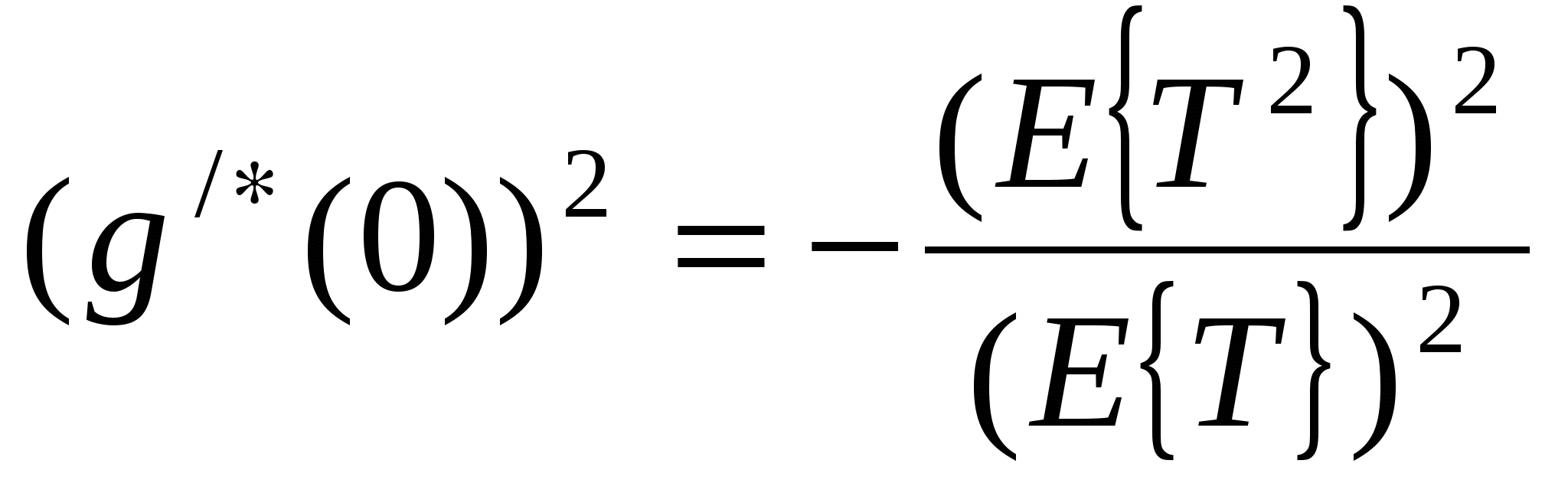. (1.18)Из (1.18) видно, что дисперсия  может быть и больше и меньше дисперсии  .1.3. Закон распределения времени до наступления очередного события |
, то 
.