Исправленная контрольная по ОТМО. В. Г. Карташевский Основы теории массового обслуживания

• Название: В. Г. Карташевский Основы теории массового обслуживания
• Анкор: Исправленная контрольная по ОТМО.doc
• Дата: 28.12.2017
• Размер: 1.49 Mb.
• Имя файла: Исправленная контрольная по ОТМО.doc
• Тип: Анализ; #13381
• страница: 3 из 4

Пусть имеется стационарный поток Пальма и точка S, занимающая на оси t любое положение (см. рис.1.5).

Рис.1.5. К определению закона распределения .

Плотность распределения интервала T* отличается от плотности распределения всех остальных T и согласно (1.8) записывается в виде . Найдем закон распределения случайной величины .

Для этого рассмотрим гипотезу: интервал T* принял значение на участке (t* , t* + dt^*).

Вероятность справедливости этой гипотезы запишется как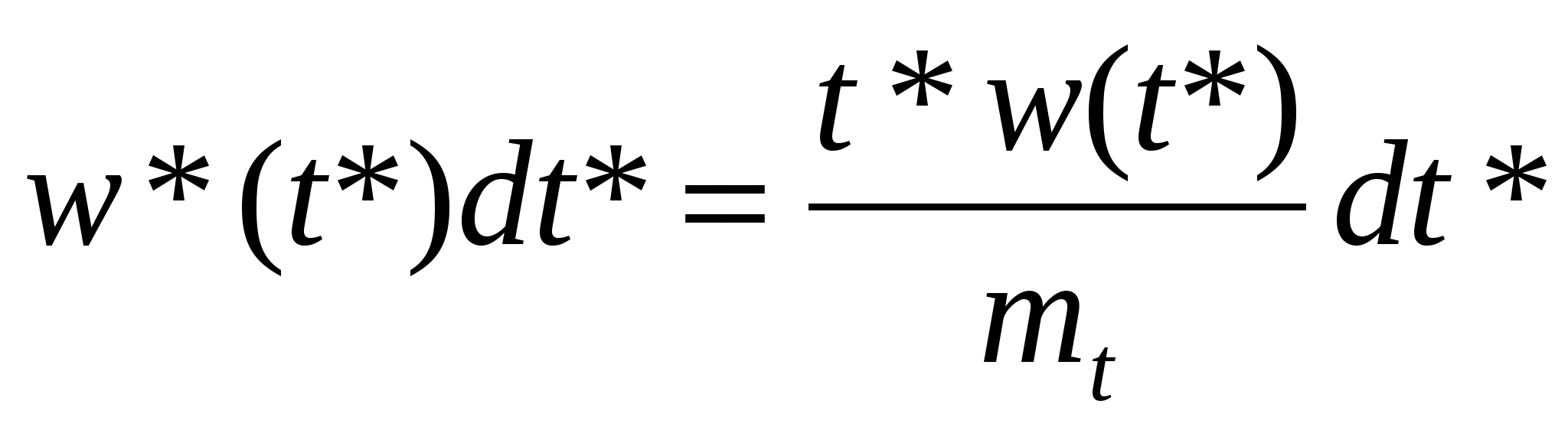

.

Будем искать плотность распределения  при условии справедливости сформулированной гипотезы. Эту условную плотность обозначим .

Нет оснований считать какой-то участок интервалаt*, на который упала точка S, более вероятным для положения этой точки, чем другой. Поэтому точка S на интервалеt* будет распределена равномерно и условная плотность 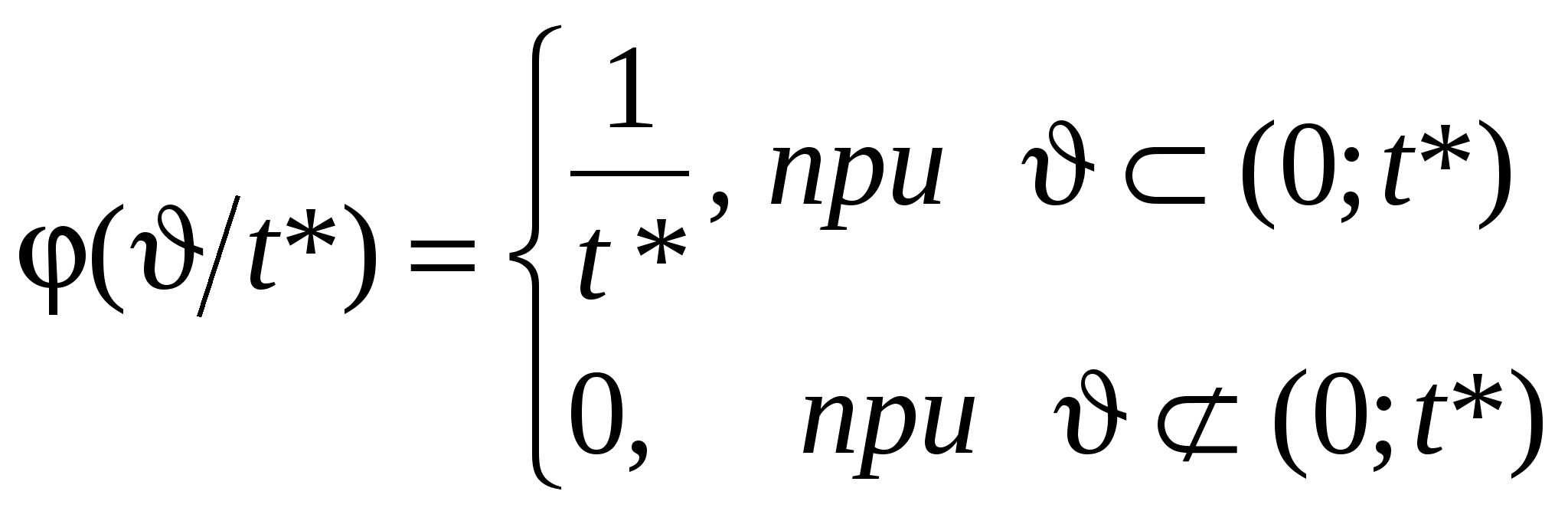тоже будет равномерна

. (1.19)

Совместная плотность  и T* имеет вид:

. (1.20)

Безусловная плотность:

. (1.21)

С учетом (1.19) подынтегральная функция отлична от нуля при 0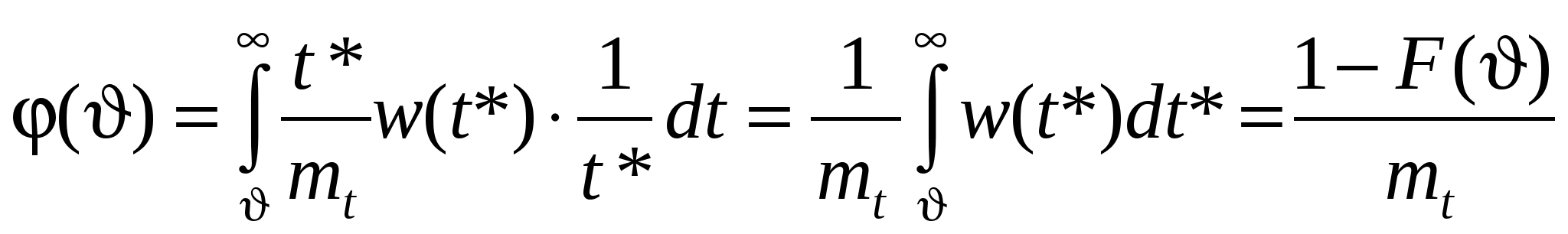  t* , т.е. при t*. Поэтому (1.21) преобразуется к виду

, (1.22)

где F(x) - функция распределения случайной величины T.

Итак: 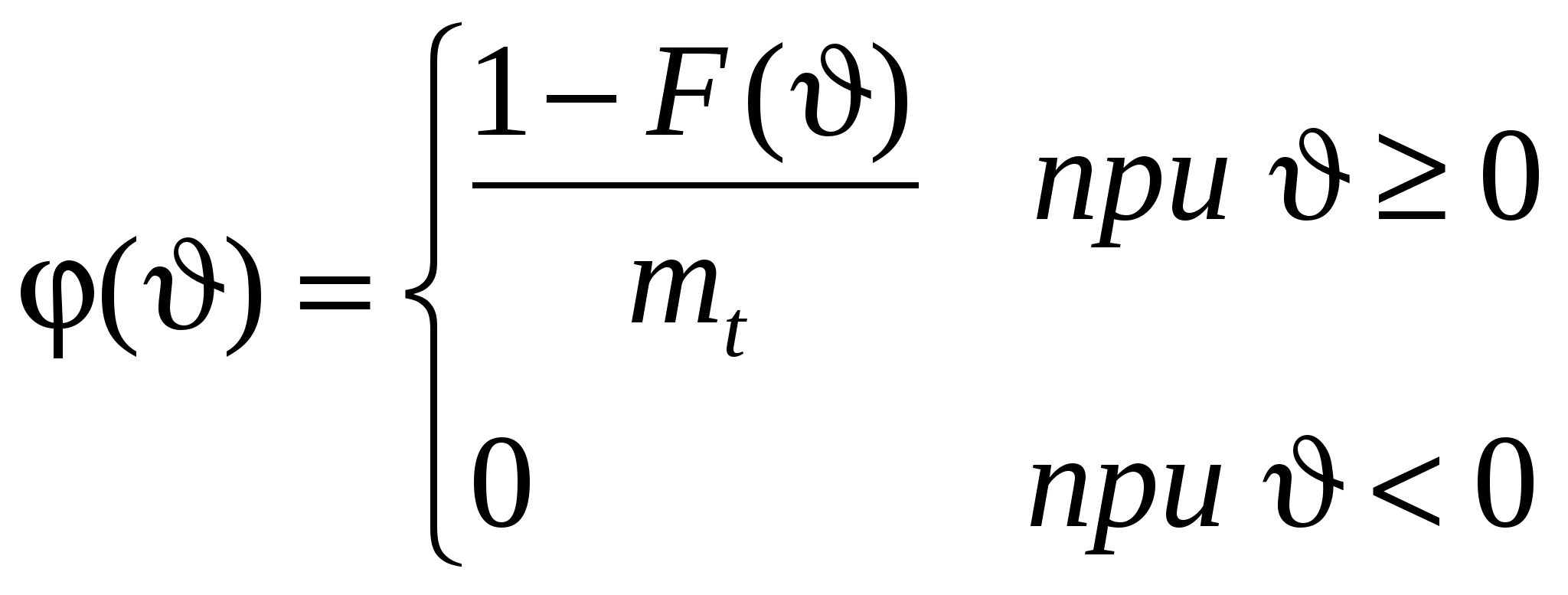. (1.23)

Здесь - математическое ожидание случайной величины T.

Найдем числовые характеристики случайной величины  через её характеристическую функцию

. (1.24)

Интеграл в (1.24) можно вычислить по частям. Обозначая

, ,

имеем , .

Теперь

,

где g(x) – характеристическая функция случайной величины T (как преобразование Фурье w(t)).

Напомним, что согласно (1.11) , ,

поэтому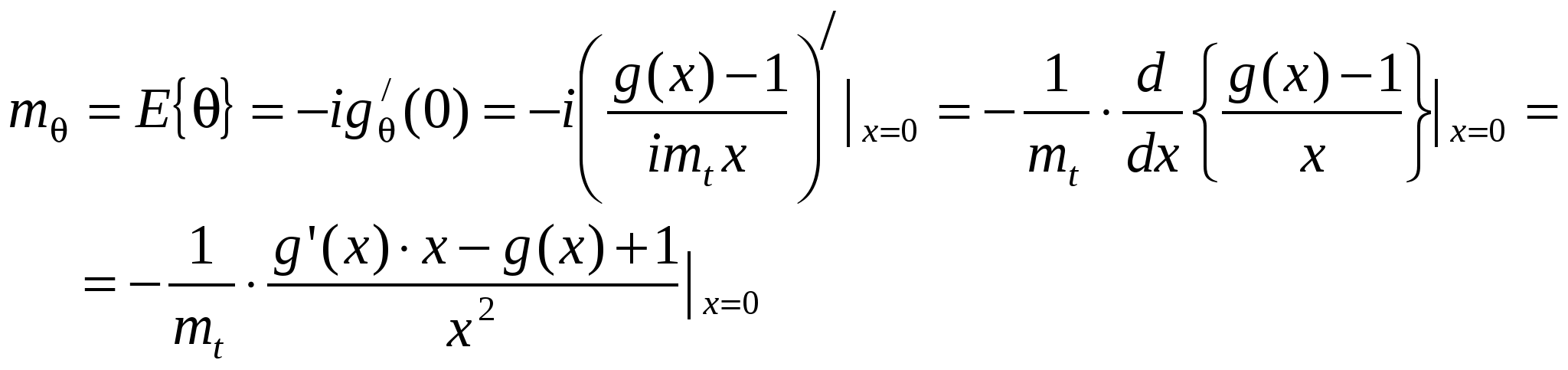: . (1.25)

Найдем и .

.

Если в последнем выражении подставить , то получится неопределенность типа . Раскроем её по правилу Лопиталя. .

Согласно формуле (1.14)

,

поэтому 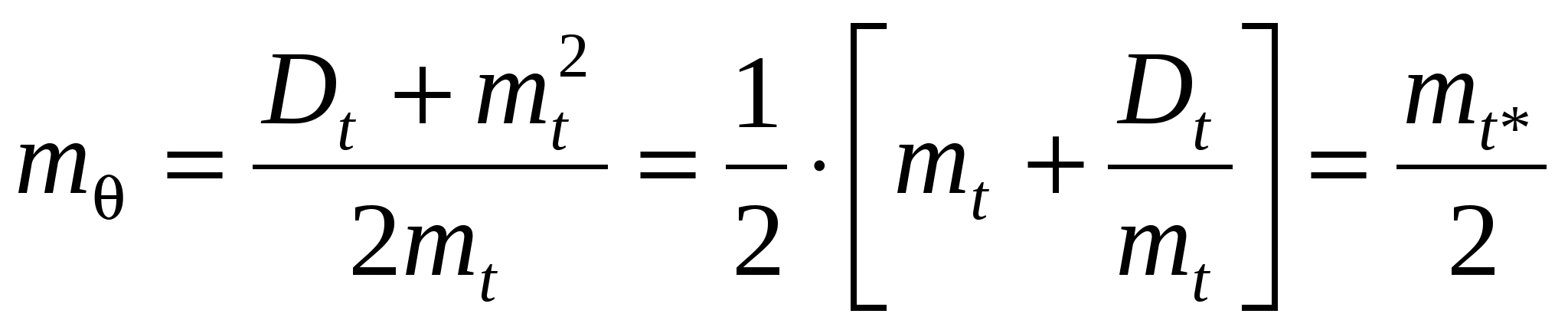(1.26)

(после третьего знака равенства учтена формула (1.17)).

Следовательно, математическое ожидание остатка всегда не меньше, чем половина математического ожидания любого интервала между событиями в стационарном потоке Пальма.

Поступая аналогично, найдем дисперсию

. (1.27)

В заключение параграфа заметим, что случайные величиныН и  зависимы (вследствие соотношения , см. рис.1.5), а закон распределения Нтакой же, как у .

1.4. Пуассоновский поток событий.

Пуассоновский поток – это поток обладающий двумя свойствами – ординарностью и отсутствием последействия.

Понятие ординарности было объяснено выше, а свойство отсутствия последействия можно сформулировать следующим образом: для двух неперекрывающихся интервалов времени число событий, попадающих в один интервал, не зависит от того, сколько событий попало в другой.

Пусть дан стационарный поток с интенсивностью . Из ординарности потока следует:

- вероятность наступления одного события за время :

- вероятность ненаступления события

Рассмотрим интервал , представленный на рис. 1.6. Из независимости (отсутствия последействия) событий на соседних интервалах следует, что вероятность наступления k событий наm интервалах определяется биномиальной формулой:

, (1.28)

где число сочетаний .



Рис. 1.6. К определению пуассоновского потока событий.

Для вычисления факториалов используем формулу Стирлинга

(1.29)

(при m=1 ошибка вычислений по (1.29) составляет 8%, при m=100 ошибка - 0,08%), а для вычисления при

- второй замечательный предел .

С учетом сделанных замечаний формула (1.28) преобразуется к виду

, (1.30) и именно в таком виде она известна как распределение Пуассона, где k=0,1,2,... Вид этого дискретного распределения приведен на рис.1.7.



Рис.1.7. Распределение Пуассона

Заметим, что распределение Пуассона удовлетворяет ус-ловию нормировки .

В случае нестационарного потока распределение Пуассо-на записывается в виде:

, (1.31)

где -среднее число событий, наступающих на интервале T, примыкающем к моментуt,

,

а - интенсивность нестационарного потока.

В стационарном случае и получа-ется формула (1.30).

Найдем среднее и дисперсию распределения Пуассона. Среднее:

. (1.32)

Вычисление (1.32) иллюстрируется следующими соотношения-ми (с учетом условия нормировки)

.

Дисперсия:

. (1.33)

Здесь необходимо отметить, что распределение Пуассона обладает уникальным свойством – равенством среднего и дисперсии, - что отличает его от всех известных распределений и может служить признаком при идентификации распределения на практике. Из отношения



следует, что при больших распределение тесно группиру-ется около среднего. Оценкой  может служить величина , где n- измеренное на практике число событий на интервале Т.

Стационарный пуассоновский поток событий называет-ся простейшим потоком.

Рассмотрим теперь интервалы времени  (см. рис.1.8) между событиями в стационарном пуассоновском потоке, которые представляют собой непрерывные случайные величины.

Возьмем начальный интервал времени (он ничем не отличается от всех остальных), и отметим после 0 некоторую точку x. На интервале (0, x) не будет ни одного события, если .



Рис.1.8. Анализ интервалов времени в пуассоновском потоке

Вероятность выполнения этого неравенства может быть вычислена по формуле (1.30) для с учетом того, что х=Т

.

Далее:

Последнее выражение - это (по определению) функция распределения случайной величины  , т.е. . Но тогда

, (1.34)

т.е. для пуассоновского потока  имеет экспоненциальное расп-ределение для (см. рис. 1.9).



Рис.1.9. Экспоненциальное распределение.

Характеристики экспоненциального распределения:

среднее - ,

дисперсия - .

Если случайная точка S попадает на интервал между событиями в пуассоновском потоке (см. предыдущий параграф), то

. (1.35)

Формула (1.35) – это распределение Эрланга 1-го порядка. При этом согласно формулам (1.17), (1.18) получим

и .

Сравнивая и , а так же и , можно утверж-дать, что наличие случайной точки S в каком-либо интервале пуассоновского потока “раздвигает” его, увеличивая среднее и дисперсию вдвое.

Теперь найдем 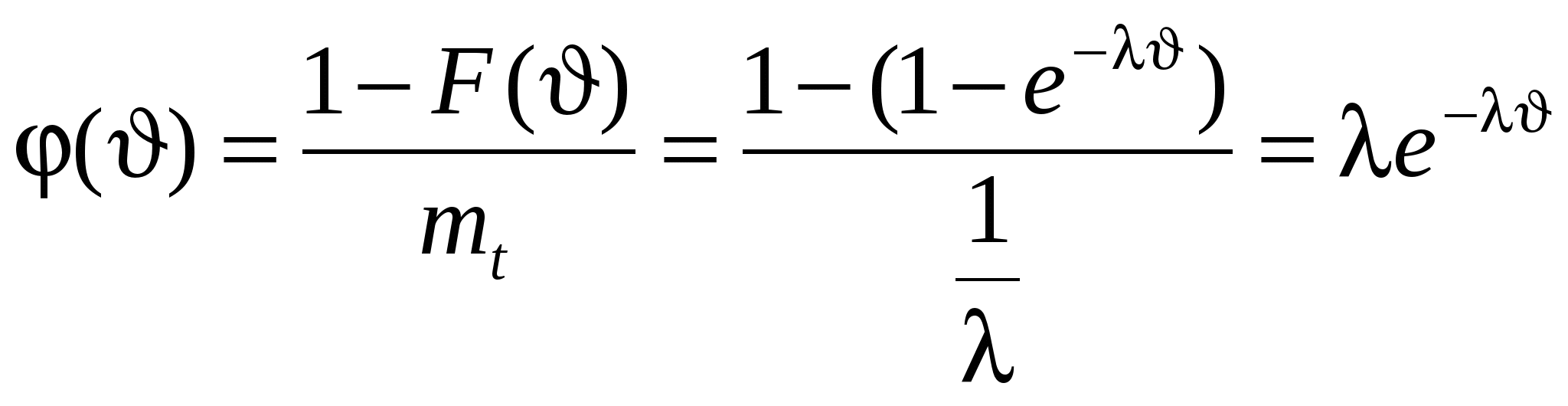для пуассоновского потока.

, (1.36)

что совпадает с экспоненциальным распределением, спра-ведливым для интервала времени между событиями в пуассоновском потоке, т.е. случайная величина  распределена так же, как и T. Это является формой проявления свойства отсутствия последействия. Любая информация о том, как вел себя поток до точки S, не дает нам сведений о том, что произойдет после точки S.

Вычислим характеристическую функцию интервала между соседними событиями в простейшем потоке.

. (1.37)

Итак, поток Пальма является простейшим, если характеристическая функция интервала между соседними событиями равна .

В заключение отметим одно важное свойство пуассоновского процесса. Пусть есть m пуассоновских потоков с интенсивностями 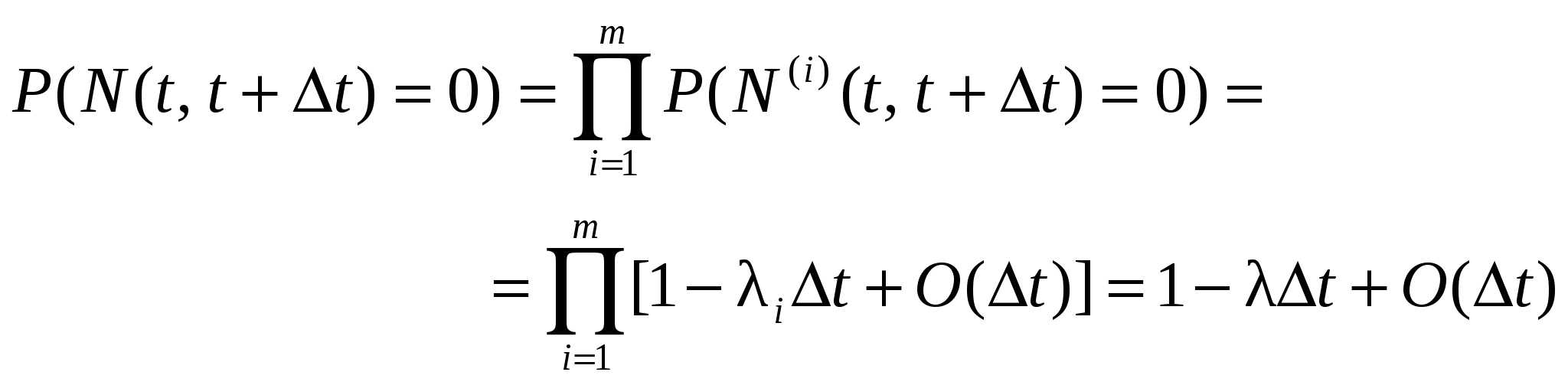,, … . Объединим эти потоки. Тогда объединенный поток будет опять пуассоновский с интенсивностью . Покажем справедливость этого утверждения.

Пусть - число событий i-го процесса в промежутке ,i=1,2…m. - число событий в объединенном процессе.

,

где . Ответ становится очевидным, если учесть, что в степени выше первой является величиной высшего порядка малости по сравнению с .

Аналогично: .

1.5. Вывод формулы Пуассона через производящую функцию.

Рассмотрим поток событий, обладающий свойствами ординарности и отсутствия последействия. Пусть - веро-ятность того, что за малый интервал времени , примы-кающий к моменту времени t, произойдет n событий. Очевидно , и будем считать, что выполняется условие нормировки . Опишем динамику изменения вероят-ности состояния потока за время . Дляn=0 (отсутствие событий на интервале ) можно записать:

. (1.38а)

Множитель является в силу ординарности потока вероятностью того, что за интервал не произойдет ни одного события. Для любого согласно формуле полной вероятности аналогично (1.38а) запишем

. (1.38б)

Из последнего выражения легко получить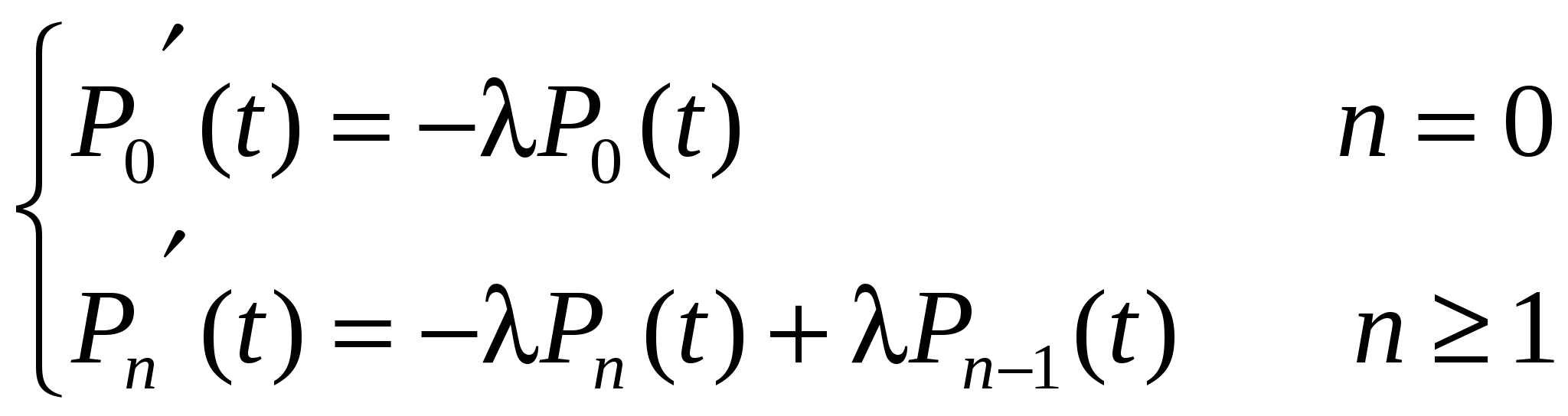

для n1.

При слева получается производная , и в соответствие с этим выражения (1.38а) и (1.38б) можно переписать в дифференциальной форме.

. (1.39)

Это - дифференциально-разностные уравнения, которые удоб-но решать, используя производящую функцию. По определению производящая функция является Z – преобразованием распре-деления вероятностей и записывается в виде:

, (1.40)

гдеz – любое комплексное число, котороедает сходимость сум-мы в (1.40).

Из (1.40) следует, что если продифференцировать nраз по z, то можно найти , положив z=0, т.е.

. (1.41)

При решении уравнений начало отсчета времени можно выбирать произвольно, даже после того, как произойдет некоторое число событий. Возможно, что при t=0 уже произошлоi событий. Тогда:

при ,

при .

Таким образом

. (1.42)

Из определения также следует:

, (1.43)

и . (1.44)

Умножим систему (1.39) на (первое уравнение на ) и про-суммируем по n, тогда получим:

.

Слева от знака равенства согласно (1.44) записана производная . Первое слагаемое справа очевидно имеет вид , а второе представляется как

.

В итоге получаем дифференциальное уравнение

,

которое, как известно, имеет решение:

.

Константа C определяется из начальных условий. Пусть при t=0 не было ни одного события. Тогда из (1.42) следует, что т.к. i=0. Поэтому С=1. Окончательно получаем:

. (1.45)

Теперь воспользуемся формулой (1.41) :

,

,



.

Последняя формула совпадает с распределением Пуассона, гдеt интерпретируется как интервал (0,t).