Исправленная контрольная по ОТМО. В. Г. Карташевский Основы теории массового обслуживания
 Скачать 1.49 Mb.
|
|
1.6 Другие стационарные потоки Пальма. Регулярный поток: Здесь  , что и обозначено на рис.1.10. Из теории вероятностей известно, что плотность вероятности неслучайной величины определяется дельта-функцией. Рис.1.10. Регулярный поток. Поэтому для постоянного интервала  можно записать . (1.46)Напомним здесь основные свойства дельта-функции. 1. Фильтрующее свойство. Если  - произвольная функция (без разрывов в 0), то справедливо соотношение  . Здесь – малая константа. 2. При   . Естественно, что и в бесконечных пределах интегрирования результат будет такой же. Это позволяет утверждать, что дельта-функция как плотность вероятности удовлетворяет условию нормировки.3.  при  .4.  .Вернемся к регулярному потоку. Для него очевидно  . Найдём плотность вероятности интервала, на который падает точка S . (1.47)Как видно из (1.47) случайная точка S никак не изменяет вероятностные свойства интервала, на который она попадает. Найдём закон распределения времени от случайной точки до очередного события 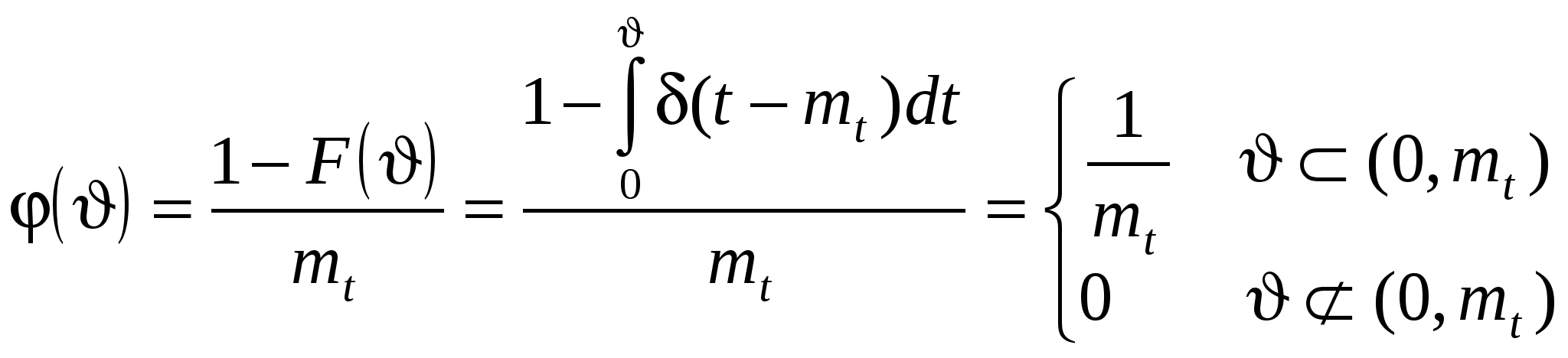 . (1.48)Получился равномерный закон для плотности вероятности. В этом нет ничего удивительного, если вспомнить, что при падении точки S было предположено, что она с равной вероятностью может попасть в любой бесконечно малый промежуток интервала Т*. Найдём числовые характеристики распределения (1.48). Из формулы (1.26)  . Из формулы (1.27) 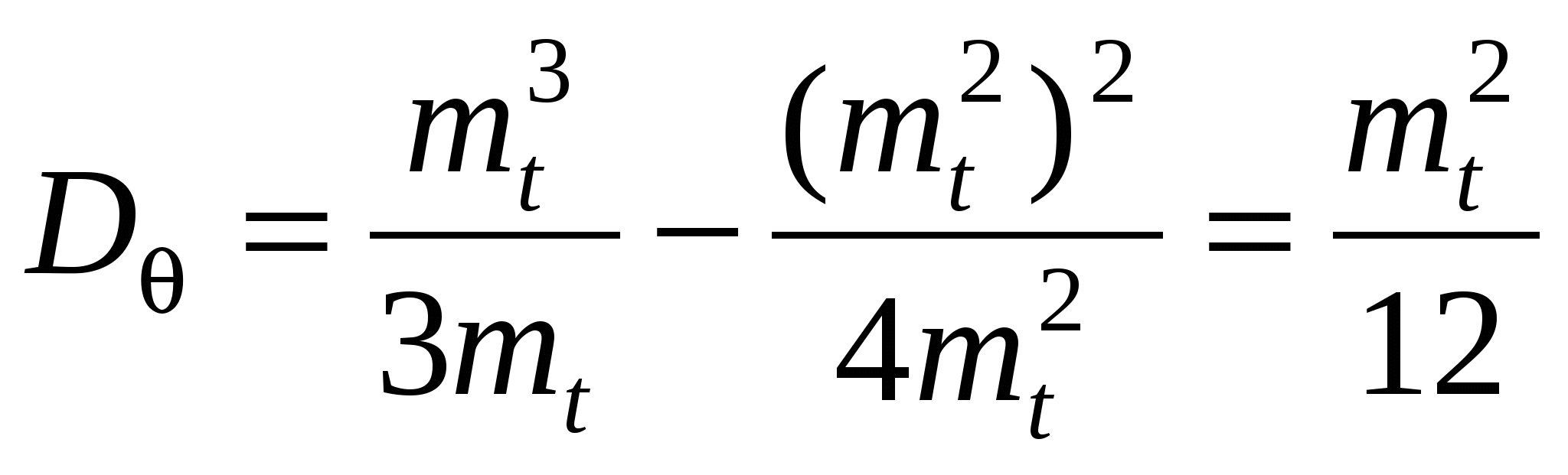 . Характеристическая функция:  . (1.49)Регулярный поток для моделирования потока событий используется редко, так как он обладает неограниченным последействием, т.е., зная лишь один момент наступления события в регулярном потоке, можно восстановить всё прошлое и предсказать всё будущее потока. Нормальный поток. По определению одномерная нормальная плотность вероятности имеет вид (формула записана применительно к случайной величине Т ): 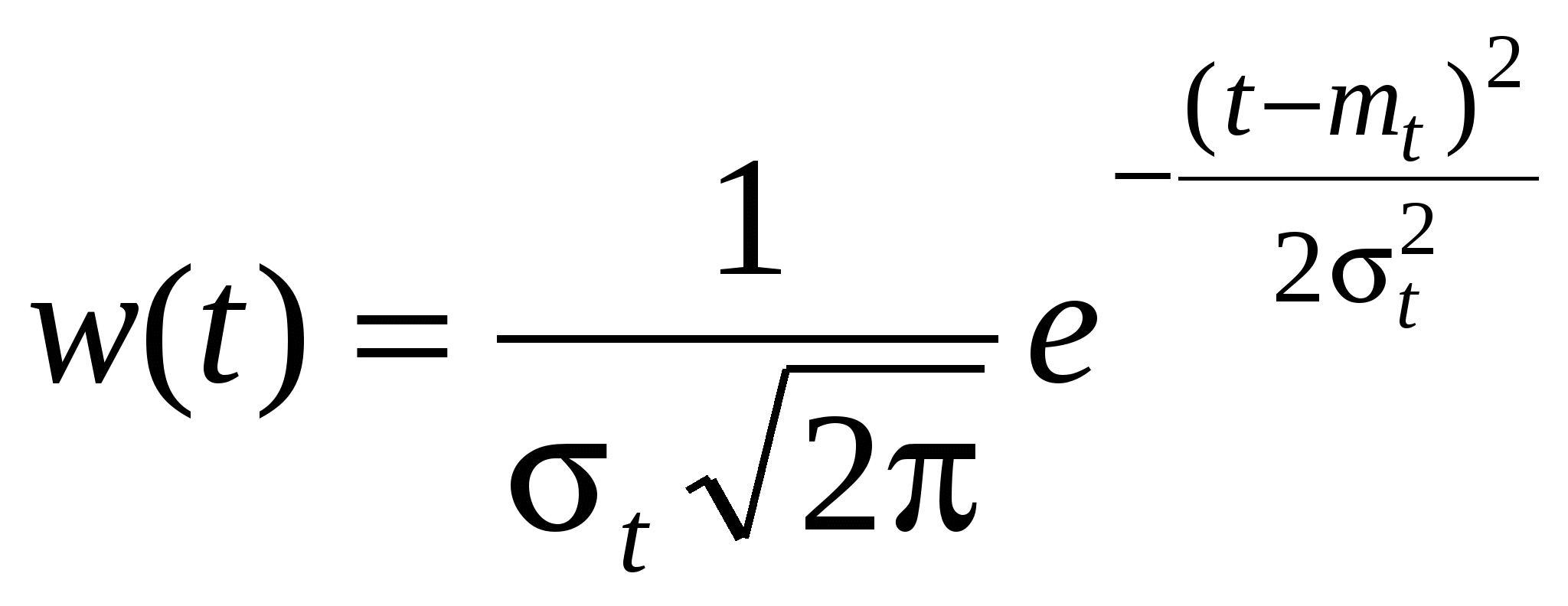 . (1.50)В (1.50) - среднее значение и  - дисперсия распределения. График нормальной плотности приведен на рис.1.11. Рис.1.11. График нормальной плотности вероятности. Строго говоря, интервал времени не может быть распределён по нормальному закону, так как область определения нормального закона  . Однако, ес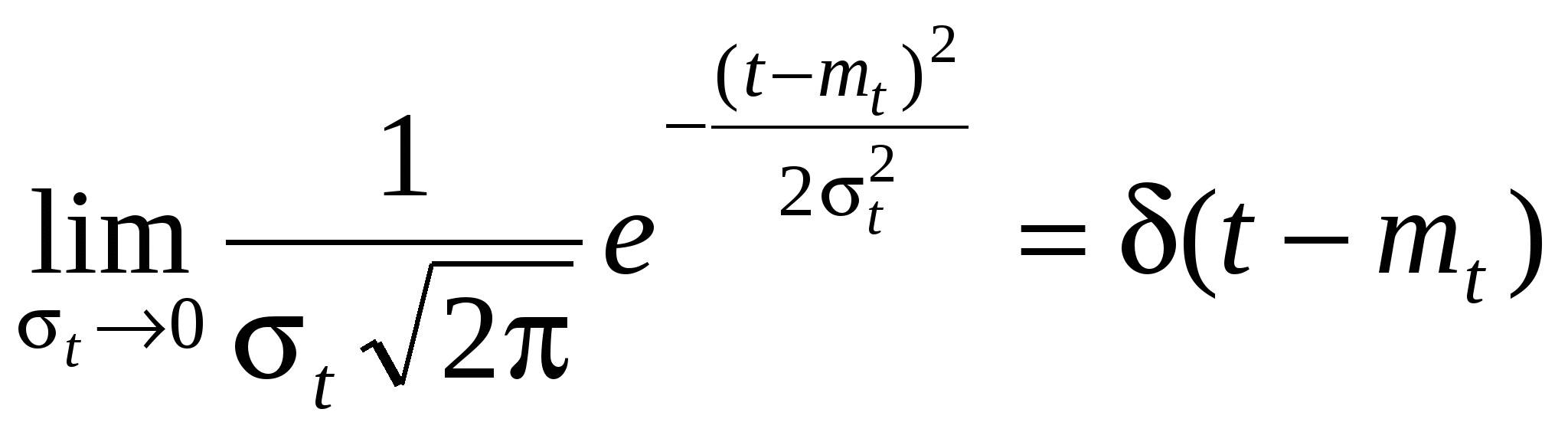ли выполняется условие  , то этот закон можно приближенно использовать. Устремим  . Тогда из (1.50) следует:  . (1.51)Плотность распределения интервала, на который случайным образом упала точка S: 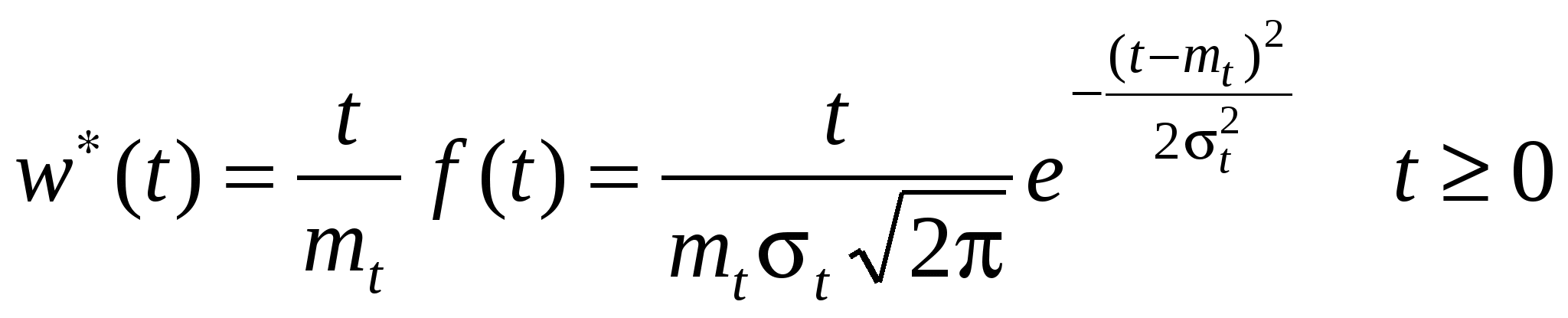 . (1.52)Соответственно плотность вероятности интервала от точки S до наступления очередного события имеет вид 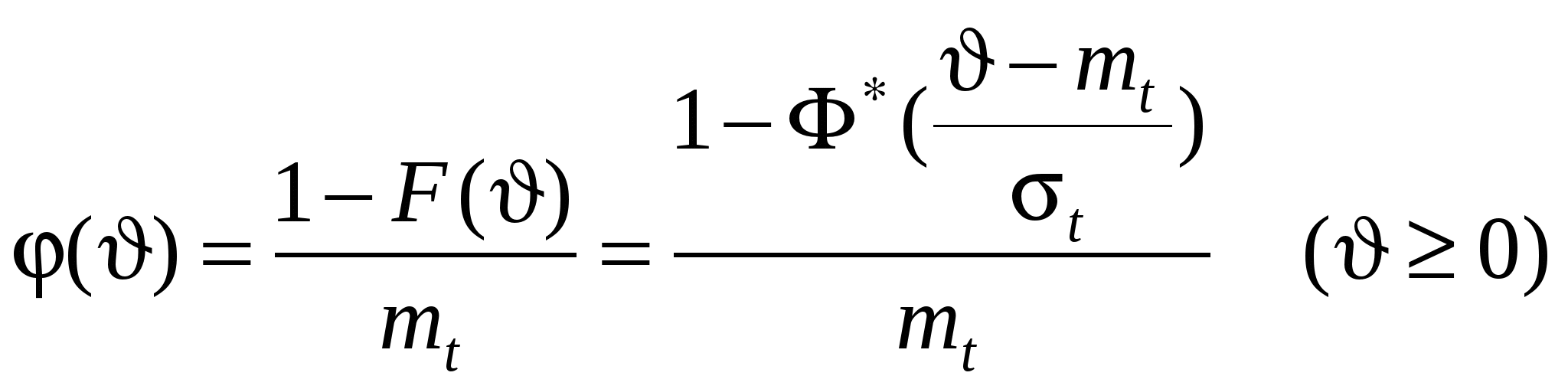 , (1.53)где  . (1.54)Характеристическая функция нормального распределения 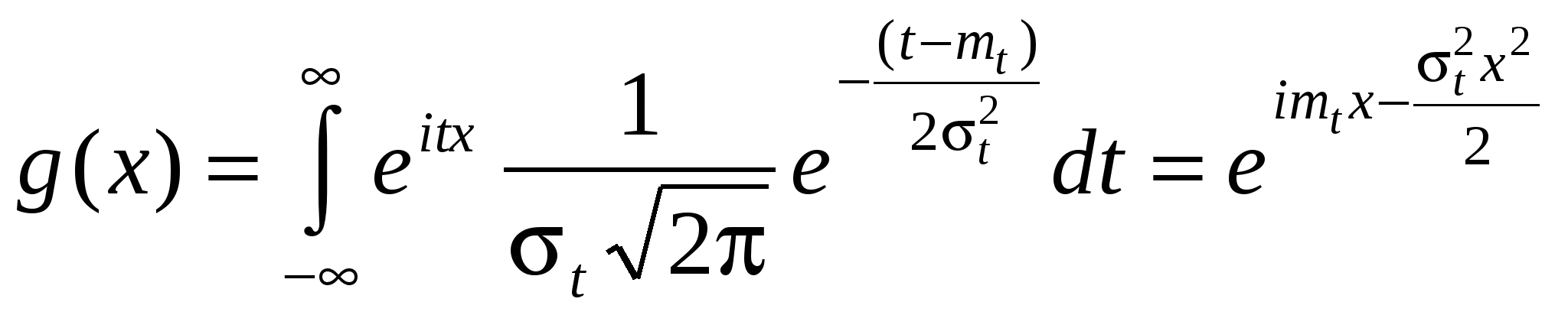 . (1.55)Поток Эрланга Поток Эрланга получается путём особого преобразования («разрежения») простейшего потока. Это преобразование осуществляется путём выбрасывания некоторых событий из простейшего потока. Процесс «разрежения» потока поясняется на рис.1.12, где буквой П обозначен простейший поток. Если выбрасывается каждая вторая точка, то получается Э1 – поток Эрланга первого порядка. Если выбрасывается два события подряд и оставляется каждое третье, то получается Э2 – поток Эрланга второго порядка и т.д. Потоком Эрланга k-го порядка называется поток Пальма, у которого интервалы между событиями представляют собой сумму (k+1) независимых случайных величин, распределённых одинаково по экспоненциальному закону с параметром  , где - интенсивность простейшего потока и   Рис.1.12. «Разрежение» простейшего потока. При  получается исходный простейший поток П. Для простейшего потока характеристическая функция интервала времени между соседними событиями определяется в виде  . Из свойств характеристической функции следует, что для суммы  независимых интервалов характеристическая функции будет иметь вид.  . Поэтому для Эk можно записать . Совершая обратный переход от характеристической функции к плотности вероятности, получим для Эk:  . (1.56)Функция распределения для этой плотности имеет вид  . (1.57)Соответственно числовые характеристики определяются как  , .При достаточно большом k (k>5) поток Эk можно считать приближённо нормальным. Это следует из того, что в Эk суммируется k+1 независимых величин (интервалов), распределённых одинаково, а такая сумма согласно центральной предельной теореме теории вероятностей (ЦПТ) при  асимптотически нормальна.Предельная теорема для суммарного потока. Суммарный поток получается в результате «сложения» потоков. Для простейших потоков П1 и П2 «сложение» состоит в том, что все моменты появления событий в этих потоках относятся к одной оси времени, на которой отмечаются моменты появления событий в суммарном потоке П1+П2=П.  Рис.1.13. Сложение простейших потоков. Как было установлено выше, для интенсивности суммарного потока справедливо:  , где n – число суммируемых потоков, а  - интенсивности суммируемых потоков. Предельная теорема для суммарного потока утверждает сходимость суммы независимых, ординарных, стационарных потоков к простейшему потоку. При этом условия, налагаемые на суммируемые потоки, приблизительно такие же, как и условия ЦПТ:
Сходимость к простейшему потоку осуществляется очень быстро (уже при  ). Зависимые потоки при сложение так же дают сходимость к простейшему потоку, но, естественно, при существенно большем числе слагаемых.Сложение нестационарных потоков даёт нестаци-онарный пуассоновский поток с интенсивностью  .Пуассоновский поток, как было показано выше, обладает устойчивостью (то есть при суммировании пуассоновских потоков вновь получается пуассоновский поток). Предельная теорема для редеющего потока. Рассмотрим специфическую операцию «разрежения» потока, когда событие переносится в разреженный поток с вероятностью p и, следовательно, отбрасывается с вероят-ностью  . Рис.1.14. поясняет такое разрежение потока, где обозначено: П–исходный поток (стационарный поток Пальма) и Пр – разреженный поток. Исследуем характеристики потока Пр. Для Тр справед-ливо:  , где случайные величины Тi взаимно незави-симы,z – случайная величина, представляющая собой число просуммированных интервалов. Найдем вероятность того, что случайное число z равно некоторому фиксированному k.  Рис.1.14. Вероятностное разрежение потока. Очевидно:  .Предположим z=k. Тогда при справедливости этой гипотезы характеристическая функция (условная) случайной величины Тр определяется как:  ,где g(x) - характеристическая функция случайной величины Тр. Безусловная характеристическая функция: 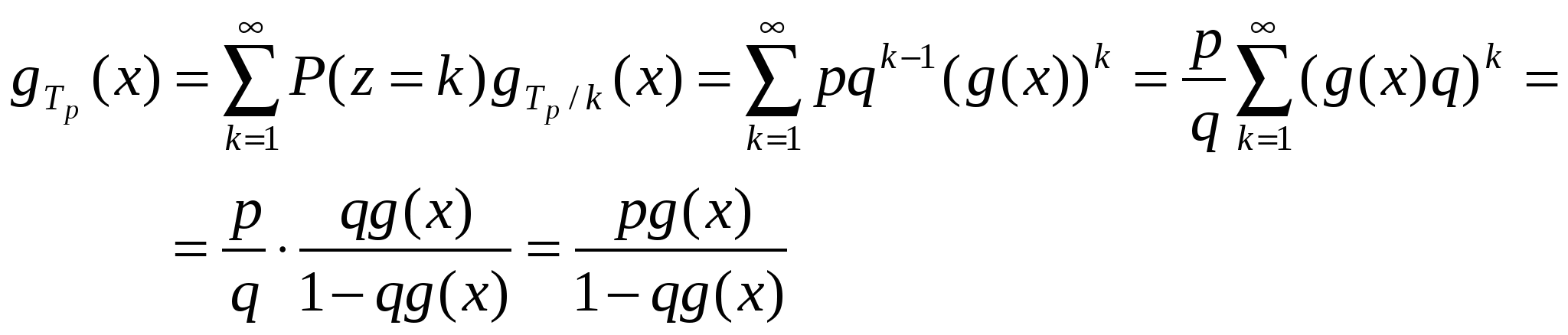 .Результат получен в предположении  и  с использованием формулы для суммы  членов геометрической прогрессии при  . (Если  - геометрическая прогрессия со знаменателем r , то  и  ). Зная  всегда можно найти плотность распределения  .Найдём числовые характеристики случайной величины Тр, но предварительно вычислим 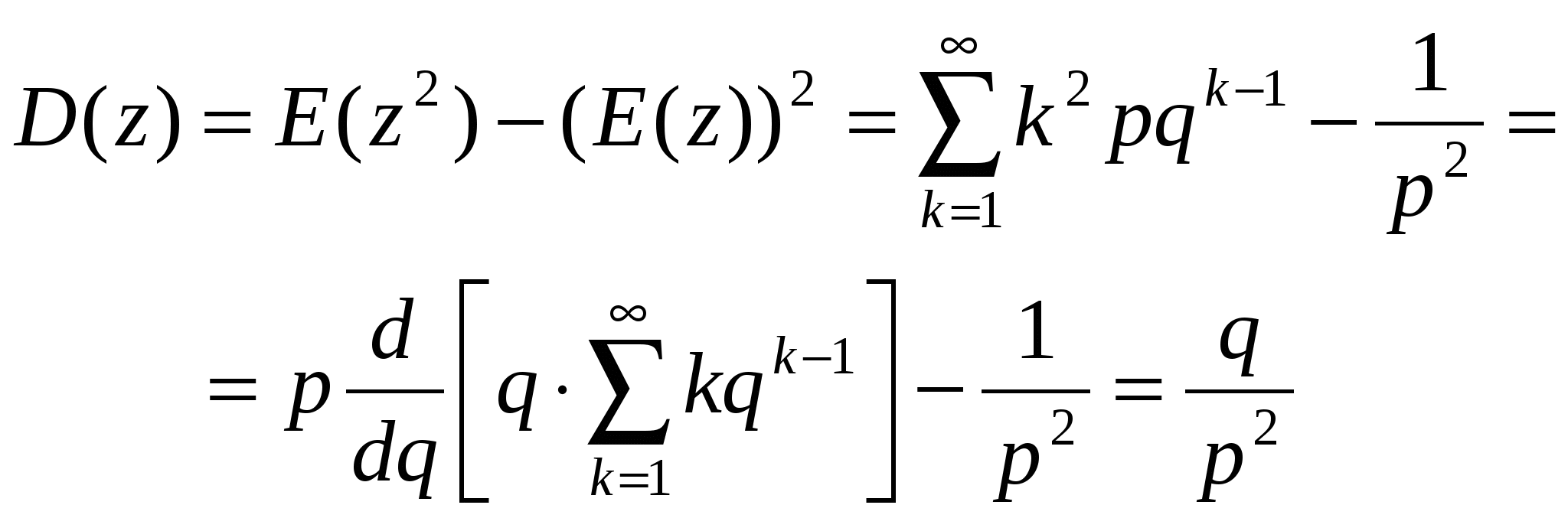 и  . . .Среднее  найдём через характеристическую функ-цию . Согласно (1.11): . , так как  .Итак  . Но  , поэтому:  . (1.58)Рассуждая аналогично, можно получить:  . (1.59)Очевидно, что интенсивность простейшего потока мож-но определить как  . Соответственно для разреженного потока с учетом (1.58) запишем  .Теперь можно перейти к предельной теореме для редеющих потоков. Смысл её состоит в том, что если последовательно разрежать ординарный стационарный поток Пальма достаточно большое число, то такой многократно разрежённый поток будет близок к простейшему. На практике уже  кратное разрежение (при р<0,8) даёт поток близкий к простейшему, даже если исходный поток был регулярным. |
),
не должны при 
становиться исчезающе малыми.