Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н.. В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие

• Название: В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие
• Анкор: Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н..doc
• Дата: 16.01.2018
• Размер: 379 Kb.
• Имя файла: Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н..doc
• Тип: Учебное пособие; #14313
• Категория: Геология
• страница: 10 из 12

4.4. Динамическая теория приливов

Исследование явления приливов показывает, что основное положение, принятое в статической теории, о равновесии поверхности океана в каждый момент времени не согласуется с достаточно быстрой сменой приливных явлений. Массы воды, обладая значительной инерцией, не могут приходить мгновенно в равновесие при изменении действующих сил.

Поэтому под действием непрерывно меняющейся периодической приливообразующей силы частицы воды, стремящейся к все новым и новым положениям равновесия, получают стремление перейти их (вследствие инерции водных масс) и в последующем совершать колебания около положения равновесия. Если бы приливообразующая сила прекратила свое действие, то колебания частиц воды, а, следовательно, и поверхности океана были бы затухающими (под действием силы трения). Но приливообразующие силы действуют непрерывно с определенным периодом. Поэтому и колебания поверхности океана незатухающие и также характеризуются известной периодичностью ⁵.

В 1775 году Лаплас предложил теорию движения жидкости, обладающей инерцией, на вращающейся Земле под действием периодически меняющейся приливообразующей силы, названную динамической теорией.

Допущения:

1. 
   Земля сплошь покрыта океаном постоянной глубины.
   
2. 
   Внутреннее трение и трение о дно отсутствуют.
   
3. 
   Вода однородна и несжимаема.
   

Принимая во внимание эти допущения, Лаплас установил закономерности, характеризующие зависимость между приливообразующей силой и колебаниями уровня моря. При определении этих колебаний Лаплас считал, что:

• 
  Период колебаний уровня моря, вызванный действием периодической приливообразующей силы, равен периоду этой силы;
  
• 
  Если одновременно действует несколько периодических сил, то колебания, вызываемые каждой из них, можно рассматривать раздельно, а общий результат действия всех сил получить путем суммирования составляющих колебаний.
  

Исходя из этих двух принципов, Лапласом впервые были получены уравнения движения приливов в океане постоянной глубины с учетом приливных сил, как внешней силы. Эти уравнения позволили объяснить происхождение лунных промежутков, независимо от влияния трения, а также фазовых и тропических неравенств. Важный вывод, полученный Лапласом, состоял в том, что им было показано решающее значение характера рельефа дна на приливы. Это дало толчок для математических исследований прилива в бассейнах различных форм.

Невозможность получить расчетную формулу для высоты прилива теоретически вызвала необходимость искать решение на основе сопоставления реального прилива и прилива, рассчитанного теоретически. Производя такое сопоставление, Лаплас пришел к выводу, что для получения расчетной формулы колебаний уровня необходимо ввести поправочные коэффициенты в амплитуду и фазу составляющих колебаний уровня. Эти поправочные коэффициенты оказываются постоянными для данного места и могут быть найдены, если имеются наблюдения над колебаниями уровня в данном месте.

Высота лунного прилива по статической теории определяется формулой:



Выразим косинус зенитного расстояния z_л (cos z_л) через широту места j, склонение Луны d и часовой угол t по известной формуле сферической тригонометрии:



После подстановки выраженного по этой формуле cos z_л в формулу высоты “статического” прилива и некоторых преобразований получим:



Это выражение будет справедливым для случая, когда океан покрывает всю Землю слоем одинаковой толщины, а вода представляет идеальную жидкость, лишенную инерции и сил внутреннего трения, то есть для статического прилива.

Каждое из трех слагаемых, заключенных в квадратные скобки, можно рассматривать как отдельные составляющие колебаний уровня, имеющие различный период.

1. 
   Первый член меняется весьма медленно вместе с изменением склонения Луны, следовательно, и силы, которые ему соответствуют, — это силы долгого периода. Лаплас предполагает, что поверхность океана под действием этих сил успевает занять положение равновесия, и ихпериодравен половине лунного месяца.
   
2. 
   Второй член изменяется главным образом вследствие изменения часового угла Луны t, а потому период соответствующих ему сил будет равен лунным суткам.
   
3. 
   Третьему члену, так как под знаком косинуса стоит удвоенное значение часового угла (Л)2t, соответствуют силы, имеющие период, равный лунным полусуткам.
   

Для получения формулы, пригодной для практических расчетов, Лаплас предложил ввести поправочные коэффициенты в амплитуду и фазу второго и третьего слагаемых, которые изменяются наиболее быстро. В первое слагаемое, изменяющееся медленно, Лаплас поправок не вводит, так как считает, что под его воздействием поверхность океана успевает занять положение равновесия.

Формула для расчета высоты прилива относительно среднего уровня моря принимает вид: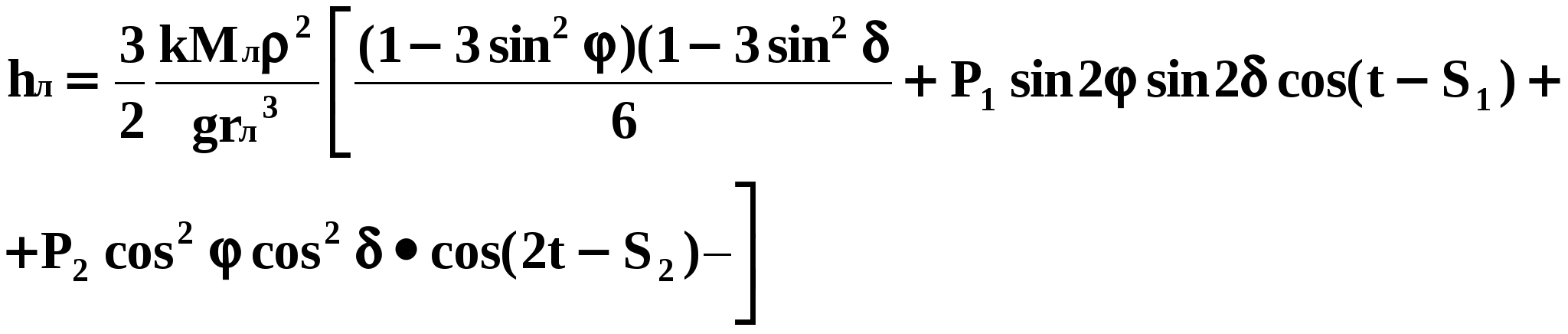



где:

Р₁, Р₂, S₁, S₂ — поправочные члены, определяемые из наблюдений над колебаниями уровня;

j — широта места;

d — склонение Луны;

t — часовой угол Луны;

k — гравитационная постоянная;

М_л — масса Луны;

r — расстояние до центра Земли (радиус Земли);

r_л — расстояние от центра Земли до центра Луны;

g — ускорение силы тяжести.

Полученная формула после определения поправочных членов может служить для предвычисления лунного прилива на любой день и час для того пункта, для которого определены коэффициенты⁶.

Аналогичное выражение может быть найдено и для солнечного прилива. Истинная высота прилива найдется как сумма лунного и солнечного приливов.

Каждое из слагаемых высоты в формуле Лапласа представляет элементарную волну.

1. 
   Первый член — волну долгого периода.
   
2. 
   Второй — суточного.
   
3. 
   Третий — полусуточного.
   

Полная расчетная формула Лапласа дает неплохие результаты при предвычислении правильных полусуточных приливов. Лаплас применял свою формулу для вычисления приливов в Бресте, а также для определения отношения приливообразующих сил Луны и Солнца. Поскольку приливы в Бресте имеют полусуточный характер, то Лаплас за малостью суточных волн вовсе пренебрег ими. В большинстве портов подобное упрощение не может быть сделано, так как суточные волны составляют заметную величину.

Вообще для других типов приливов, кроме правильных полусуточных, расчеты по этой формуле оказываются неудовлетворительными, так как сложные колебания уровня не могут быть представлены суммой только шести правильных косинусоид. Кроме того, формула Лапласа неудобна для практического расчета, потому что в нее не входит среднее солнечное время, что вызывает необходимость предварительно рассчитывать на заданный момент времени целый ряд вспомогательных величин: склонение, часовой угол, расстояние от центра Земли до центра Луны и Солнца.

Поэтому формула, полученная Лапласом, не получила практического применения.

Однако его принцип решения задачи был использован в методе гармонического анализа.

Выводы динамической теории Лапласа развивал Эри, исследуя распространение приливов в узких каналах. Исследования Эри (1845) получили название каналовой теории приливов. Соответственно постановке задачи полученные Эри результаты действительно характеризуют приливы в районах, которые близки к каналам. Для объяснения приливов в океанах выводы каналовой теориинеприложимы.

Улучшение в теорию Лапласа внес Хоф, который при своих исследованиях учитывал влияние отклоняющей силы вращения Земли (силы Кориолиса) и возникающие свободные волны. В этой теории, так же как и в теории Лапласа, принимается, что океан покрывает всю Землю. Выводы теории показывают, что решающее влияние на величину прилива имеет период свободных колебаний водной толщи, определяемый глубиной моря и влиянием вращения Земли.

Результатом исследований Хофа, Гольдсбоу и Дудсона явились сведения в динамических возвышениях приливов различных периодов по отношению к высоте статических приливов.

Каналовая теория Эри (1845), рассматривавшая движение приливной волны в каналах постоянного сечения, различно ориентированных относительно географической системы координат, позволила установить, что: в каналах, ориентированных по параллелям, образуются поступательные волны, а в меридиональных каналах — стоячие волны.