Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н.. В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие

• Название: В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие
• Анкор: Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н..doc
• Дата: 16.01.2018
• Размер: 379 Kb.
• Имя файла: Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н..doc
• Тип: Учебное пособие; #14313
• Категория: Геология
• страница: 12 из 12

V. Методы предвычисления приливов

Фундаментальные основы теории приливов, сформированные Ньютоном и Лапласом, свидетельствуют о практической невозможности получения расчетных формул для предвычисления приливов в реальном океане. Однако они позволили определить наиболее эффективные пути решения задачи при использовании результатов непосредственных наблюдений над уровнем моря. Наиболее плодотворным оказался путь, указанный Лапласом, который по существу, предложил применить к предвычислению приливов метод гармонического анализа.

Метод гармонического анализа был в дальнейшем развит Томсоном (Кельвином) и Дарвином. Его можно считать основным методом предвычисления приливов, используемым и в настоящее время.

В 1936 году Дудсон и Варбург предложили упрощенный метод гармонического анализа, получивший название штурманского метода.

Идея гармонического анализа основывается на двух постулатах Лапласа и заключается в том, что сложная кривая изменения приливного уровня под действием приливообразующих сил Луны и Солнца может быть в каждом пункте побережья, представленное как сумма правильных гармонических кривых (или волн) вида:

, где

h — высота прилива;

R — амплитуда волны;

q — угловая скорость волны, величина постоянная для каждой волны и не зависящая от физико-географических условий;

t — среднее солнечное время;

Е — начальная фаза волны.

Гармонические составляющие прилива можно представить как результат действия воображаемых фиктивных светил, каждое из которых обращается по своей орбите в плоскости экватора и со своей угловой скоростью.

Суммарный лунно-солнечный прилив можно представить состоящим из множества простых правильных колебаний, вызываемых многими фиктивными светилами. Подобрав массы фиктивных светил, их радиусы орбит и угловые скорости, можно получить совокупный результат, описывающий реальные колебания приливного уровня. Тогда высота уровня лунно-солнечного прилива в любой момент времени будет определяться как сумма:

, где

z₀ — высота среднего уровня над нулем (0) глубин.

Учитывая влияние местных условий на амплитуду прилива R, ее можно выразить как:

, где

Н — средняя амплитуда волны, зависящая от местных физико-географических условий и постоянная для данного пункта;

f — редукционный множитель, зависящий от астрономических условий и рассчитываемый по законам движения светил.

Начальная фаза волны Е представляется как сумма двух слагаемых:

, где

(V₀ + U) — начальный астрономический аргумент, представляющий часовой угол фиктивного светила на 0 часов. Он рассчитывается на 0 часов первого дня наблюдений или предвычислений прилива по законам движения светил. Значения астрономического аргумента и редукционного множителя приводятся в соответствующих “Руководствах” по обработке наблюдений над колебаниями уровня моря.

g — угол положения волны, зависящий от местных физико-географических условий и являющийся для данного пункта величиной постоянной.

f, q, (V₀+U) — зависят только от астрономических условий и могут быть вычислены на любой срок вперед.

H и g определяются на основе обработки наблюдений над колебаниями уровня в данном пункте. Так как для данного пункта эти величины постоянны, то их называют гармоническими постоянными, а процесс их определения путем обработки данных наблюдений в данном пункте называется гармоническим анализом.

Формула для расчета высоты прилива методом гармонического анализа может быть представлена в следующем ви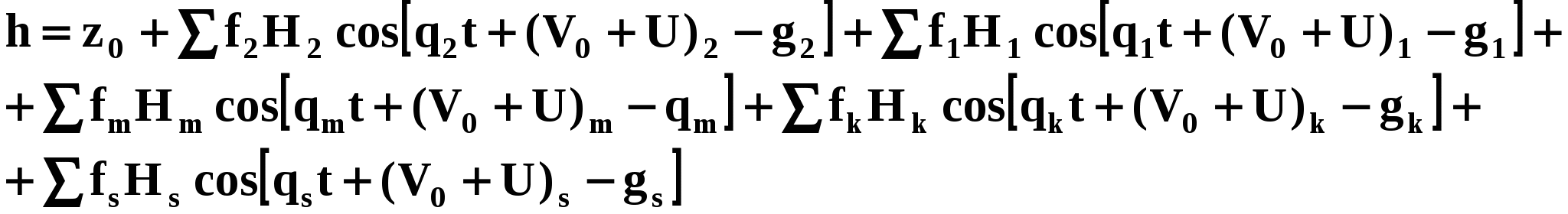де:

где:

z₀ — высота среднего уровня моря в данном пункте над принятым нулем глубин.

Индексы при перечисленных аргументах означают:

2 — составляющие волны, имеющие период, близкий к половине суток — полусуточные волны;

1 — составляющие волны суточного периода;

m — мелководные составляющие волны прилива;

k — сложные лунно-солнечные составляющие волны прилива;

s — составляющие волны долгого периода (полугодового, годового, многолетнего).

Процесс определения высот уровня на будущие моменты времени называются предвычисление прилива.

Приведенная формула — самая простая формула для вычисления приливов адмиралтейским методом.

Полная формула для расчета высоты прилива имеет 93 слагаемых (волны). Однако практически оказывается, что нет необходимости вычислять гармонические постоянные всех 93 членов формулы. С достаточной для практики точностью можно предвычислять приливы, используя только 8-11 основных слагаемых волн прилива.

Полусуточные и суточные волны называются главными волнами. Вклад в суммарную высоту прилива каждый из составляющих волн прилива характеризуется значением коэффициента, который представляет величину отношения амплитуды данной волны к суммарной амплитуде прилива.

В океанографической практике для вычисления гармонических постоянных принят метод Дарвина. В нем гармонические постоянные волн прилива рассчитываются по ежечасным наблюдениям над колебаниями уровня прилива за 15 и 30 суток. При 30-суточной серии определяются гармонические постоянные всех 11 основных волн. При 15-суточной серии наблюдений непосредственно из наблюдений определяются гармонические постоянные 6 волн.

В 1936 году в Англии Дудсон и Варбург разработали упрощенный метод гармонического анализа и назвали его “адмиралтейским”. В СССР он получил название штурманского метода. В основу его положено вычисление гармонических постоянных из ежечасных наблюдений за колебаниями уровня за 1-2 суток. Этот метод позволяет:

1. 
   Предвычислять уровень на любой час по гармоническим постоянным 4 основных составляющих волн прилива:
   

• 
  М₂ — главная лунная полусуточная волна:
  
• 
  S₂ — главная солнечная полусуточная волна:
  
• 
  К₁ — лунно-солнечная деклинационная суточная волна:
  
• 
  О₁ — главная лунная суточная волна.
  

1. 
   Вычислять гармонические постоянные четырех основных волн прилива (М₂, S₂, К₁, О₁) из суточной или двухсуточной серии ежечасных наблюдений над уровнем.
   
2. 
   Предвычислять на любой день моменты и высоты полных и малых вод по гармоническим постоянным указанных четырех волн, без промежуточных расчетов высоты прилива на каждый час.
   

Штурманский метод основан на возможности объединения волн, близких по периоду, когда не требуется очень высокой точности предвычисления уровня. В штурманской практике эта точность составляет 0,1 м. Поэтому штурманский метод наиболее удобен в корабельных условиях, тем более, что предвычисления приливов этим методом требует мало времени и достаточно просты.

Четыре главные волны (М₂, S₂, К₁, О₁) наиболее подвержены влиянию местных условий. Гармонические постоянные четырех других волн (N₂, K₂, P₁, Q₁) оказывается возможным выразить через гармонические постоянные главных волн. Поэтому высоту прилива можно выразить вместо суммы восьми суммой четырех составляющих волн (М₂, S₂, К₁, О₁). Для учета влияния остальных четырех волн вводятся поправки в амплитуды и фазы главных волн. Эти поправки оказываются переменными, зависят от астрономических условий и поэтому могут быть рассчитаны заранее и сведены в таблицы. Такие таблицы приводятся в руководствах по обработке и предвычислению приливов.

С учетом этих поправок расчетная формула для высоты прилива принимает вид: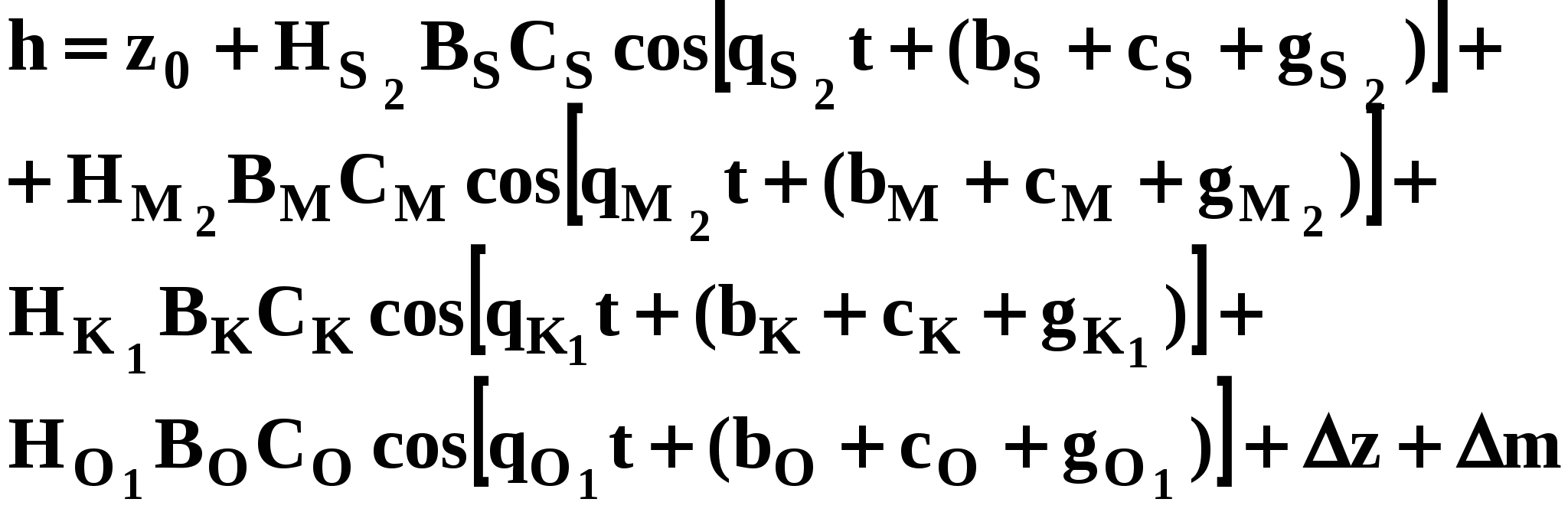



где:

Н, g —гармонические постоянные главных волн;

В, b — астрономические поправки в амплитуду и фазу главных волн, выбираемые из таблиц по году и дате;

С, с — астрономические поправки в амплитуду и фазу главных волн, выбираемые по моменту кульминации Луны на меридиане Гринвича и ее горизонтальному параллаксу;

t —время на часах;

q — угловые скорости отдельных составляющих волн приливов;

Δz — сезонная поправка среднего уровня моря;

Δm — поправки элементов приливов для учета влияния мелководья;

z₀ — высота среднего уровня над нулем глубин.

По этой формуле решается задача предвычисления высоты прилива штурманским методом на заданный час.

VI. Характер распределения приливов в Мировом океане

Данные наблюдений, имеющиеся на сегодняшний день, о характере и величине приливов в Мировом океане относятся только к его побережью. В открытых районах океанов наблюдений над приливами нет.

А.И.Дуванин составил карту характера и наибольших величин приливов на основе наблюдений над уровнем. Она показала, что в океане преобладают полусуточные приливы. Они наблюдаются почти везде у побережий Атлантического, Индийского и Северного Ледовитого океанов.

В Тихом океане преобладают смешанные приливы, здесь же отмечается и большинство мест с суточными приливами.

Величина прилива зависит от конфигурации берега, от характера бассейна. Поэтому величины приливов отличаются большим разнообразием. В морях, связанных с океанами узкими проливами (Балтийское, Средиземное, Японское), величины приливов обычно не превышают 50 см или отсутствуют. В Черном море прилив наблюдается в пределах 8 см. В открытых районах океана у берегов островов величина приливов составляет около 1 м.

По мере приближения к берегу, величина приливов возрастает под влиянием конфигурации берега, уменьшения глубины. Особенно интенсивное возрастание величины пролива отмечается там, гдепериод собственных колебаний бассейна близок к периоду приливной волны, что обусловлено резонансом.

В проливах, вершинах заливов, устьях рек бывают приливы более 6 м высотой. В воронкообразных заливах приливы могут возрастать до гигантских значений (залив Мэн, бухта Фанди — 18 м – максимальная величина прилива в Мировом океане).

В России наибольшая величина прилива в Пенжинской губе (залив Шелихова) — 13,3 м. В Белом море в Мезенском заливе — 10 м. В западной Европе в проливе Ла-Манш — 7 м, в устье реки Ранс — 8-9 м.

Величина прилива возрастает обратно пропорционально корню четвертой степени из глубины моря и обратно пропорционально квадратному корню из ширины бассейна.

По расчетам Ганзена, в Атлантическом океане приливная волна движется со стороны Антарктики, в северной части океана, у Ньюфаундленда возникает амфидромия, которую приливная волна оббегает против часовой стрелки. Дитрихпо методу Дефанта определил также амфидромию в южной Атлантике, две — в Индийском и три — в Тихом океанах. Приливная волна огибает амфидромии в Северном полушарии против часовой стрелки, в Южном полушарии — по часовой стрелке.

Литература

1. 
   Атлас океанов. Тихий океан, 1974; Атлантический и Индийский океан, 1978; Северный Ледовитый океан, 1980. ГУНИО МО СССР.
   
2. 
   Богданов Д.В. Региональная физическая география Мирового океа­на - М.: Наука, 1985. - 176 с.
   
3. 
   Богданов К. Т. Приливы Мирового океана. - М.: Наука, 1975. - 165 с.
   
4. 
   Гембель А.В. Общая география Мирового океана : Учеб. по­собие для географ. специальностей вузов. - М.:Высшая школа, 1979. - 215 с.
   
5. 
   Дитрих Г. Общая океанография. - М.: ИЛ, 1962. - 160 с.
   
6. 
   Дуванин А. И. Волновые движения в море. - Л.: Гидрометеоиздат, 1968. - 223 с.
   
7. 
   Дуванин А. И. Приливы в море. - Л.: Гидрометеоиздат, 1960. - 187 с.
   
8. 
   Егоров Н. И. Физическая океанография. - Л.: Гидрометеоиздат, 1974. - 455 с.
   
9. 
   Жуков Л.А. Общая океанология. - Л.: Гидрометеоиздат, 1976. - 376 с.
   
10. 
    Зубов Н. Н. Динамическая океанология. - Л.: Гидрометеоиздат, 1947. - 346 с.
    
11. 
    Картер С. Королевство приливов. - Л.: Гидрометеоиздат, 1977. - 112 с.
    
12. 
    Леонтьев О.К. Физическая география Мирового океана.- М.: Изд-во МГУ, 1982. - 200 с.
    
13. 
    Марчук Г. И., Каган Б. А. Океанские приливы. - Л.: Гидрометеоиздат, 1977. - 406 с.
    
14. 
    Наука об океане / Под ред. О.И. Мамаева. - М.: Прогресс, 1981. - 392 с.
    
15. 
    Некрасов А. В. Приливные волны в окраинных морях. - Л.: Гидро-метеоиздат, 1975. - 299 с.
    
16. 
    Ржонсницкий В. Б. Приливные движения. - Л.: Гидрометеоиздат, 1979. - 243 с.
    
17. 
    Ржонсницкий В. Б. Проблемы каналовой теории приливов. - Л.: Гидро-метеоиздат, 1973. - 157 с.
    
18. 
    Физическая география Мирового океана (Серия: "География Мирового океана").- Л.: Наука, 1980 . - 362 с.
    
19. 
    Шамраев Ю. И., Шишкина Л. А. Океанология. - Л.: Гидрометеоиздат, 1980. -195 с.
    
20. 
    Шокальский Ю. М. Океанография. - Л.: Гидрометеоиздат, 1959. - 633 с.
    
21. 
    Шулейкин В. В. Краткий курс физики моря. - Л.: Гидрометеоиздат, 1959. - 589 с.
    

1 Не путать термины “прилив” и “приливы”. Приливы” — приливные колебания уровня в Мировом океане.

2 Это обращение Луны вокруг Земли, как и обращение Солнца, — кажущееся, возникающее вследствие вращения Земли вокруг своей оси.

3 В отношении суточных приливов с одной полной и одной малой водами в сутки понятие о суточном неравенстве смысла не имеет.

4 В действительности приливообразующая сила в зените на 1/43 больше, чем в надире.

5 Недостатком статической теории является то, что в ней рассматривается действие только приливообразующих сил. Между тем существенное значение в движении приливных волн в Мировом океане имеют еще:

1. 
   Градиенты давления.
   
2. 
   Отклоняющая сила вращения Земли.
   
3. 
   Сила трения между движущейся водой и дном бассейнов.
   

Проявление этих вторичных сил начинается только после возникновения движения, которое в случае приливов вызывается действием приливообразующих сил.

6 С их помощью теоретически рассчитанный прилив приводится в согласие с наблюдающимися в природе.

7 Если смотреть в направлении распространения волны, то в Северном полушарии вода в гребне волны будет прижиматься к правой стороне, а в подошве — к левой стороне канала. На правой стороне будут и более сильные течения, достигающие своего максимума на гребне и подошве волны. Такая свободная длинная волна, распространяющаяся в узком длинном канале, называется волной Кельвина.

r