Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н.. В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие
 Скачать 379 Kb.
|
IV. Основы теории приливов4.1. Приливообразующие силы и их потенциалНа каждую частицу Земли действуют:
Сила притяжения к центру Земли (1) и центробежная сила при вращении Земли вокруг своей оси (2) постоянны во времени, их равнодействующая является силой тяжести. Поскольку сила тяжести для данной точки Земли является величиной постоянной, она не участвует в создании прилива и поэтому ее можно не учитывать. Силы притяжения Луны и Солнца в отдельных точках Земли неодинаковы (переменны) и зависят от расстояния от этих точек до центров соответственно Луны и Солнца. Центробежные силы систем Земля — Луна и Земля — Солнце для каждой точки Земли одинаковы и равны силам притяжения Луны и Солнца, но только в центре Земли. Это вполне понятно, так как в противном случае расстояние между Землей и Луной и Землей и Солнцем или увеличивалось бы или уменьшалось. Равнодействующая всех сил, действующих на частицу Земли, оказывается переменной. Для простоты рассуждения положим, что на частицу Земли действует только приливообразующая сила Луны, и рассмотрим вначале только взаимодействие в системе Земля — Луна (приливообразующая сила Солнца выводится аналогично) вокруг их общего центра тяжести. При этом суточное вращение Земли и движение всей системы вокруг Солнца во внимание не принимается. Общий центр тяжести между Землей и Луной находится на расстоянии 0,73 земного радиуса, то есть внутри тела Земли. (В системе Земля — Солнце общий центр тяжести системы лежит внутри Солнца). Система Земля — Луна совершает полный оборот вокруг общего центра тяжести за лунный месяц (27 1/2 суток). 4.1.1. Приливообразующие силы
 Возьмем систему прямоугольных координат с началом в центре Земли. Поместим координатную плоскость ХОY так, чтобы она совпала с плоскостью экватора, а ось Z направим вертикально вверх. Пусть масса Луны — Мл, а точка Р на поверхности океана — некоторая его частица, массу которой положим равной единице, координаты ее — (х,у,z), расстояние от нее до Луны — D, а до центра Земли — r (радиус Земли). Расстояние от центра Земли до центра Луны — rл, zл — приведенное к центру Земли зенитное расстояние Луны (угол между направлением на Луну и точку Р из центра Земли). Рассмотрим силы притяжения Луны, действующие на частицы с массой, равной единице, находящиеся в центре Земли и на ее поверхности в точке Р. Z  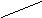  Y Рис. 7. К выводу потенциала приливообразующих сил Согласно 1-му закону Ньютона, сила притяжения пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними. Поэтому на частицу, находящуюся в точке Р1 будет действовать сила притяжения Fp, равная по величине: Fр = kMл / D2, а на частицу, расположенную в центре Земли (О), сила притяжения F0; Fo = kMл / rл2, где k — коэффициент пропорциональности, называемый гравитационной постоянной. Силы притяжения к Луне частиц на поверхности океана и в центре Земли неодинаковы, так как удаление их от центра притяжения Луны различно. Сила притяжения, действующая на частицы, находящиеся в центре Земли (в точке О), равна по величине центробежной силе Fц, возникающей от обращения системы Земля — Луна вокруг их общего центра тяжести, но обратна ей по направлению. В векторной форме это запишется так:  Силы притяжения Луны, действующие на частицы, расположенные вне центра Земли, не уравновешены центробежной силой. Поэтому эти частицы будут смещаться относительно центра Земли. В результате в каждой точке Земли вследствие геометрического сложения силы притяжения Луны в данной точке  и центробежной силы  возникает равнодействующая, которая и является приливообразующей силой  : |
