Приливы в Мировом океане - Безруков Ю.Ф., Тамайчук А.Н.. В. И. Вернадского Географический факультет Кафедра физической географии и океанологии Ю. Ф. Безруков, А. Н. Тамайчук Приливы в Мировом океане Учебное пособие
 Скачать 379 Kb. Скачать 379 Kb.
|
4.3. Статическая теория приливовВ 1687 году Ньютон на основе закона всемирного тяготения предложил первую теорию приливов — статическую теорию (а также решил задачу расчета потенциала приливообразующих сил, приведенную ранее). Статическая теория имеет ряд недостатков и непригодна для предвычисления приливов, однако все же позволяет качественнообъяснить некоторые особенности явления приливов. Допущения статической теории:
Потенциал силы тяжести представляет функцию, производная от которой по направлению нормали к поверхности равных значений потенциала — изопотенциальной поверхности равна силе тяжести. Для единичной массы выражение потенциала силы тяжести Г запишется следующим образом: g — ускорение силы тяжести, равное по величине силе тяжести единицы массы; h — направление нормали к изопотенциальной поверхности. Из этого соотношения получим выражение потенциала силы тяжести: Потенциал силы тяжести на среднем уровне обычно принимается равным нулю. Тогда потенциал силы тяжести представляет собой работу, совершаемую против силы тяжести, при перемещении единицы массы от среднего уровня на высоту h. Из допущения статической теории (так как приливообразующая сила уравновешена силой тяжести) в каждый момент времени должно удовлетворяться равенство: (Потенциал силы тяжести равен полному потенциалу приливообразующих сил Луны и Солнца). Подставив значение потенциала силы тяжести, получим: откуда Для определения высоты прилива необходимо в эту формулу подставить значения потенциалов приливообразующих сил Луны и Солнца. Тогда получим: Анализ этой формулы показывает, что если бы действовала только приливообразующая сила Луны, то поверхность океана приняла бы форму эллипсоида вращения, большая ось которого была бы направлена на Луну. В случае действия одного Солнца большая ось эллипсоида вращения была бы направлена на Солнце. При одновременном действии Луны и Солнца поверхность океана можно получить геометрическим суммированием лунного и солнечного эллипсоидов вращения. По формуле статической теории приливов можно подсчитать, что при среднем расстоянии Земли от Луны и Солнца должны были бы наблюдаться следующие величины лунных и солнечных приливов: hл = 0,54 м; hс = 0,25 м. Следовательно, для сизигийных приливов: В этих же условиях для квадратурных приливов: Максимальная величина сизигийного прилива оказывается равной 0,9 м. Минимальная квадратурного — 0,2 м. Близкие к рассчитанным по статической теории величины приливов наблюдаются у побережий островов в открытом океане. Это говорит о том, что различие в величинах прилива у берегов континентов создается вследствие влияния физико-географических условий района. На основании статической теории можно дать объяснение полумесячным, месячным и суточным неравенствам. Полумесячное фазовое неравенство приливов объясняется, наблюдающимся в течение полумесяца постепенным смещением лунного и солнечного приливных эллипсоидов друг относительно друга. В дни сизигии Луна и Солнце кульминируют одновременно, лунный и солнечный эллипсоиды прилива складываются, поэтому подъем уровня, вызванный действием Луны, увеличивается за счет действия Солнца. Понижение уровня при отливе, равно сумме понижений, производимых Луной и Солнцем. Следовательно, величина прилива будет наибольшей — сизигийный прилив. В квадратуры большие оси лунного и солнечного эллипсоидов взаимно перпендикулярны и эллипсоиды вычитаются. Так как лунный прилив больше солнечного, то результирующий эллипсоид будет направлен большой осью на Луну, однако высота подъема уровня под действием Луны будет уменьшенаотливом, вызываемым Солнцем. Высота же малой воды будет увеличена приливом под действием Солнца. Прилив будет наименьшим — квадратурный прилив. Гребень волны суммарного лунно-солнечного прилива всегда лежит ближе к гребню лунного прилива, так как последний в два раза больше солнечного. Поэтому удобнее определять время наступления полной воды по отношению к моменту кульминации Луны, а не Солнца. В дни сизигии, когда оба светила кульминируют в одно время, моменты полных вод, вызываемых ими приливов, совпадают, и полная вода суммарного прилива должнанаступить одновременно с кульминацией Луны. В действительности и в это время моменты полной воды и кульминации Луны отстоятдруг от друга на среднее значение лунного промежутка. Объяснения этому явлению статическая теория не дает (по А.И.Дуванину). По мере того, как Луна отстает в своем движении от Солнца (на 50 минут в сутки), полные воды лунного и солнечного приливов будут смещаться относительно друг друга, и моменты полной воды суммарного прилива будут удаляться от момента кульминации Луны (происходит смещение времени суммарного прилива от времени лунного прилива. Это объясняет полумесячное изменение лунных промежутков за счет фазового неравенства). 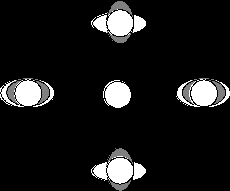 Рис. 8. Сочетания лунного и солнечного приливов, объясняющие возникновение сизигийного и квадратурного приливов В квадратуре, когда разность между кульминациями Луны и Солнца достигнет 6 часов, момент наступления полной воды суммарного прилива вновь совпадет (по статической теории, но в действительности это не так) с кульминацией Луны. 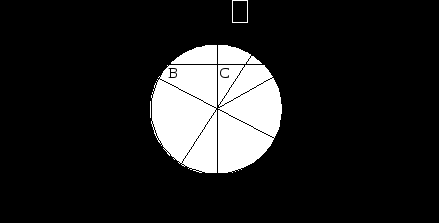 Рис. 9. Суточное неравенство приливов, зависящее от склонения светила Когда разность превысит 6 часов, момент полной воды суммарного прилива снова будет удалятьсяот момента кульминации Луны до следующей сизигии. Суточные и полумесячные неравенства в суточных приливах обусловлены склонением Луны. В свете выводов статической теории можно рассмотреть также механизм возникновения суточных неравенств. Пусть РР1 — ось вращения Земли, ЕQ — экватор, ZN — направление на Луну, DF — круг освещения. Согласно статической теории большая ось эллипсоида вращения, характеризующего поверхность океана, направленное на Луну, для наблюдателя, находящегося в точке А, полная вода наступит в момент верхней кульминации Луны. Малая вода наступит для него тогда, когда точка А вследствие вращения Земли придет на круг освещения (в точку С). Это случится не через 6 часов 12 минут после полной воды, а позже, потому что дуга параллели АС составляет больше четверти окружности. Следующая после малой полная вода наступит, когда наблюдатель будет в точке А’, через 12 часов 25 минут после первой полной воды, но менее чем через 6 часов 12 минут, после предшествовавшей малой воды, так как дуга СА’ меньше четверти окружности. При этом полная вода в А будет иметь большую высоту, чем в А’. После полной воды A’ следующая малая наступит скорее, чем через 6 часов 12 минут, когда наблюдатель вновь будет на круге освещения. Через 24 часа 50 минут после первой полной воды наблюдатель снова будет в точке А, и будет снова полная вода. Для других мест земного шара высоты полных вод при верхней и нижней кульминации Луны также неодинаковы, так как приливный эллипсоид расположен несимметрично относительно оси вращения Земли. Только на экваторе обе полные воды будут одинаковой высоты, то есть суточных неравенств не будет при любом склонении Луны, а наибольшие приливы будут при склонении Луны равном нулю. На полюсах уровень в течение суток меняться не будет, то есть прилив будет отсутствовать. Будут отличаться только колебания уровня с периодом, равным половине лунного месяца. Таким образом, в те дни, когда склонение Луны не равно нулю суточное неравенство в высоте сопровождается неравенством во времени, вследствие которого первая малая вода наступает позже, чем через 6 часов 12 минут после предшествующей полной, а вторая — раньше. Для солнечных приливов период суточного тропического неравенства равен полугоду, так как в течение этого времени Солнце возвращается к экватору. Месячные (параллактические) неравенства обусловлены изменением расстояния от Земли до Луны. Из формулы статической теории следует, что высота прилива обратно пропорциональна кубу расстояния между центром Земли и центром возмущающегося светила. Поэтому высота прилива при наименьшем расстоянии — в перигее, оказывается больше, чем при наибольшем — в апогее для Луны на 30%, а для Солнца на 10%. Недостаткистатической теории приливов:
Статическая теория, давая объяснения некоторым особенностям в явлении прилива с качественной стороны, не пригодна для практических расчетов. Причина этого заключается в том, что допущения, лежащие в основе теории, не соответствуют действительности. Статическая теория объясняет лишь действие космических сил, то есть причины, вызывающей приливные движения, поведение же самих приливов она не объясняет. Мы допускали, что океан покрывает Землю слоем постоянной глубины, что океан неподвижен, статичен, но знаем, что это не так, что он динамичен и изменчив. Существуют факторы на самой Земле, которые никак или почти никак не связаны с астрономией, но оказывают огромное влияние на приливы. Выводы (о силах, вызывающих приливы):
То же справедливо и для Солнца. Когда же Солнце и Луна находится над экватором или вблизи от него, их приливообразующие силы являются полусуточными. |
