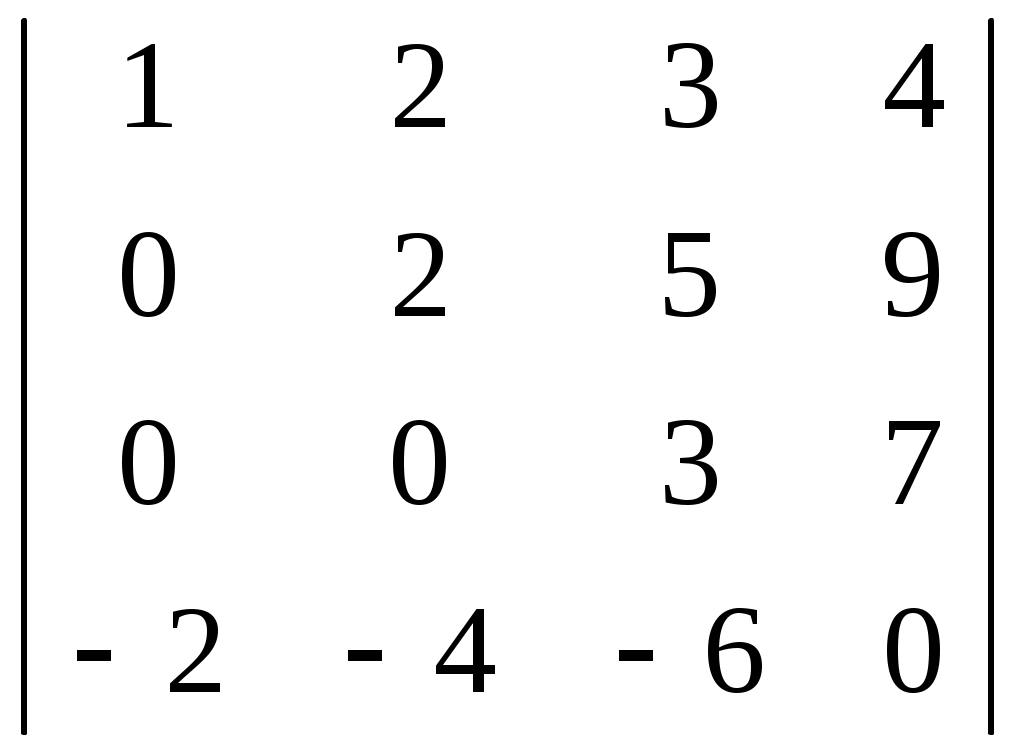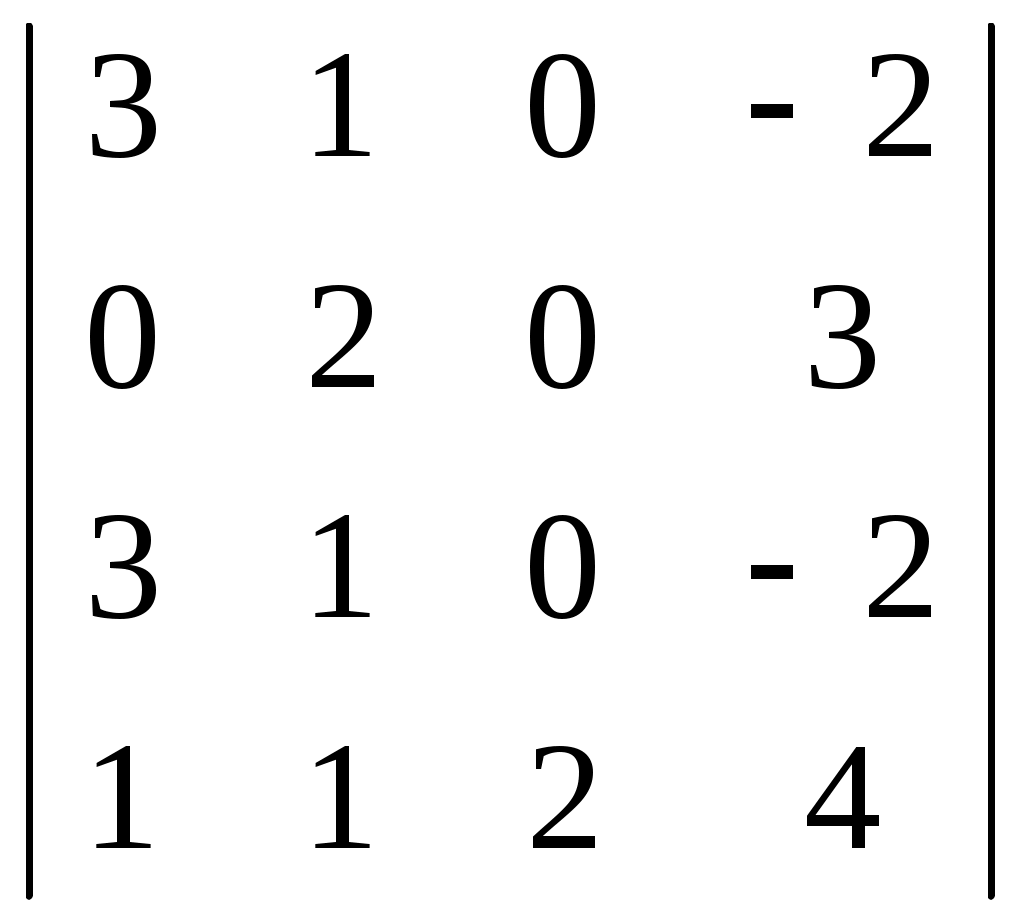Синергия Математика. В матрицах жирным отмечены элементы правильного ответа!

• Название: В матрицах жирным отмечены элементы правильного ответа!
• Дата: 08.05.2022
• Размер: 1.11 Mb.
• Имя файла: Синергия Математика.doc
• Тип: Документы; #517476
• страница: 3 из 6

Используя свойства определителя, вычислить определитель – см. «Определитель …равен»

Какая из заданных функций задана явно:

+ y = sinx

exy = 3

xy = 5

lg(x + y) = 5

x2 + y2 = 9

Какая из заданных функций является обратной для функции Y = 5x – 3:



Касательная к графику функции y = x² в точке M₀(1; 1) определяется уравнением

y = 2x – 1

Матрица, являющаяся произведением матриц

A = , B = ,

будет иметь размерность

3 x 2

Минор элемента x определителя … равен …

Определитель	Минор
	-2
	-2

Наибольшим значением функции y = x² – 2x на отрезке [-1; 1] является …

3
Наибольшим значением функции y = – x² + 2x на отрезке [-1; 2] является …

1

Найти все точки разрыва функции – см. «Точками разрыва заданной функции …»

Найдите вторую производную функции …

Функция	Производная
y = sin2x	- 4 sin2x

Найти интеграл – см. «Интеграл … равен …»

Найти интервалы монотонного возрастания функции y = 6x² – 3x.

(1/4; +∞)

Найти обратную матрицу для матрицы A = …

Матрица	Обратная матрица
	A-1 =
	A-1 =
	A-1 =
	A-1 =
	A-1 =

Найти объем тела, полученного от вращения плоской фигуры … – см. «Объем тела, полученного от вращения плоской фигуры ...»

Найти площадь плоской фигуры, ограниченной линиями … – см. «Площадь плоской фигуры, ограниченной линиями …, составит …»

Найти площадь плоской фигуры, ограниченной линиями … вокруг оси Ox.

Линии	Ответ
y = sinx, x = /2, y = 0	2/4 (куб. ед.) или (куб. ед.)
y = √lnx, y = , x = e	 (куб. ед.)
y = lnx, y = , x = e	1

Найти предел – см. «Предел … равен …»

Найти предел на основании свойств пределов – см. «Предел … равен …»

Найти предел, пользуясь правилом Лопиталя – см. «Предел … равен …»

Найти произведение действительного числа на матрицу … – см. «Произведение действительного числа на матрицу … равно …»

Найти произведение матриц – см. «Произведение матриц … равно …»

Найти производную y`_x от функциданной параметрически … при t = …, где t Є [-∞; +∞].

Функция	Точка t =	Ответ
	1	2
	1

Найти производную y`_x от функции, заданной параметрически , где t Є [0; 2п].

(или )

Производная y`_x от функции, заданной параметрически



где u Є [0; 2п], равна …

- ctg2u
Производная y`_x от функции, заданной параметрически



где u Є [0; 2п], равна …

- tgu
Производная y`_x от функции, заданной параметрически



где t Є [0; 2п], равна …

ctg²t
Производная y`_x от функции, заданной параметрически



при t = 1, где t Є [-∞; +∞], равна …

2


Найти разность матриц …

Матрицы	Ответ
−
−
−

Найти ранг матрицы – см. «Ранг матрицы … равен …»

Найти сумму матриц – см. «Сумма матриц … равна …»

Найти третий дифференциал – см. «Третий дифференциал функции»

Наклонной асимптотой графика функции y = x³ / (x² – 3) является

y = x

Несобственный интеграл … равен …

Несобственный интеграл	Ответ
	+ ∞
	0,5 ln2
	1 – ln2
	+ ∞
	-1
	8
	-1
	6
	9

Нормаль к графику функции y = x² в точке M₀(1; 1) определяется уравнением

y = – 1/2 x + 3/2
Нормаль к графику функции y = e^x в точке M₀(0; 1) определяется уравнением

y = – x + 1


Областью определения функции … является:

Функция	Область определения
y = lg|x – 2|	(-∞; 2) U (2; +∞)
y = lg(x + 3)	(-3; +∞)
y = arcsinx	[-1; 1]
	(-∞; 1) U (7; +∞)
	[-4; 4]

Обратная матрица для … – см. «Найти обратную матрицу …»

Объем тела, полученного от вращения плоской фигуры, ограниченной линиями

…,

вокруг оси Ox, равен …

Линии	Объем
y = x2, y = 4	Не отвечать!
y = 3x2 + 6, y = 9	посчитать
y = cosx, y = 0, x = 0, x = /2	1/4  куб. ед.
y = sinx, x = /2, y = 0	2/4 куб. ед.
y = √tgx, y = 0, x = /4	 ln√2 куб. ед.

Определитель … равен …

Определитель	Ответ
	-34
	4
	9
	1
	0
	9
	27
	-3
	-12
	-14
	10
	22
	40
	87
	-36
	0
	80
	48
	4
	20
	4
	-34
	36
	16
	0
	0
	0
	0
	30
	38
	0
	30
	910
	0

Площадь плоской фигуры, ограниченной линиями …, составит …

Площадь плоской фигуры, ограниченной линиями …, составляет …

Линии	Площадь
, x = 0, y = 2, y = 4	ln2 кв. ед.
,	(15/8 – ln4) кв. ед.
,	(15/8 – ln4) кв. ед.
y = x2, x = 1, y = 0	1/3 кв. ед.
y2 = x, y = 4, x = 0	21 1/3 (кв. ед.)
x = y2, y = – x + 2	4,5 (кв. ед.)
x = y2, y = x	1/6 (кв. ед.)
x = y2, x = 4	10 2/3 (кв. ед.)
y = x2 – 9, y = 0	36 кв. ед.
y = x2 – 2x + 1, y = 1	4/3 (кв. ед.)
y = x2 – 4x + 5, y = 5	10 2/3 (кв. ед.)
y = sinx, y = cosx, x = 0, x = п/4	(√2 – 1) (кв. ед.)
y = sinx, x = 0, x = , y = 0	1 (кв. ед.)
x = √y, y = 0, x = 1	1/3 кв. ед.
x = √y + 2, y = 0, x = 6	21 1/3 (кв. ед.)

Пользуясь правилом Лопиталя, можно найти, что предел – см. «Предел … равен …»

Последовательность {-1/n} имеет своим пределом
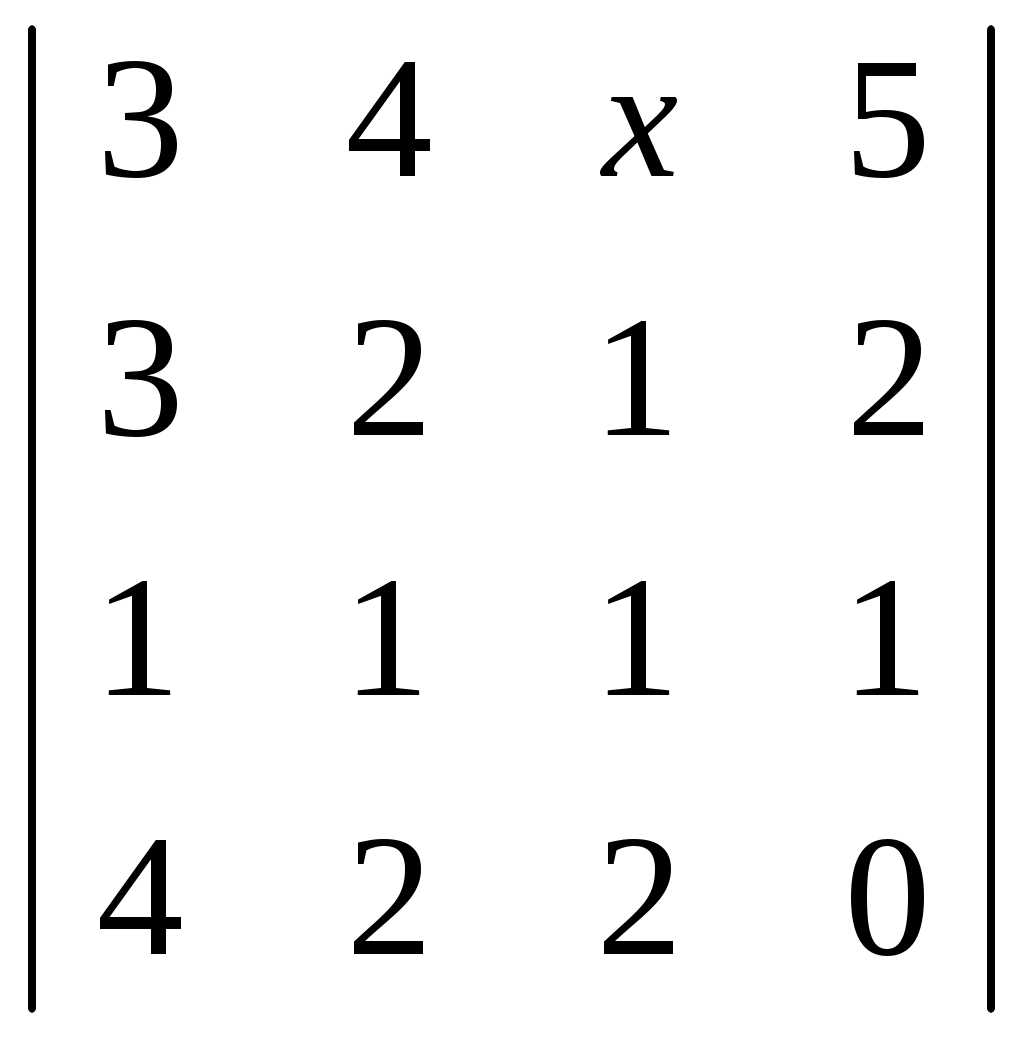
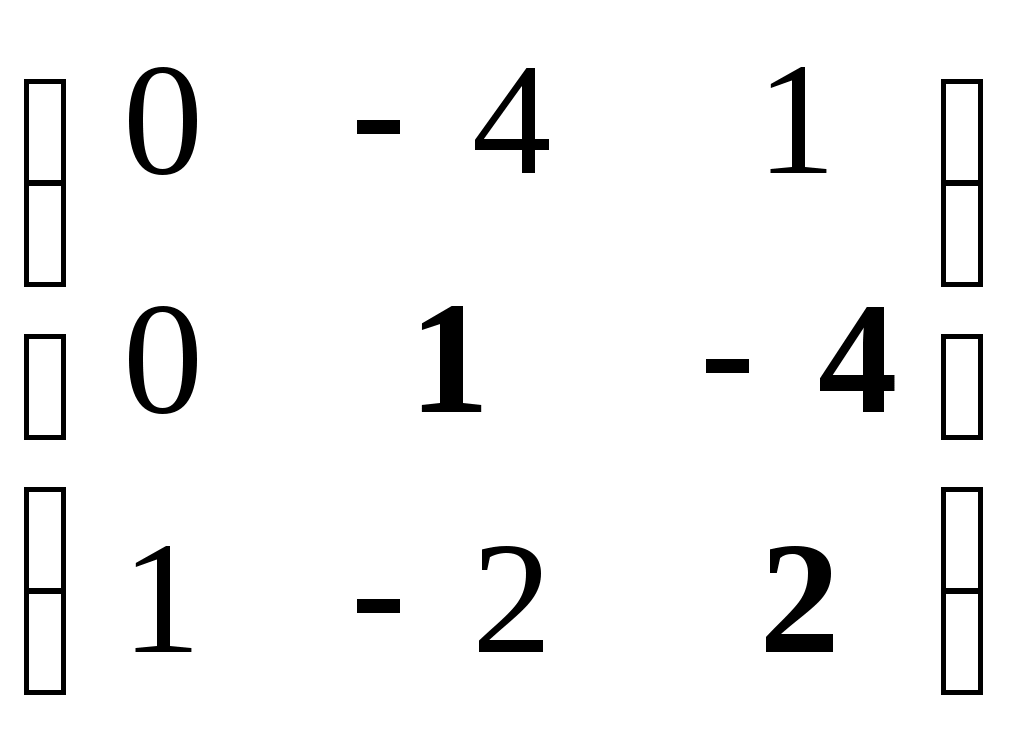