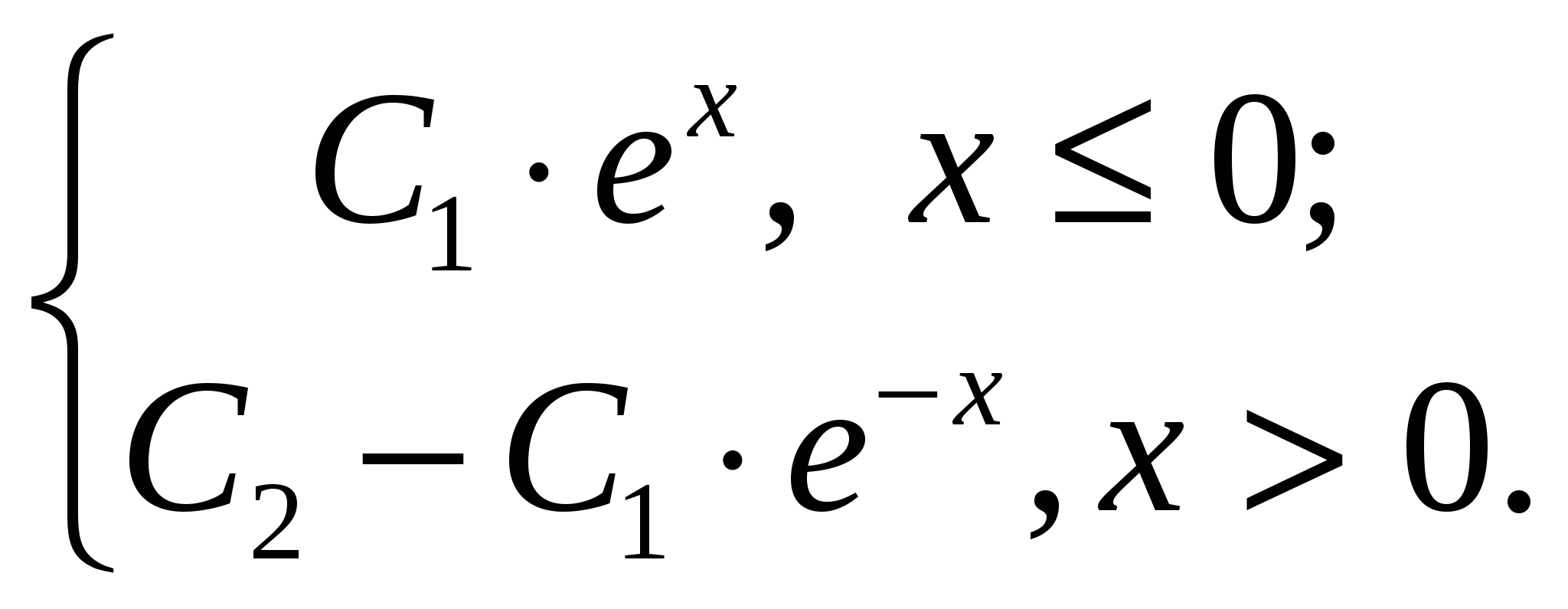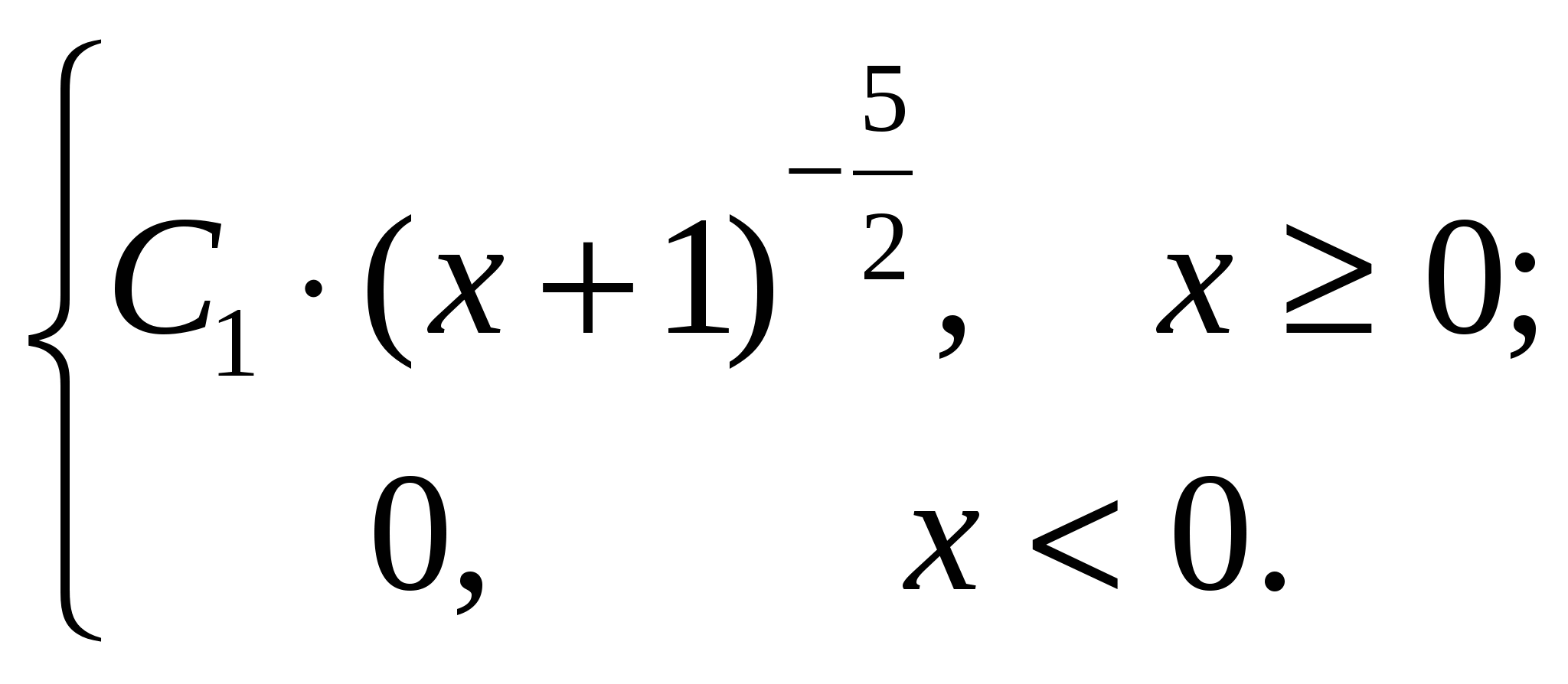|
|
ИДЗ Математика часть 2 ИКРиМ 2 семестр v2. В. Ю. Бодряков Индивидуальные домашние задания (идз) по дисциплине Математика Часть 2 Екатеринбург 2014 Введение Настоящая методическая разработка
6. Два игральных кубика бросаются n = 12 раз с подсчетом сумм выпавших очков. Д.с.в. X – число сумм, кратных четырем.
7. Из ящика, содержащего N = 10 деталей, среди которых n = 6 стандартных деталей, наудачу вынимаются M = 4 детали. Д.с.в. X – число стандартных деталей в выборке.
8. Бросаются два игральных кубика. Д.с.в. X – сумма выпавших очков.
9. На элеватор прибыло N1 = 6 машин агрофирмы АФ-1 и N2 = 9 машин агрофирмы AФ-2. Под разгрузку случайным образом загоняются n = 6 машин. Д.с.в. X – число разгружаемых машин агрофирмы АФ-1.
10. Вероятность того, что стрелок при одном выстреле из пистолета (в обойме n = 9 патронов) попадет в цель равна 0,8. Стрельба ведется до первого промаха. Д.с.в. X – число оставшихся в обойме патронов.
11. Игральный кубик брошен n = 8 раз. Д.с.в. X – число выпадений нечетного числа очков в n бросаниях.
12. В процессе производства изделие высшего качества удается получить только с вероятностью 0,2. С конвейера берутся наугад детали до тех пор, пока не будет взято изделие высшего качества. Д.с.в. X – число проверенных изделий.
13. Бросаются два игральных кубика. Д.с.в. X – модуль разности выпавших очков.
14. Из ящика, содержащего N = 8 деталей, среди которых n = 5 стандартных деталей, наудачу вынимаются m = 3 детали. Д.с.в. X – число стандартных деталей в выборке.
15. Каждая из 5 лампочек имеет дефект с вероятностью 0,1. Дефектная лампочка при включении сразу перегорает и ее заменяют новой. Д.с.в. X – число опробованных ламп.
16. Прибор комплектуется двумя деталями; вероятность брака для первой детали – 0,1, а для второй – 0,05. Для контроля выбрано 4 прибора. Прибор бракуется, если в нем есть хотя бы одна бракованная деталь. Д.с.в. X – число бракованных приборов среди проверенных 4 приборов.
17. Вероятность того, что стрелок при одном выстреле из пистолета (в обойме n = 8 патронов) попадет в цель равна 2/3. Стрельба ведется до первого промаха. Д.с.в. X – число произведенных выстрелов.
18. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Д.с.в. X – число отказавших элементов в одном опыте.
19. В партии из 15 деталей 20% деталей нестандартны. Наудачу отобраны три детали. Д.с.в. X – число нестандартных деталей среди трех отобранных.
20. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,7. Стрелку выдаются патроны до тех пор, пока он не промахнется. Д.с.в. X – число патронов, выданных стрелку.
21. Имеется 6 монет достоинством 10, 5, 5, 2, 1, 1 рублей. Наудачу берутся три монеты. Д.с.в. X – набранная этими монетами сумма.
22. Вероятность того, что лотерейный билет выигрышный, равна 0,1. Покупатель купил 5 билетов. Д.с.в. X – число выигрышей у владельца этих 5 билетов.
23. Два стрелка поражают мишень с вероятностями, соответственно, 0,8 и 0,9 (при одном выстреле), причем первый стрелок выстрелил один раз, а второй – два раза. Д.с.в. X – общее число попаданий в мишень.
24. ОТК должен проверить 12 комплектов, состоящих из 4 изделий каждый, причем каждая деталь может быть стандартной с вероятностью 0,9. Д.с.в. X – число комплектов, состоящих из стандартных деталей.
25. В партии из 15 деталей 40% деталей нестандартны. Наудачу отобраны четыре детали. Д.с.в. X – число стандартных деталей среди четырех отобранных деталей.
26. Три стрелка с вероятностями попадания в цель при отдельном выстреле 0,7, 0,8 и 0,9, соответственно, делают по одному выстрелу. Д.с.в. X – общее число попаданий.
27. Из урны, в которой лежат 2 белых и 8 черных шаров, последовательно вынимают шары до тех пор, пока не появится белый шар. Д.с.в. X – число вынутых при этом шаров.
28. Стрелок поражает мишень с вероятностью 0,7 при одном выстреле. Стрелок стреляет до первого попадания, но делает не более четырех выстрелов. Д.с.в. X – число произведенных выстрелов.
29. Сдача зачета по математической статистике производится до получения положительного результата. Шансы сдать зачет остаются неизменными и составляют 60%. Д.с.в. X – число попыток сдачи зачета.
30. В шестиламповом усилителе перегорела одна лампа. Лампы заменяют новыми одну за другой, пока усилитель не заработает. Д.с.в. X – число замененных ламп.
ИДЗ-11. Закон распределения вероятностей дискретной случайной величины (д.с.в.). Числовые характеристики распределения д.с.в.
Для непрерывной случайной величины (н.с.в.) X задана функция распределения F(x) (плотность функции распределения f(x)). Вычислить соответствующую плотность функции распределения f(x) (функцию распределения F(x)). Проверить выполнение условия нормировки распределений. Построить графики обеих функций. Вычислить числовые характеристики распределений: математическое ожидание M(X) и дисперсию D(X). Вычислить вероятность того, что н.с.в. X примет значения из заданного интервала (a; b).
Примечание: C1, C2 = сonst.
Функция распределения
0 при x < –2,
F(x) = ¼ x + С1 при –2 x < 2,
C2 при 2 x.
Интервал (a; b) = (1; 2).
Плотность функции распределения
0 при x < 1,
f(x) = x + C1 при 1 x < 2,
0 при 2 x.
Интервал (a; b) = (–3/2; 3/2).
Функция распределения
С1 при x < 0,
F(x) = ¼ x + С2arcsin(½x) при 0 x < 2,
1 при 2 x.
Интервал (a; b) = (1; 2).
Плотность функции распределения вероятностей н.с.в. X задана на числовой оси Ox выражением: f(x) = С1exp(–x2). Интервал (a; b) = (–1; 1).
Функция распределения
0 при x < 2,
F(x) = ½ x + C1 при 2 x < 4,
1 при 4 x.
Интервал (a; b) = (–2; 3).
Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С1exp(–(x–1)2/32). Интервал (a; b) = (0; 2).
Плотность функции распределения вероятностей н.с.в. X задана при x 1 выражением: f(x) = exp(1 – С1x); при x < 1 плотность f(x) = 0. Интервал (a; b) = (0; 2).
Н.с.в. задана функцией распределения
0 при x < 0,
F(x) = C1 x2 + C2 при 0 x < 2,
1 при 2 x.
Интервал (a; b) = (¼; ¾).
Плотность функции распределения вероятностей н.с.в. X задана при x 0 выражением: f(x) = С1exp(–3x) (С1 > 0); при x < 0 плотность f(x) = 0. Интервал (a; b) = (0; 2).
Плотность функции распределения вероятностей задана при x [0; ] выражением: f(x) = С1sin2 x; при x [0; ] плотность f(x) = 0. Интервал (a; b) = (¼ ; ¾ ).
Функция распределения задана на всей числовой оси Ox выражением: F(x) = ½ + С1arctg(½x). Интервал (a; b) = (0; 2).
Плотность функции распределения в промежутке (0; ) задана выражением: f(x) = С1sin(½x); вне его – равна нулю. Интервал (a; b) = (0; ¾ ).
Функция распределения
0 при x < 0,
F(x) = C1sin x при 0 x < ½ ,
C2 при ½ x.
Интервал (a; b) = (/6; /3).
Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С1exp(–½(x–1)2). Интервал (a; b) = (–1; 1).
Функция распределения
0 при x < 0,
F(x) = C1cos x + C2 при 0 x < ½ ,
C2 при ½ x.
Интервал (a; b) = (/6; /3).
Функция распределения задана на всей числовой оси Ox выражением: F(x) = ½ + С1arctgx. Интервал (a; b) = (–1; 1).
Плотность функции распределения вероятностей н.с.в. X задана в промежутке (0; 1) выражением: f(x) = С1(x2 + 2x); вне этого промежутка f(x) = 0. Интервал (a; b) = (0; ½).
Плотность функции распределения вероятностей н.с.в. X задана в промежутке (–1; 1) выражением: f(x) = С1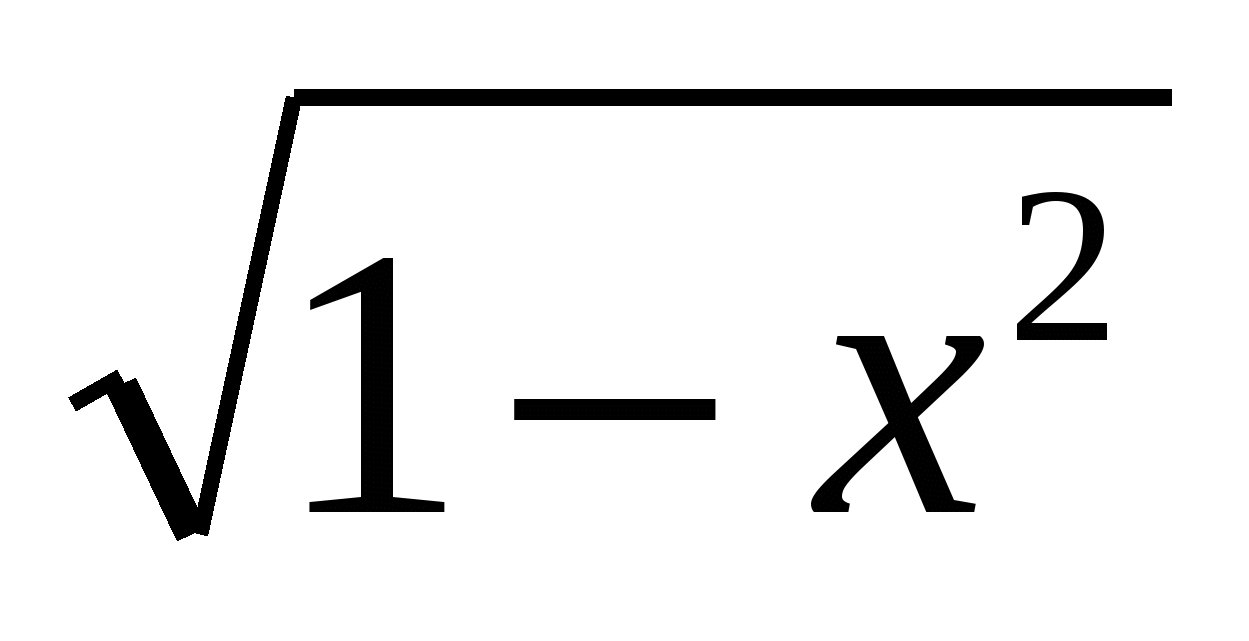 ; вне этого промежутка f(x) = 0. Интервал (a; b) = (0; ½). ; вне этого промежутка f(x) = 0. Интервал (a; b) = (0; ½).
Н.с.в. X равномерно распределена в промежутке (1; 4). Вне этого промежутка f(x) = 0. Интервал (a; b) = (1; 3).
Функция распределения вероятностей н.с.в. X задана при x 0 выражением: F(x) = С1 – exp(–С1x). Интервал (a; b) = (2; +).
Плотность функции распределения вероятностей н.с.в. X задана на числовой оси Ox выражением: f(x) = С1e–|x|. Интервал (a; b) = (–2; 2).
Плотность функции распределения вероятностей н.с.в. X задана в промежутке (–2; 2) выражением: f(x) = С1/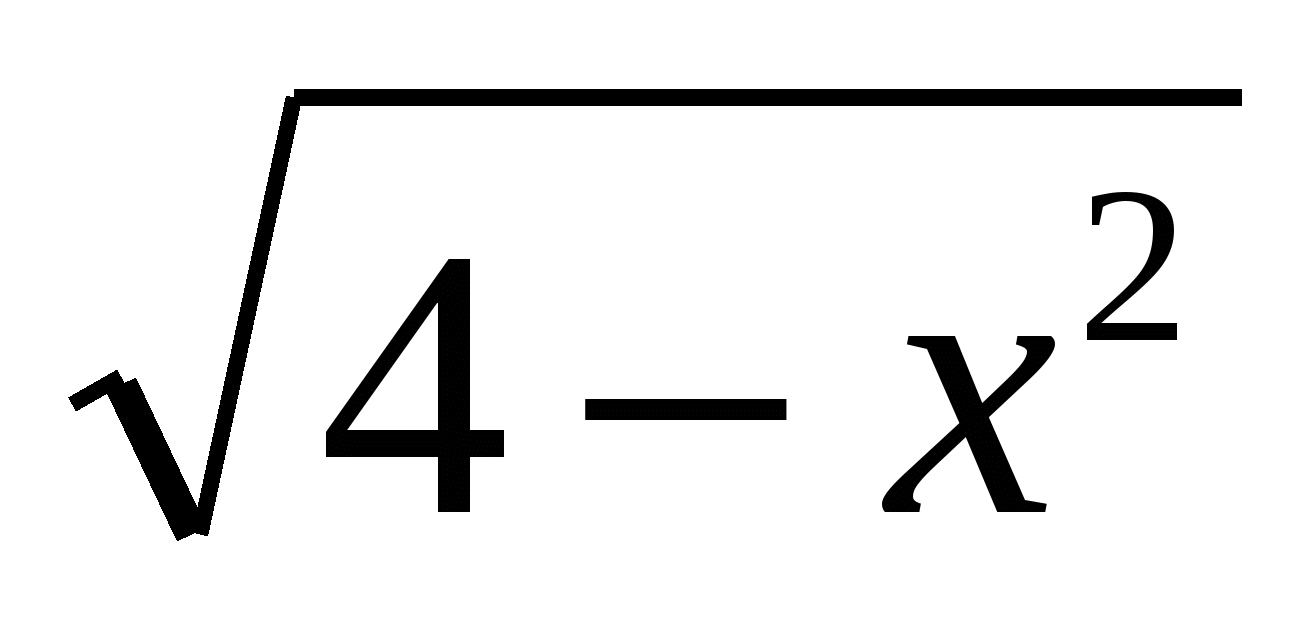 ; вне этого промежутка f(x) = 0. Интервал (a; b) = (1; +). ; вне этого промежутка f(x) = 0. Интервал (a; b) = (1; +).
Н.с.в. X равномерно распределена в промежутке (–1; 3). Вне этого промежутка f(x) = 0. Интервал (a; b) определяется неравенством |x - 1| < 1.
Плотность функции распределения вероятностей н.с.в. X задана при x 0 выражением: f(x) = С1exp(–2x); при x < 0 плотность распределения f(x) = 0. Интервал (a; b) = (0; 2).
Н.с.в. задана функцией распределения
F(x) = 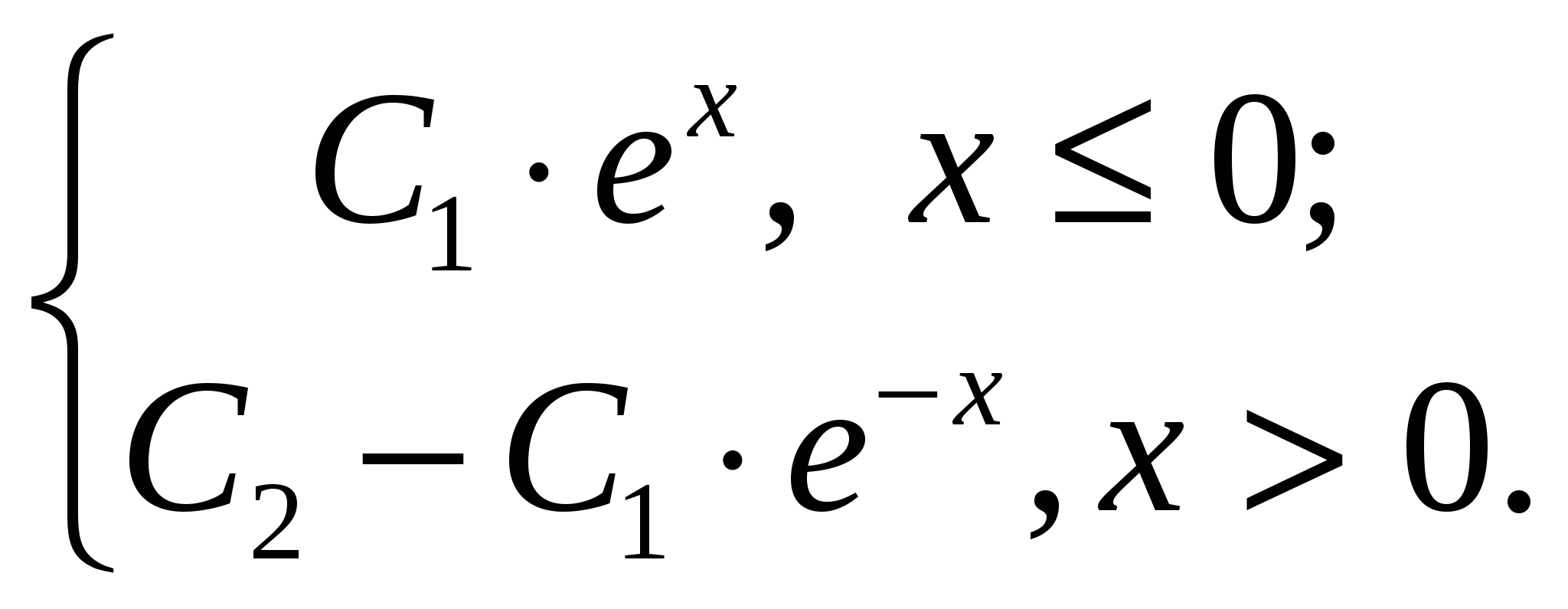
Интервал (a; b) = (–1; 3).
Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С1exp(–(x–4)2/50). Интервал (a; b) = (0; 4).
Плотность функции распределения
f(x) = 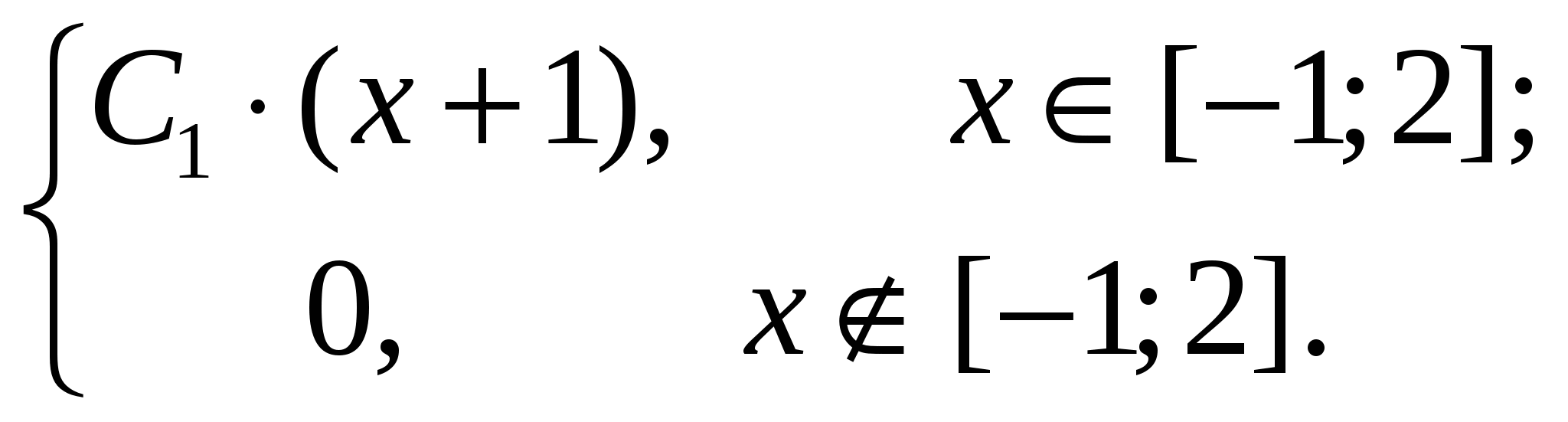
Интервал (a; b) определяется неравенством |x| < 1.
Плотность функции распределения на числовой оси: f(x) = С1 + 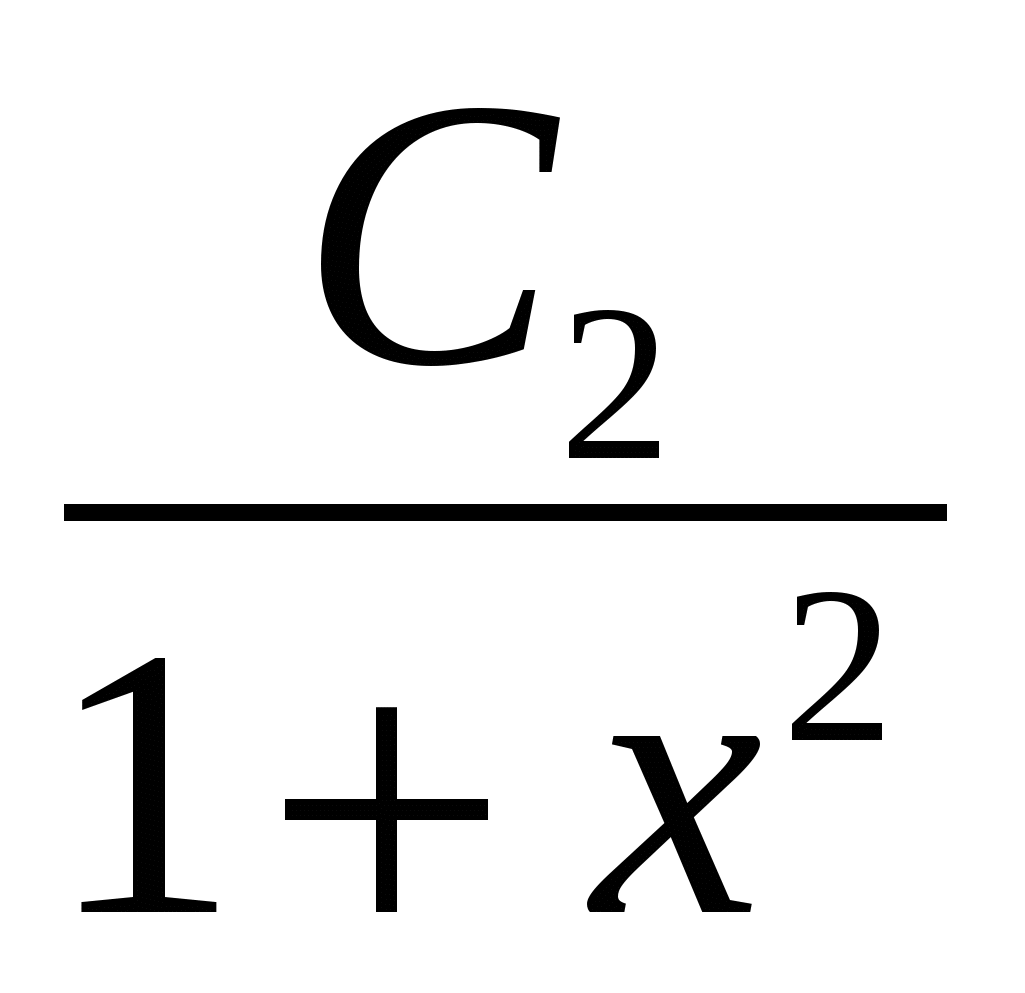 (распределение Коши). Интервал (a; b) = (1; +). (распределение Коши). Интервал (a; b) = (1; +).
Плотность функции распределения
f(x) = 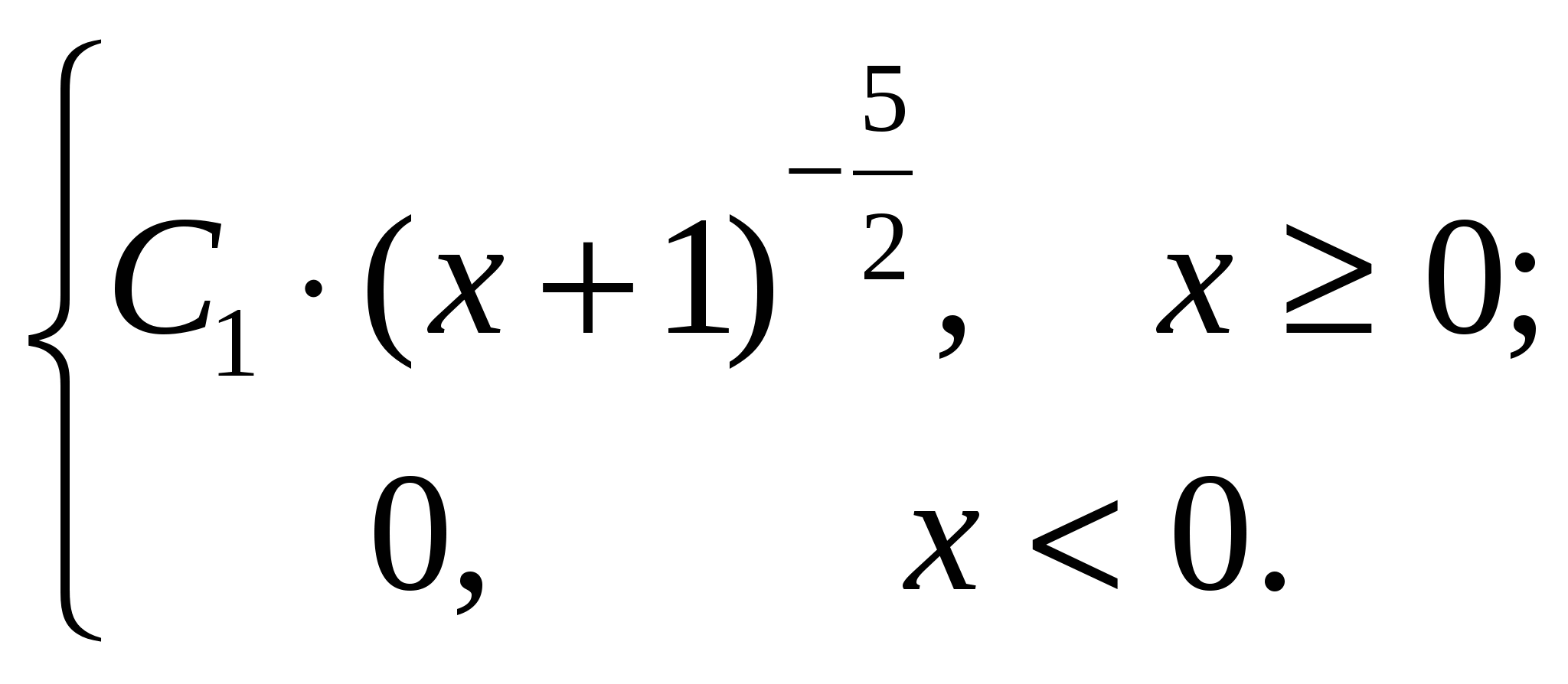
Интервал (a; b) определяется неравенством |x – ⅓| < 1.
Н.с.в. задана функцией распределения
0 при x < 0,
F(x) = C1x – x2 при 0 x < 1,
1 при 1 x.
Интервал (a; b) = (–⅓; ⅓).
ИДЗ-12. Статистическое распределение случайной величины и его числовые характеристики.
Представлены статистические данные. Требуется: 1) составить дискретный вариационный ряд, при необходимости упорядочив его; 2) определить основные числовые характеристики ряда; 3) дать графическое представление ряда в виде полигона (гистограммы) распределения; 4) сформулировать содержательные выводы.
Прим. 1) При проверке статистической гипотезы о виде распределения принять уровень значимости = 0,05; 2) Для числовой обработки данных рекомендуется использовать подходящий математический пакет, например, электронную таблицу MS Excel.
Увлеченный статистической наукой студент путем опроса получил исходные («сырые») статистические данные по росту и весу 20 своих одногруппников:
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Рост, см
|
160
|
168
|
175
|
169
|
170
|
169
|
162
|
166
|
163
|
160
|
Вес, кг
|
48
|
58
|
69
|
64
|
69
|
70
|
51
|
60
|
67
|
54
|
№ п/п
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Рост, см
|
158
|
173
|
162
|
173
|
156
|
158
|
168
|
170
|
162
|
155
|
Вес, кг
|
48
|
58
|
44
|
50
|
56
|
56
|
51
|
50
|
60
|
50
|
После упорядочения вариационного ряда требуется изучить распределение студентов по росту.
Результаты контрольных измерений веса пирожных в кафе приведены в таблице:
Вес, г
|
20,0
|
20,2
|
20,4
|
20,6
|
20,8
|
21,0
|
21,2
|
21,4
|
21,6
|
21,8
|
22,0
|
Кол-во пирожных
|
2
|
3
|
7
|
11
|
17
|
20
|
16
|
13
|
6
|
4
|
1
|
Помимо основного задания требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Имеются следующие данные о размере семьи работников цеха (число человек в семье):
3 4 5 2 3 6 4 2 5 3 4 2 7 3 3 6
2 3 8 5 6 7 3 4 5 4 3 3 4.
Хронометраж операций пайки радиаторов на ремонтном предприятии дал следующие результаты:
Время пайки, мин.
|
20 – 30
|
30 – 40
|
40 – 50
|
50 – 60
|
60 – 70
|
Итого
|
Кол-во радиаторов
|
2
|
5
|
10
|
17
|
1
|
35
|
Имеются следующие данные о возрастном составе группы студентов вечернего отделения:
18 38 28 29 26 38 34 22 28 30
22 23 35 33 27 24 30 32 28 25
29 26 31 24 29 27 32 25 29 20.
По предприятию получены данные о расстоянии перевозки партий груза в международном сообщении (км) за некоторый период:
560 1060 420 1410 1500 400 3800 700 1780 450
449 285 1850 2200 800 1200 1540 1150 180 452
452 2500 300 400 900 1800 452 1850 1225 220
1800 300 920 1400 1400 480 850 200 400 1440
420 1700 1615 3500 300 320 600 965 450 245.
Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:
Группы магазинов по товарообороту, млн. руб.
|
40– 50
|
50– 60
|
60– 70
|
70– 80
|
80– 90
|
90– 100
|
100– 110
|
110– 120
|
120– 130
|
130– 140
|
Число магазинов
|
2
|
4
|
7
|
10
|
15
|
20
|
22
|
11
|
6
|
3
|
На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1;4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5.
По автотранспортному предприятию, осуществляющему перевозку грузов автомобилями КамАЗ-5320 грузоподъемностью 16 т, имеются следующие данные о весе партий груза (т):
8 11 14 6 10 13 12 16 15 16
16 10 16 13 14 16 16 4 16 14
5 13 11 2 16 8 16 7 14 16.
В результате метеонаблюдений получено статистическое распределение дневных температур в июне месяце:
Температура, С
|
20º
|
23º
|
24º
|
26º
|
27º
|
30º
|
Число дней
|
1
|
4
|
5
|
8
|
10
|
2
|
Получены данные об урожайности ржи на различных участках поля:
Урожайность
ржи, ц/га
|
9 – 12
|
12 – 15
|
15 – 18
|
18 – 21
|
21 – 24
|
24 – 27
|
Доля участка в общей площади, %
|
6
|
12
|
33
|
22
|
19
|
8
|
Имеются следующие данные о часовой интенсивности движения автомобилей на автомагистрали (авт./час):
140 99 80 140 218 218 340 92 152 120 130
50 110 130 96 48 48 36 60 30 86 102
90 210 220 261 261 282 312 68 80 131 190.
Известно распределение золотых медалистов, окончивших в 2001 году школы Ярославской области, по районам:
Кол-во золотых медалистов
|
0
|
1
|
3
|
4
|
6
|
8
|
20
|
Кол-во районов
|
6
|
1
|
4
|
2
|
1
|
3
|
1
|
Имеются следующие данные о количестве заявок на автомобили технической помощи по дням:
11 2 5 14 7 2 8 10 2 6
10 8 3 13 11 8 8 2 9 8
5 14 4 10 12 6 8 2 8 7
9 2 8 4 6 13 5 3 12 2
2 7 9 8 5 8 6 10 11 5.
Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Обработка детали №37 производится в цехе на токарном полуавтомате. На 25 января получены следующие данные о размере обработанных деталей (в отклонениях от номинала):
Отклонения от номинала (в сотых долях мм)
|
0 – 2
|
2 – 4
|
4 – 6
|
6 – 8
|
8 – 10
|
10 – 12
|
12 – 14
|
Число деталей
|
6
|
15
|
18
|
36
|
30
|
9
|
6
|
Для характеристики технологического процесса, помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Имеются следующие данные о величине межремонтного пробега автомобилей ЗИЛ-133:
Величина межремонтного пробега, тыс. км
|
80 - 100
|
100 - 120
|
120 - 140
|
140 - 160
|
160 - 180
|
Число автомобилей
|
10
|
60
|
100
|
26
|
14
|
Для организации технологического процесса ремонта автомобилей, помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Распределение рабочих предприятия по размеру месячного дохода следующее:
Месячный доход, руб.
|
4200 - 4500
|
4500 - 4800
|
4800 - 5100
|
5100 - 5400
|
5400 и более
|
Итого
|
Число рабочих
|
75
|
218
|
300
|
201
|
25
|
819
|
Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Имеются данные наблюдения над числом посетителей сайта академии в течение 40 дней: 72, 76, 101, 123, 74, 64, 111, 122, 74, 68, 65, 107, 65, 119, 71, 77, 67, 104, 108, 128, 72, 85, 80, 123, 65, 90, 76, 84, 105, 104, 122, 128, 107, 86, 79, 80, 87, 109, 107, 94.
Распределение промышленных предприятий города по численности работников следующее:
Группы предприятий по численности работников, чел
|
До 50
|
50 - 100
|
100 - 200
|
200 - 400
|
400 - 800
|
800 - 1200
|
1200 и более
|
Число предприятий
|
140
|
80
|
35
|
60
|
45
|
12
|
10
|
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Измерение роста 100 студентов – первокурсников университета дало следующие результаты:
Рост, см
|
154-158
|
158-162
|
162-166
|
166-170
|
170-174
|
174-178
|
178-182
|
Число студентов
|
10
|
14
|
26
|
28
|
12
|
8
|
2
|
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
В опытах по рассеянию -частиц на мишени получены данные по числу -частиц, достигших счетчика в указанном секторе:
№ сектора
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
Кол-во -частиц
|
6
|
21
|
81
|
156
|
200
|
195
|
152
|
97
|
54
|
26
|
11
|
7
|
Распределение рабочих цеха по проценту выполнения норм выработки выглядит следующим образом:
% выполнения норм
|
50-70
|
70-90
|
90-110
|
110-130
|
130-150
|
150-170
|
Число рабочих
|
20
|
25
|
35
|
30
|
20
|
10
|
Выполняет ли производственный план цех в целом?
Для определения «общего интеллекта» школьникам предлагалось раскрыть геометрические закономерности. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
Кол-во баллов
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Кол-во школьников
|
4
|
11
|
15
|
16
|
19
|
15
|
5
|
Тренер по легкой атлетике должен решить, кого из двух спортсменов выбрать для стометровой дистанции в предстоящих соревнованиях. Тренер свое решение должен принять на основании пяти забегов между атлетами:
Анна (сек.)
|
12,1
|
12,0
|
12,0
|
16,8
|
12,1
|
Ирина (сек.)
|
12,3
|
12,4
|
12,4
|
12,5
|
12,4
|
а) Основываясь на этих данных, кого из атлетов следует выбрать тренеру и почему? б) Если тренер знал о падении Анны на старте в четвертом забеге, то следует ли учесть это?
Предположим, что вследствие ошибки данные, содержащие сведения о среднемесячной заработной плате продавцов (тыс. руб.) в девяти торговых компаниях, имеют вид:
13, 15, 14, 17, 13, 16, 15, 16, 61.
Показать, как эта ошибка влияет на числовые характеристики вариационного ряда. Каковы истинные (скорректированные) характеристики ряда?
Увлеченный статистической наукой студент путем опроса получил исходные («сырые») статистические данные по росту и весу 20 своих одногруппников:
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Рост, см
|
160
|
168
|
175
|
169
|
170
|
169
|
162
|
166
|
163
|
160
|
Вес, кг
|
48
|
58
|
69
|
64
|
69
|
70
|
51
|
60
|
67
|
54
|
№ п/п
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Рост, см
|
158
|
173
|
162
|
173
|
156
|
158
|
168
|
170
|
162
|
155
|
Вес, кг
|
48
|
58
|
44
|
50
|
56
|
56
|
51
|
50
|
60
|
50
|
После упорядочения вариационного ряда требуется изучить распределение студентов по весу.
На основе данных анализа эффективности работы 50-и предприятий города по изменению реальной заработной платы на них в отчетном году (в % к предыдущему году), получен следующий статистический ряд:
-
№
|
Эр[%]
|
№
|
Эр[%]
|
№
|
Эр[%]
|
№
|
Эр[%]
|
№
|
Эр[%]
|
1
|
91
|
11
|
100
|
21
|
102
|
31
|
104
|
41
|
108
|
2
|
93
|
12
|
100
|
22
|
102
|
32
|
104
|
42
|
109
|
3
|
95
|
13
|
101
|
23
|
103
|
33
|
105
|
43
|
109
|
4
|
96
|
14
|
101
|
24
|
103
|
34
|
105
|
44
|
110
|
5
|
97
|
15
|
101
|
25
|
103
|
35
|
106
|
45
|
111
|
6
|
97
|
16
|
101
|
26
|
103
|
36
|
106
|
46
|
112
|
7
|
97
|
17
|
101
|
27
|
103
|
37
|
106
|
47
|
113
|
8
|
97
|
18
|
102
|
28
|
103
|
38
|
107
|
48
|
103
|
9
|
98
|
19
|
102
|
29
|
104
|
39
|
107
|
49
|
108
|
10
|
98
|
20
|
102
|
30
|
104
|
40
|
107
|
50
|
98
|
Имеются опытные данные о числе звонков в службу аварийной помощи в течение рабочего дня:
-
Интервалы
(часы смены)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Число звонков
|
16
|
27
|
17
|
15
|
24
|
19
|
11
|
15
|
Требуется построить теоретическую кривую равномерного распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Имеются результаты опроса группы молодёжи, состоящей из 200 человек, о возрасте первого употреблении наркотиков. Результаты представлены в виде интервального вариационного ряда:
Интервалы возрастов, лет
|
11 - 12
|
12 - 13
|
13 - 14
|
14 - 15
|
15 - 16
|
16 - 17
|
17 - 18
|
18 - 19
|
19 - 20
|
20 - 21
|
Объем группы, чел.
|
7
|
12
|
14
|
25
|
48
|
42
|
24
|
13
|
10
|
5
|
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города Ярославля представлены в сгруппированном виде:
Длительность оборота, дни
|
24 - 32
|
32 - 40
|
40 - 48
|
48 - 56
|
56 - 64
|
64 - 72
|
72 - 80
|
Кол-во предприятий
|
2
|
4
|
10
|
15
|
11
|
5
|
3
|
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Литература
Андерсон Дж.А. Дискретная математика и комбинаторика.: Пер. с англ. М.: Изд. Дом «Вильямс», 2004. – 960 с.
Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшее образование, 2006. – 404 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшее образование, 2006. – 404 с.
Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: учеб. пособие. М.: Финансы и статистики, 2004. – 336 с.
|
|
|
 Скачать 0.67 Mb.
Скачать 0.67 Mb.