ИДЗ Математика часть 2 ИКРиМ 2 семестр v2. В. Ю. Бодряков Индивидуальные домашние задания (идз) по дисциплине Математика Часть 2 Екатеринбург 2014 Введение Настоящая методическая разработка

• Название: В. Ю. Бодряков Индивидуальные домашние задания (идз) по дисциплине Математика Часть 2 Екатеринбург 2014 Введение Настоящая методическая разработка
• Анкор: ИДЗ Математика часть 2 ИКРиМ 2 семестр v2.doc
• Дата: 10.03.2018
• Размер: 0.67 Mb.
• Имя файла: ИДЗ Математика часть 2 ИКРиМ 2 семестр v2.doc
• Тип: Методическая разработка; #16480
• страница: 2 из 5

ИДЗ-9. Формулы Муавра – Лапласа. Вероятности редких событий.

Решите задачу на вычисление вероятностей случайных событий с применением локальной или интегральной теорем Муавра – Лапласа или распределения Пуассона.

При рождении одного ребенка вероятность появления мальчика равна 0,51. Какой объем выборки новорожденных следует взять, чтобы с вероятностью 95% удостовериться в справедливости данного вывода? Допустимая ошибка  1% от объема выборки.

Решение: Введем обозначения: p = 0,51 – вероятность рождения мальчика; q = 0,49 – вероятность рождения девочки (т.е. нерождения мальчика); n – искомый объем выборки.

Пусть в выборке новорожденных объема n имеется k мальчиков. Для того, чтобы относительная эмпирическая частота отклонялась от вероятности p не более, чем на  0,01, число мальчиков должно быть заключено в пределах k₁  k  k₂, где k₁ = np – 0,01n, k₂ = np + 0,01n.

Согласно интегральной теореме Муавра – Лапласа вероятность того, что k₁  k  k₂, может быть найдена по формуле:

P(k₁  k  k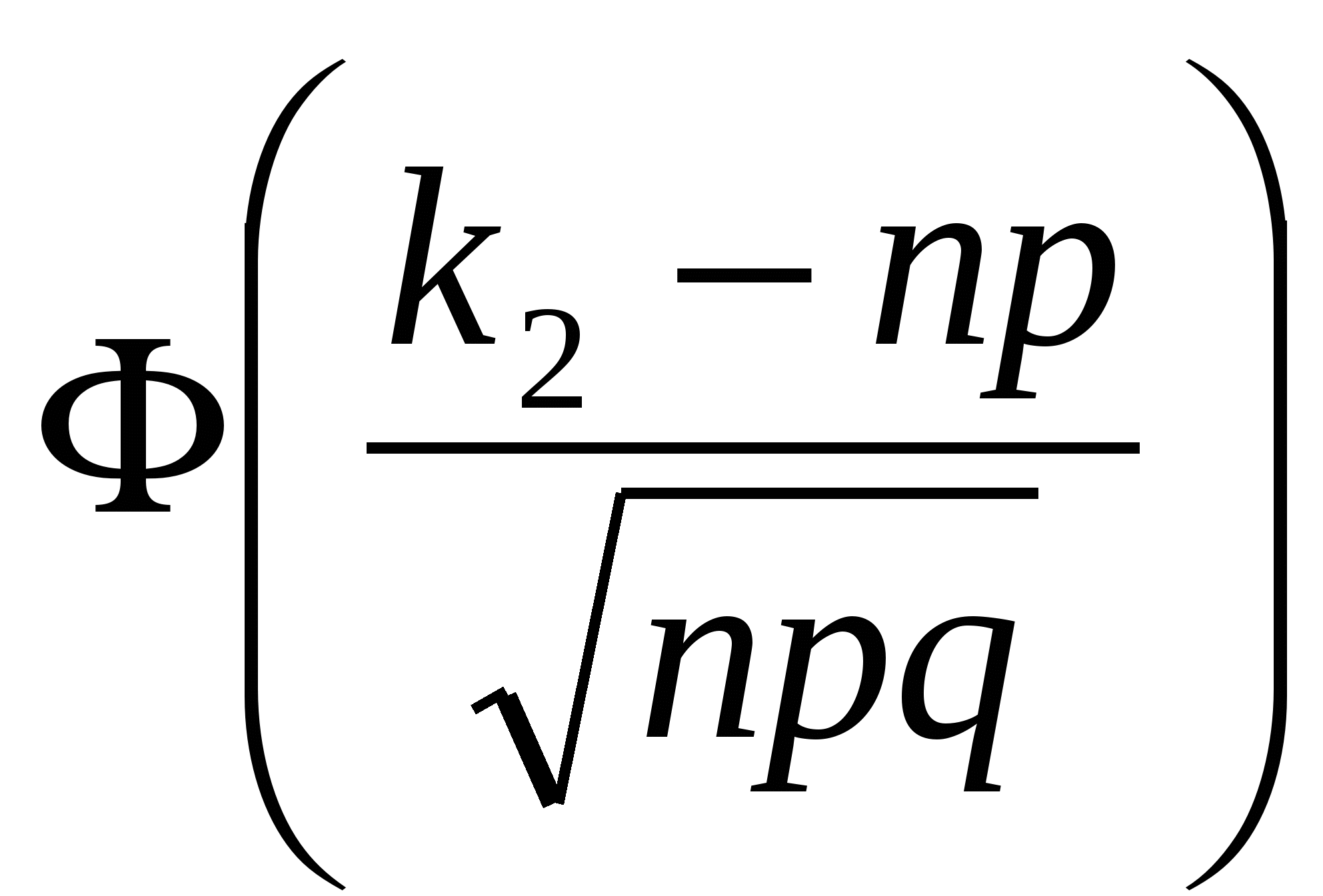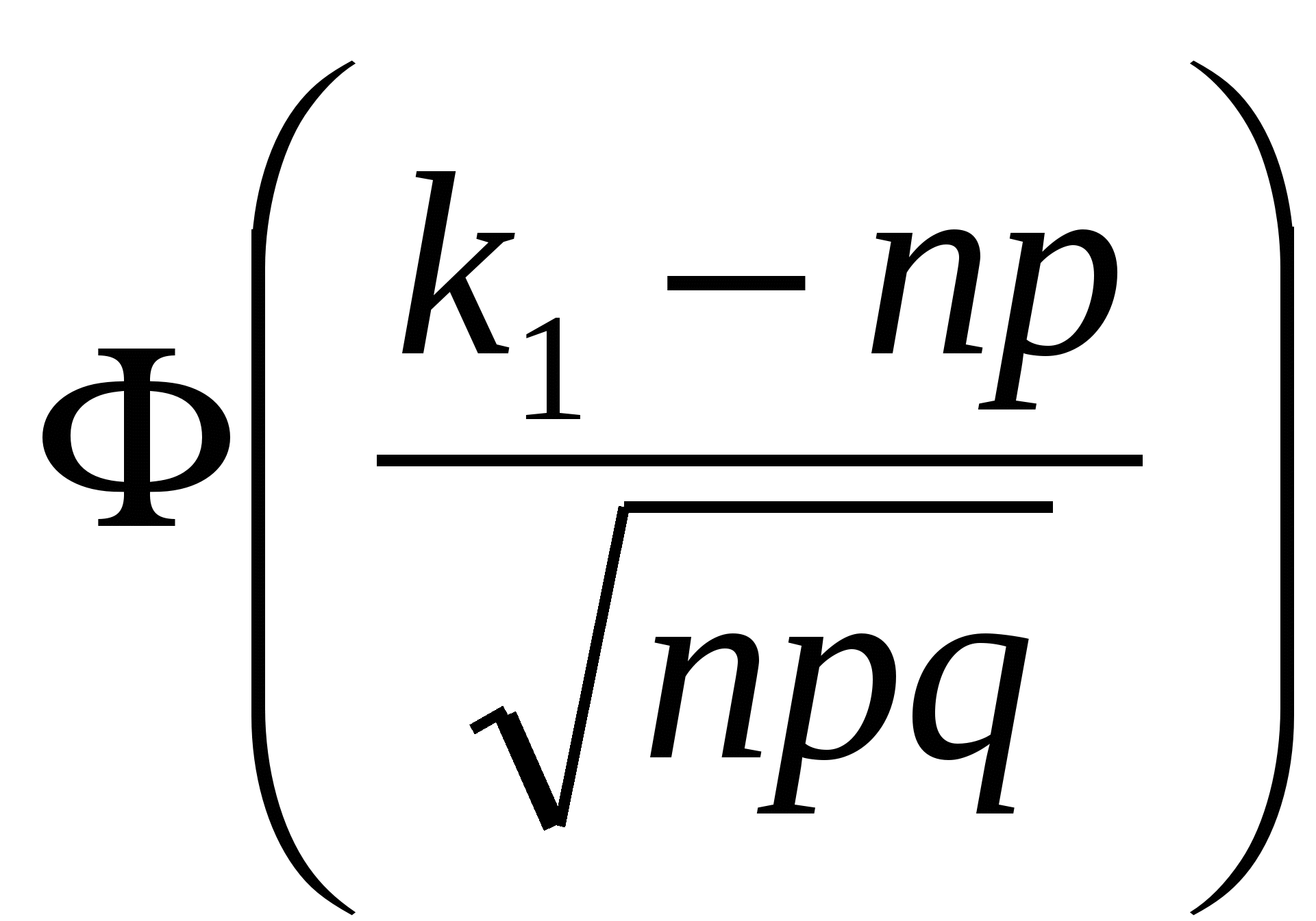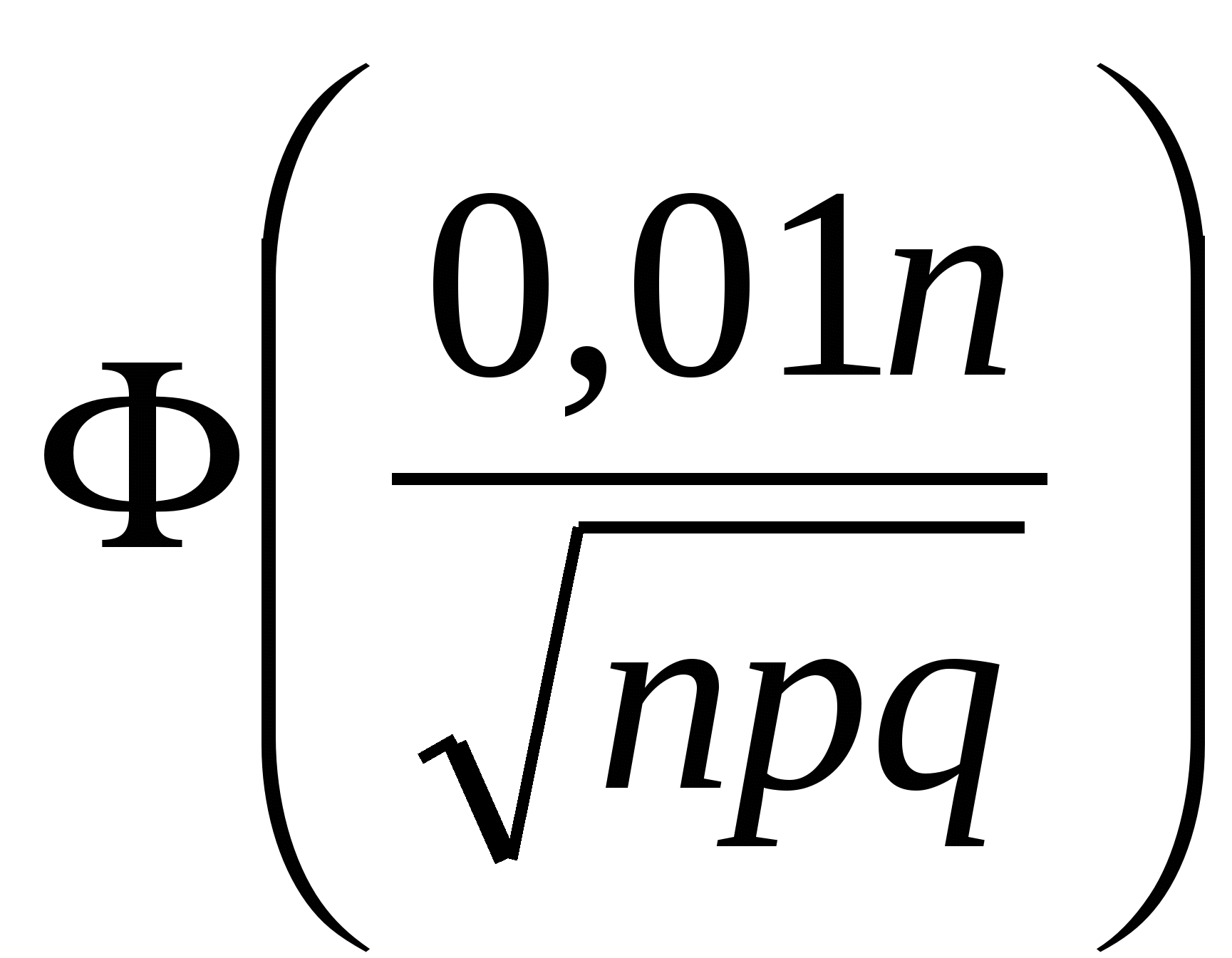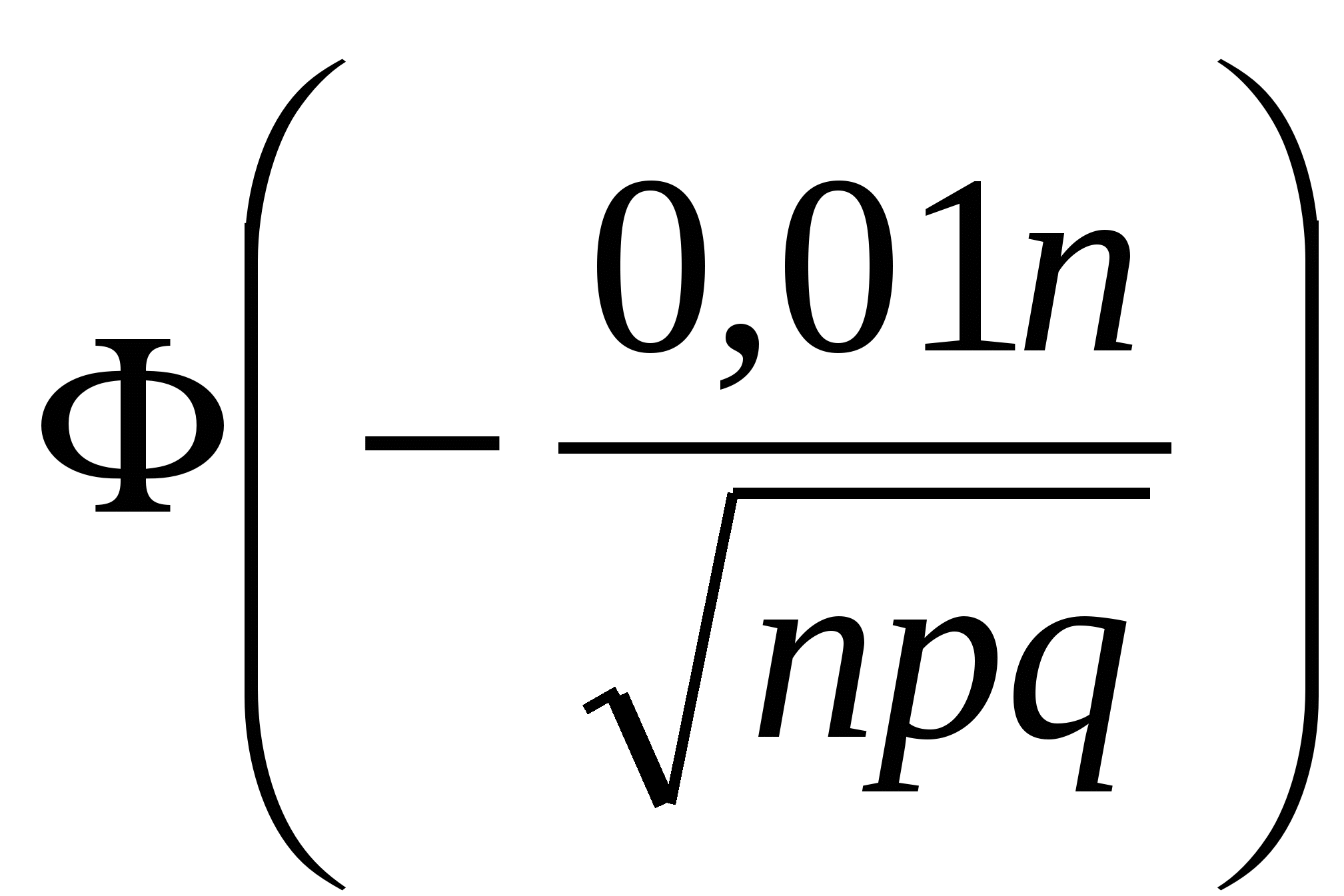₂) = –= –= 2.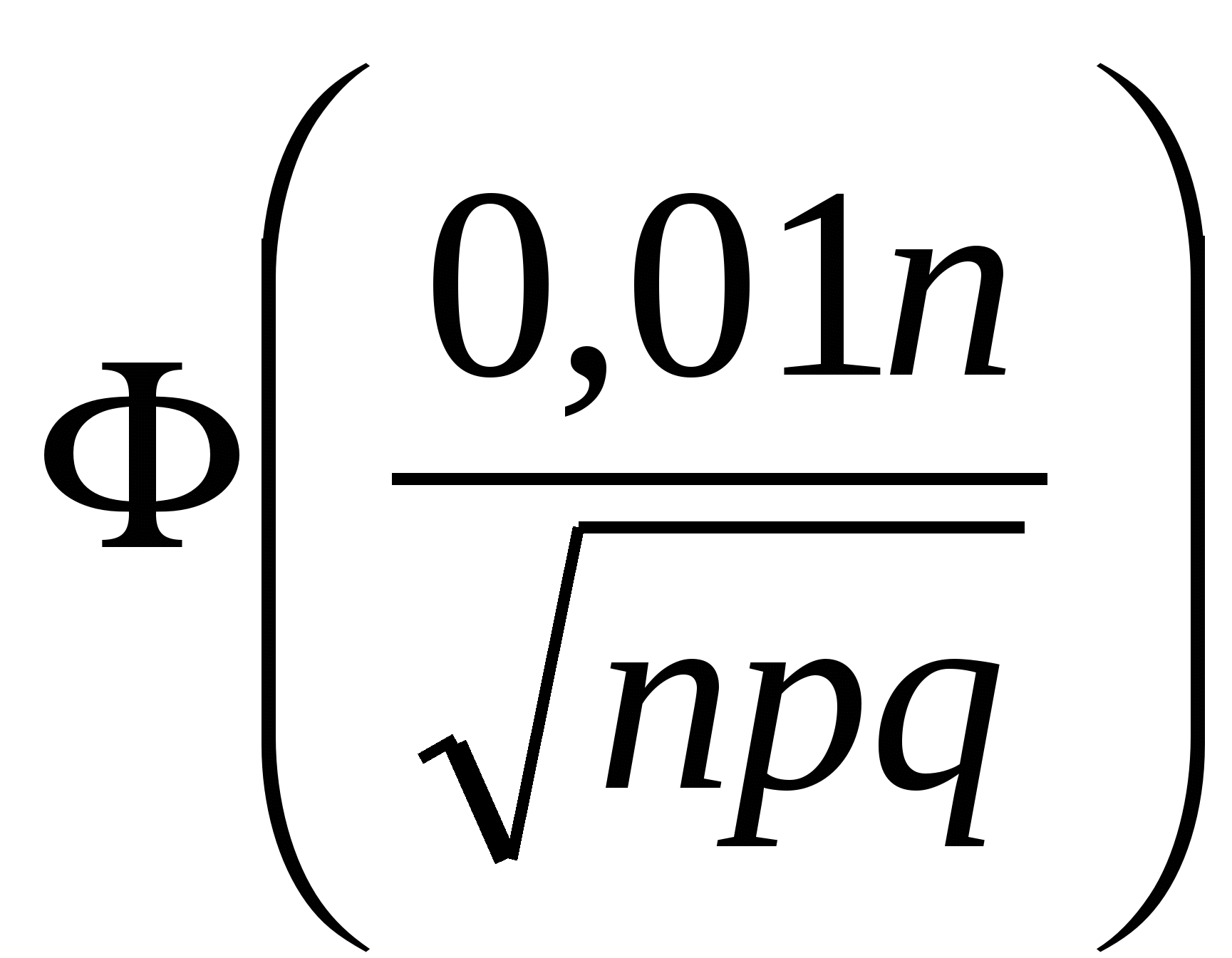

Здесь (z) – табулированная функция Лапласа; учтена также нечетность функции Лапласа: (–z) = –(z).

По условию задачи

P(k₁  k  k₂) = 2 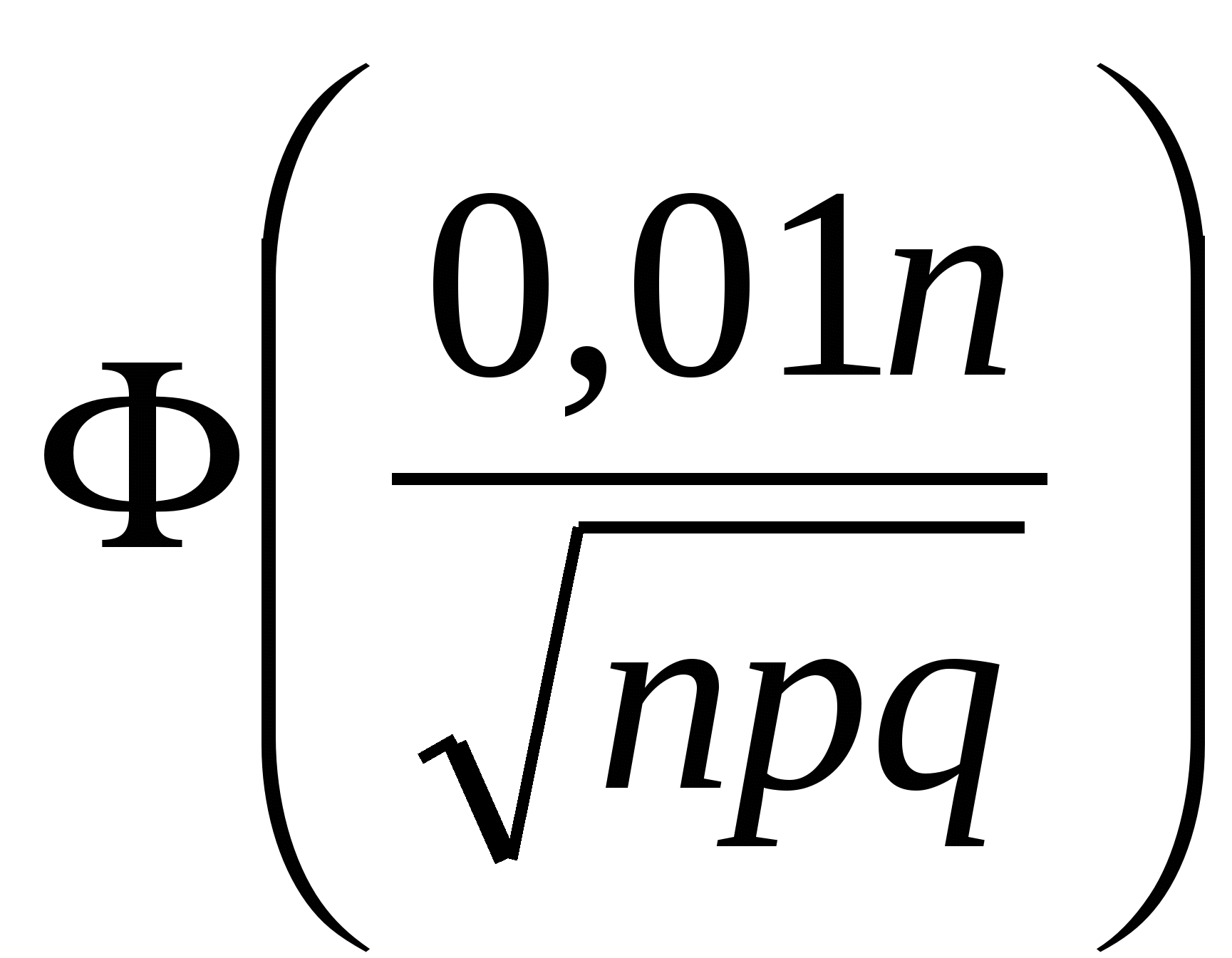= 0,95,

Откуда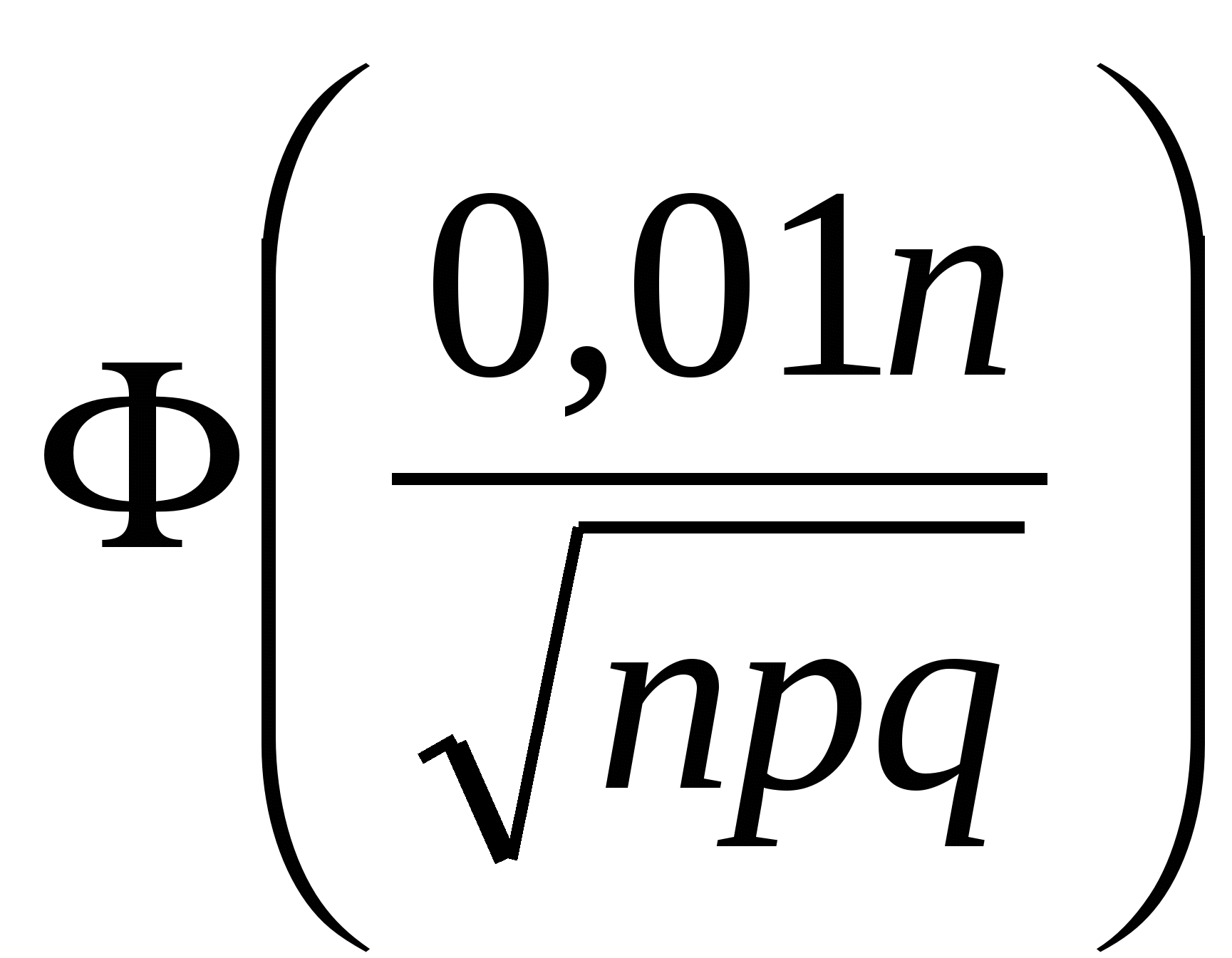

 = 0,475.

Далее, по таблице значений функции Лапласа находим

0,02 = 1,96,

откуда, окончательно, n = 9604.

Ответ: Следует взять выборку новорожденных объемом не менее n = 9604 чел.
ИДЗ-10. Закон распределения вероятностей дискретной случайной величины (д.с.в.). Числовые характеристики распределения д.с.в.

Составьте закон распределения вероятностей дискретной случайной величины (д.с.в.) X – числа k выпадений хотя бы одной «шестерки» в n = 8 бросаниях пары игральных кубиков. Постройте многоугольник распределения. Найдите числовые характеристики распределения (моду распределения, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение (X)).

Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз». Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу».

Поскольку вероятность непоявления «шестерки» при бросании одного кубика равна 5/6, то по теореме умножения вероятностей

P(Ā) = q = = .

Соответственно,

P(A) = p = 1 – P(Ā) = .

Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X – число k выпадений хотя одной шестерки при бросании двух кубиков подчиняется биномиальному закону распределения вероятностей:

P_n(k) = pⁿq^n–k,

где = – число сочетаний из n по k. Проведенные для данной задачи расчеты удобно оформить в виде таблицы (табл. 2):
Таблица 2

Распределение вероятностей д.с.в. X  k (n = 8; p = ; q = )

k	0	1	2	3	4	5	6	7	8	
	1	8	28	56	70	56	28	8	1
Pn(k)	0,0541	0,1904	0,2932	0,258	0,1419	0,05	0,011	0,0013	0,0001	1

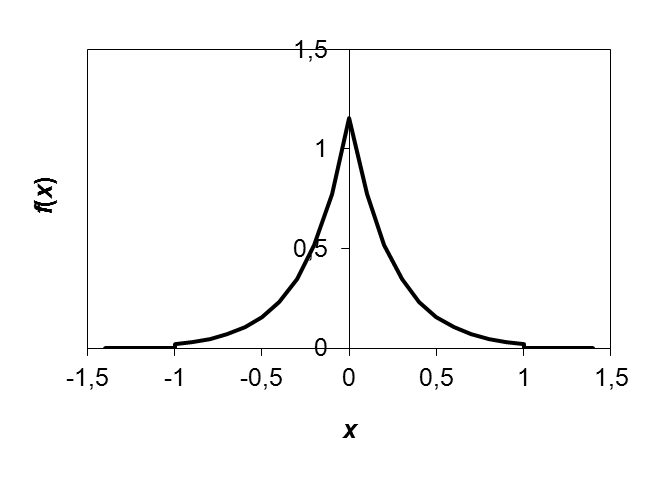
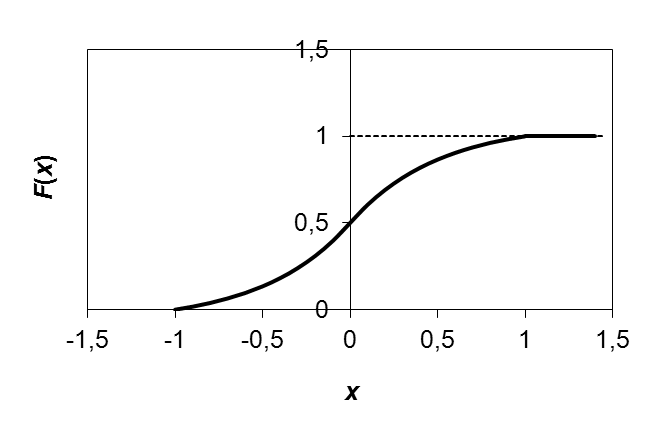
Полигон (многоугольник) распределения вероятностей дискретной случайной величины X представлен на рис. 2: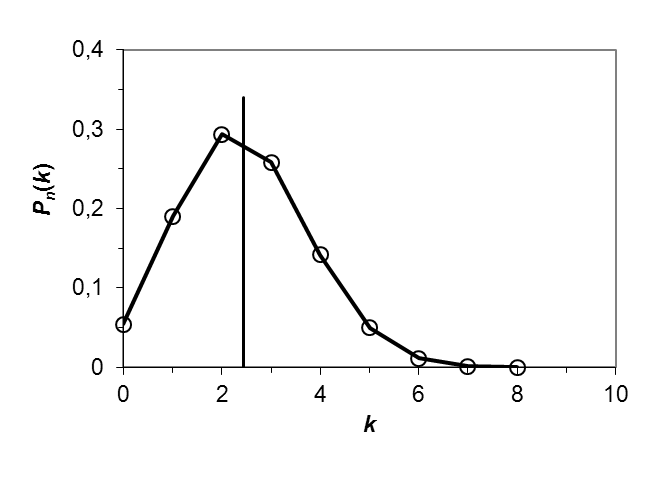


Рис. 2. Полигон распределения вероятностей д.с.в. X=k. Вертикальной линией показано математическое ожидание распределения M(X).

Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P₈(2) = 0,2932 максимально). Математическое ожидание по определению равно:

M(X) = = 2,4444,

где x_k = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:

D(X) = = 4,8097.

Среднее квадратическое отклонение (СКО):

(X) = = 2,1931.

Для наглядности математическое ожидание M(X) д.с.в. X, характеризующее «центр тяжести» распределения, показано на рис. 2 вертикальной сплошной линией.

Ответ: Полигон распределения показан на рис. 2. Мода распределения равна 2; математическое ожидание M(X) = 2,4444; дисперсия D(X) = 4,8097; СКО (X) = 2,1931.
ИДЗ-11. Закон распределения вероятностей непрерывной случайной величины (н.с.в.). Числовые характеристики распределения н.с.в.

Для непрерывной случайной величины (н.с.в.) X задана плотность функции распределения: f(x) = С₁exp(–2|x|) при |x|  1; при |x| > 1 f(x) = 0. Нормируйте плотность распределения. Вычислите функцию распределения F(x). Постройте графики обеих функций. Вычислите числовые характеристики распределений: математическое ожидание M(X), дисперсию D(X), СКО (X). Вычислите вероятность того, что н.с.в. X примет значения из заданного интервала (a; b) = (1/2; 3/2).

Решение: Прежде всего, нормируем на единицу плотность функции распределения f(x); отсюда определится неизвестная постоянная С₁: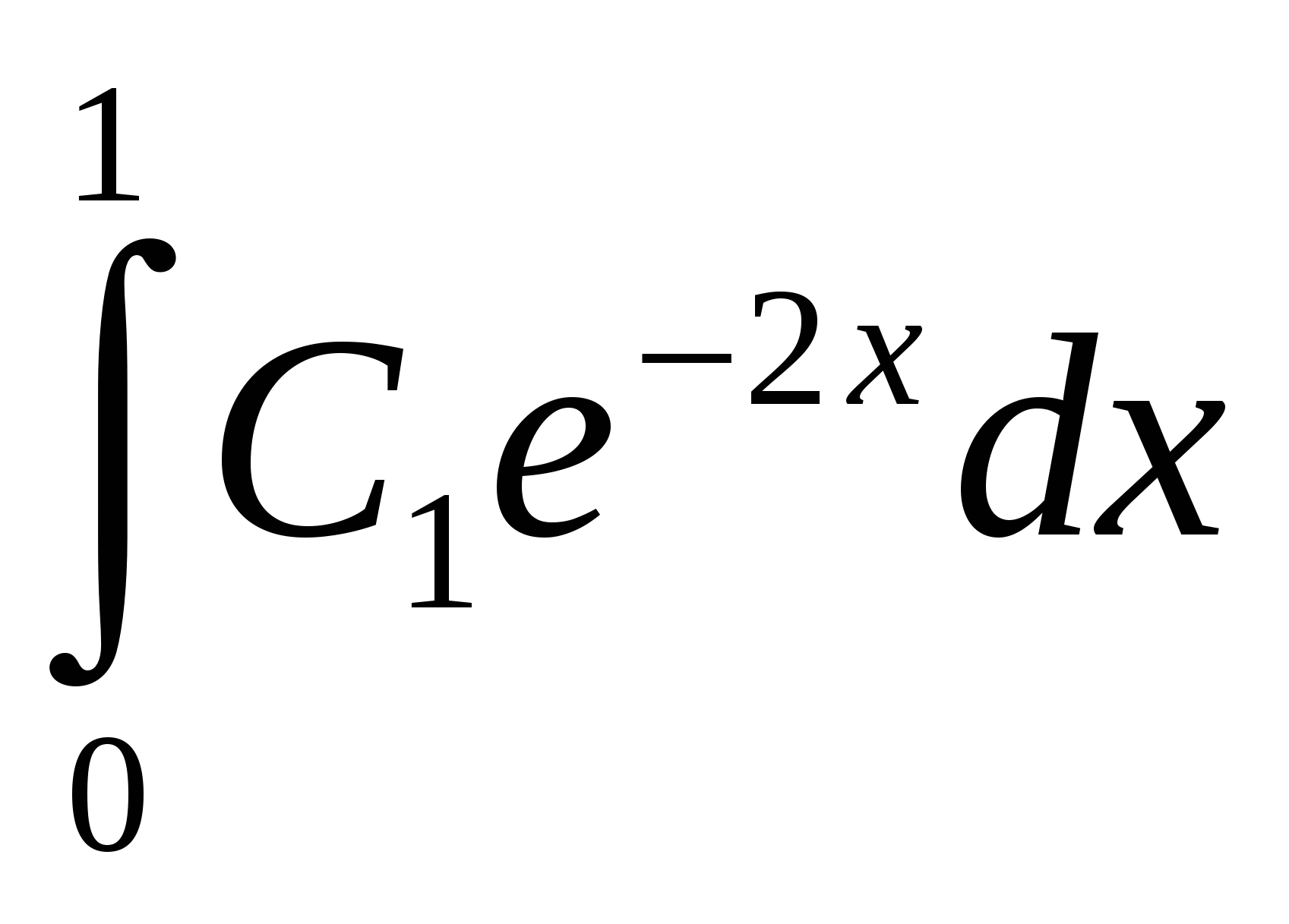

= 1 = = 2 = –С₁ = С₁(1 – e^–2),

откуда

С₁ =  1,1565.

При вычислении интеграла использована четность подынтегральной функции. Функцию распределения F(x) найдем путем интегрирования, причем здесь, в силу свойств функции y = |x| потребуется различать случаи x < 0 и x  0.

При –1  x < 0:

F(x) = = =  = .

При 0  x  1:

F(x) = = + =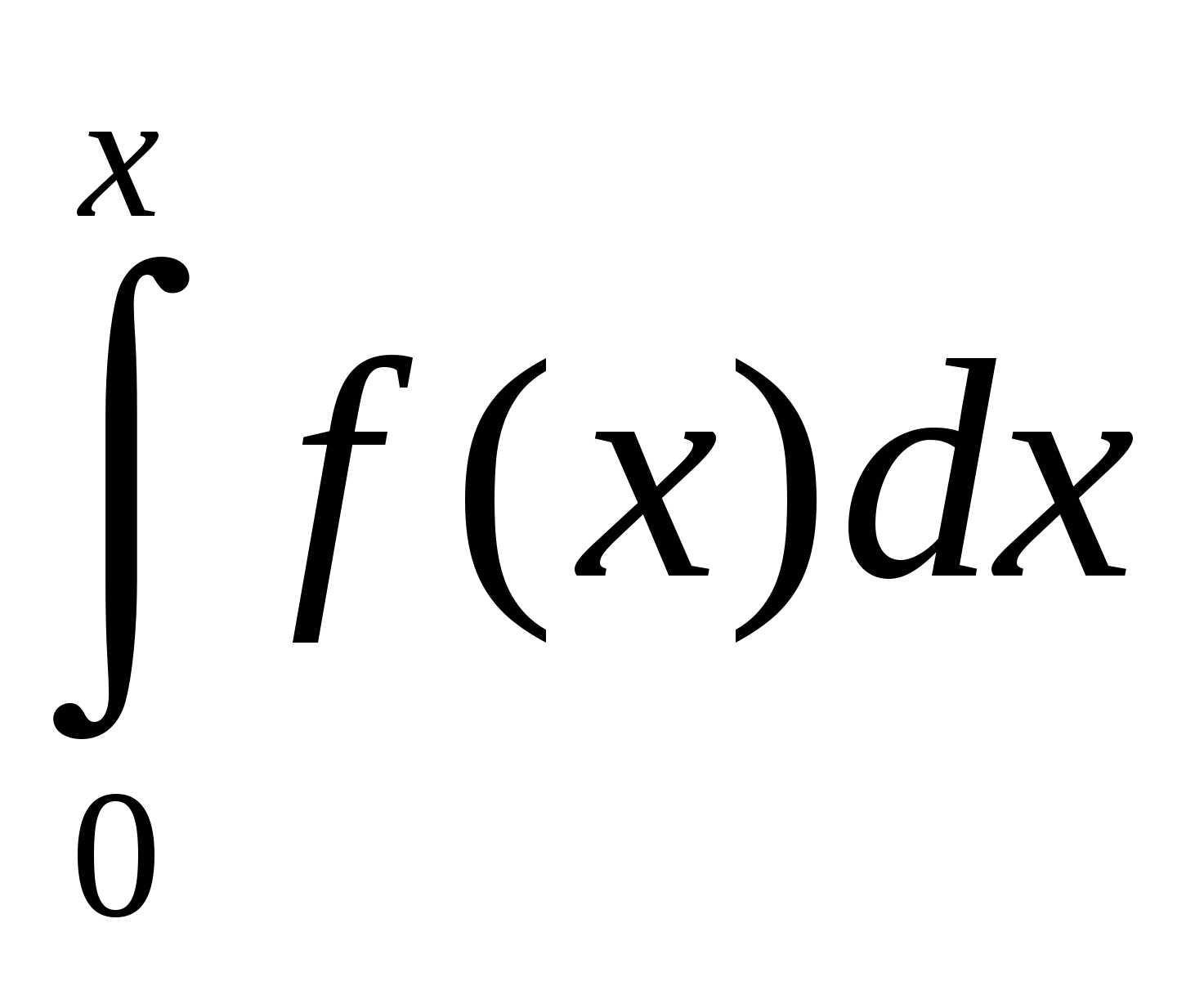

= F(0) + = +  = + ,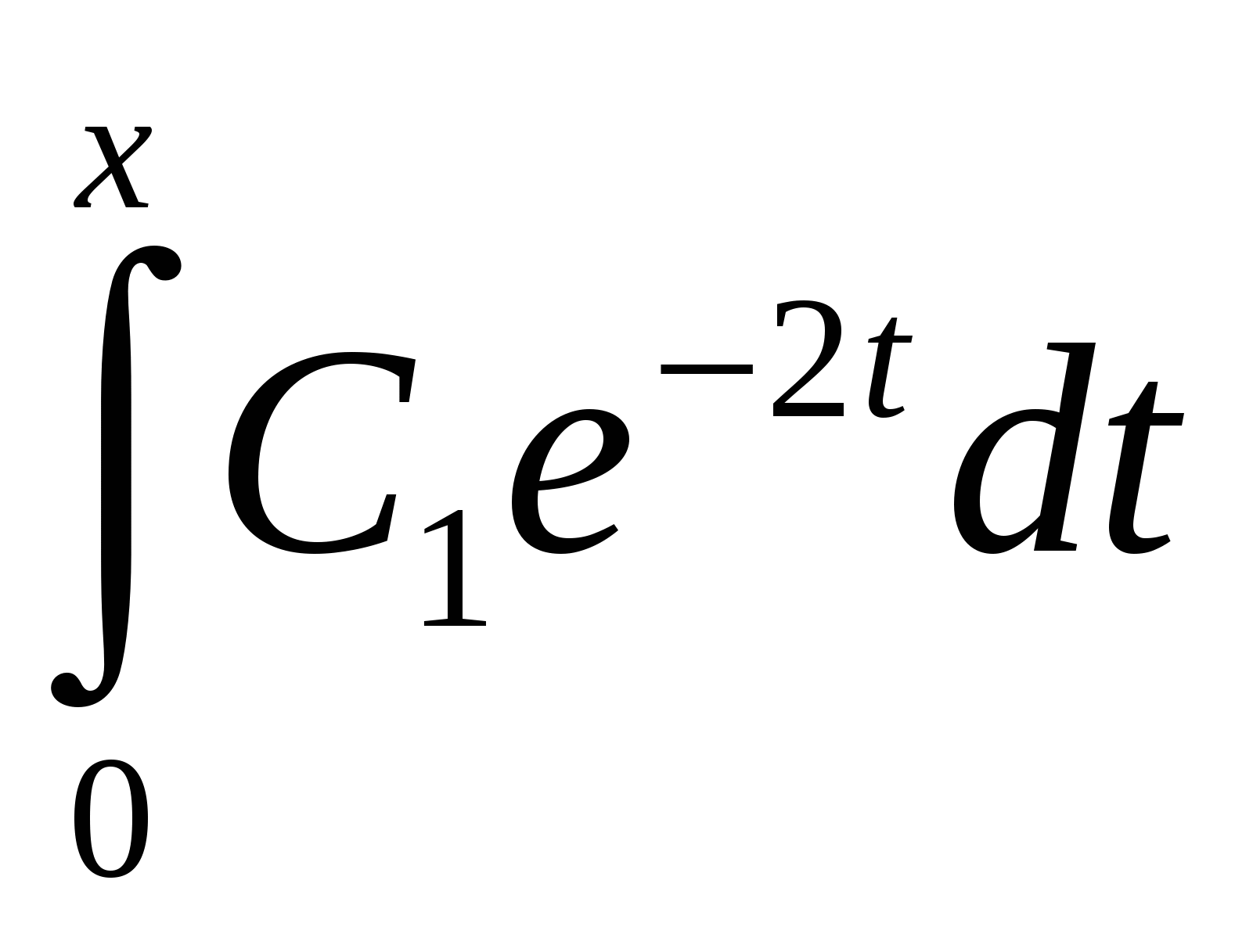
При x < –1 F(x) = 0; при x > 1 F(x) = 1.

Графики плотности функции распределения f(x) и самой функции распределения F(x) представлены на рис. 3 и рис. 4, соответственно.

Рис. 3. График плотности функции распределения вероятностей f(x) н.с.в. X

Рис. 4. График функции распределения вероятностей F(x) н.с.в. X

Рассчитаем числовые характеристики распределения н.с.в. X. Математическое ожидание M(X) н.с.в. X равно:

M(X) = = = 0

в силу нечетности подынтегральной функции. Дисперсия D(X) н.с.в. X равна:

D(X) = 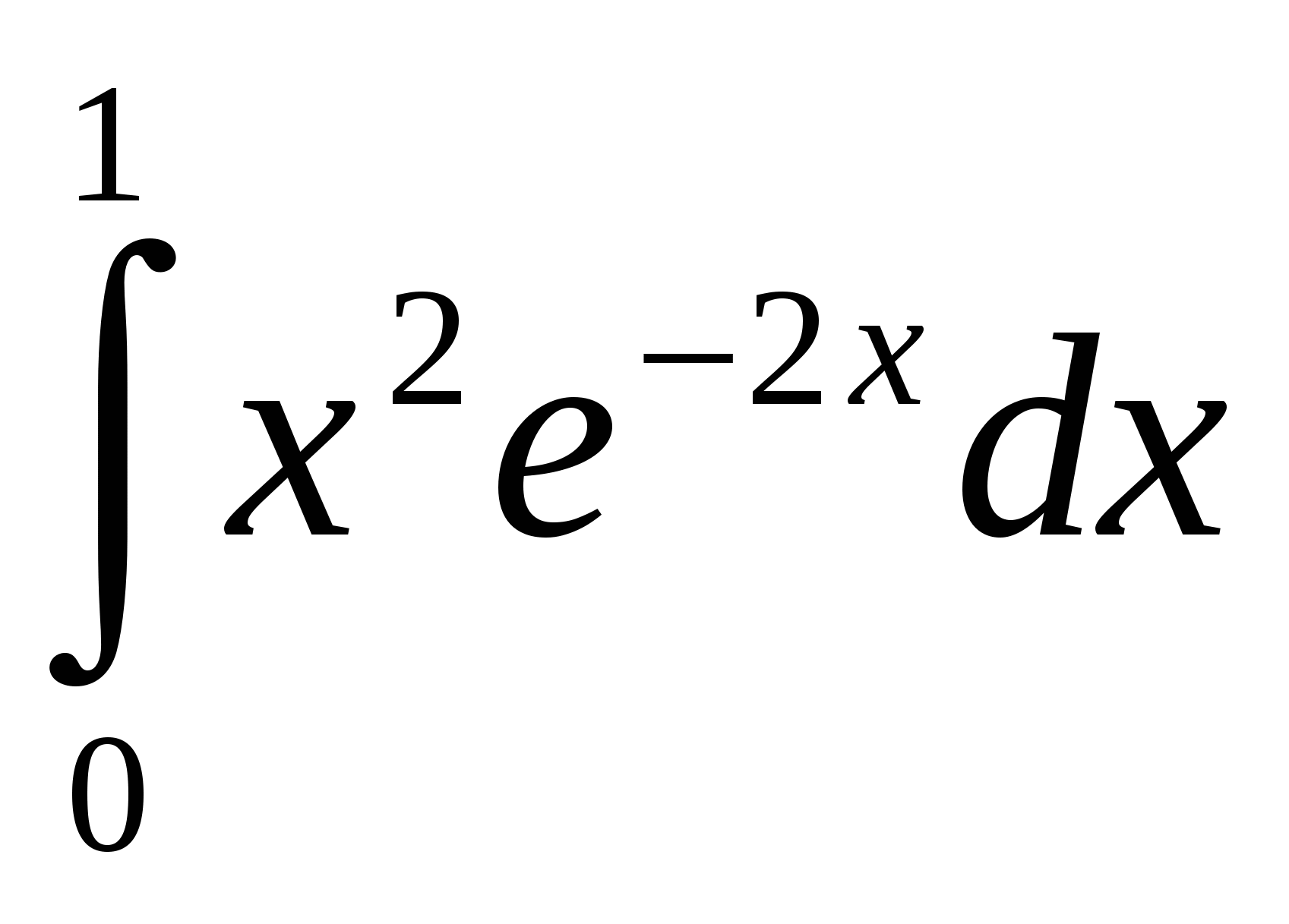= = 2 С₁=  0,1870.

Интеграл в выражении для дисперсии берется двойным интегрированием по частям: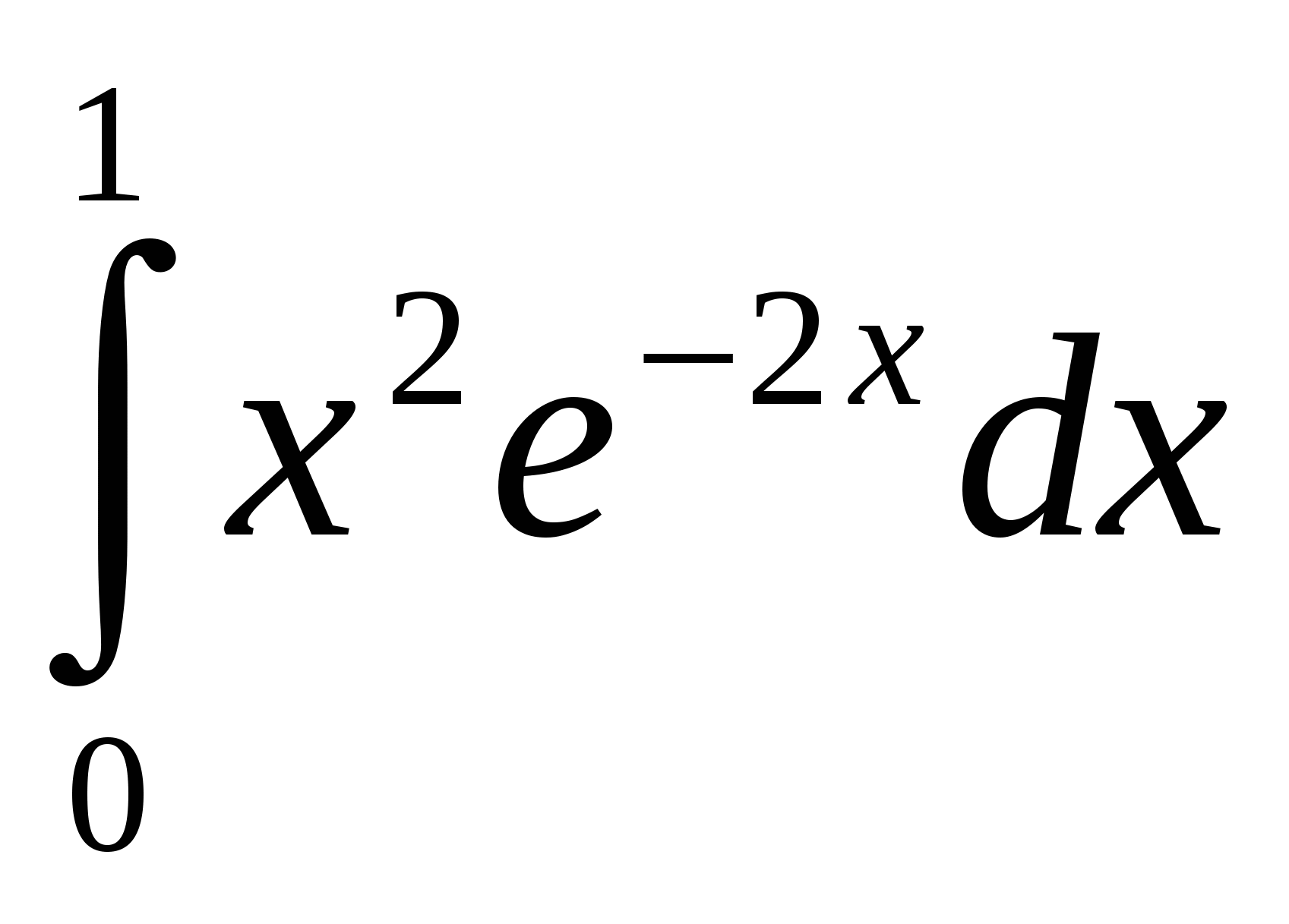

= (1 – 5e^–2)  0,0808.

Среднее квадратическое отклонение СКО найдем как

(X) = = 0,4324.

Наконец, вероятность того, что н.с.в. X примет значения из заданного интервала (a; b) = (1/2; 3/2) вычислим, воспользовавшись найденной функцией распределения:

P(1/2 < x < 3/2) = F(3/2) – F(1/2) = 1 – – =  0,1345.

Ответ: Графики плотности функции распределения f(x) и самой функции распределения F(x) н.с.в. X приведены на рис. 3, 4, соответственно. Вероятность попадания X в интервал (1/2; 3/2) равна P(1/2 < x < 3/2) = 0,1345. Числовые характеристики распределений: математическое ожидание M(X) = 0; дисперсия D(X) = 0,1870; СКО (X) = 0,4324.

ИДЗ-12. Статистическое распределение случайной величины и его числовые характеристики.

Представлены статистические данные. Требуется: 1) составить дискретный вариационный ряд, при необходимости упорядочив его; 2) определить основные числовые характеристики ряда; 3) дать графическое представление ряда в виде полигона (гистограммы) распределения; 4) сформулировать содержательные выводы.

Прим. 1) При проверке статистической гипотезы о виде распределения принять уровень значимости  = 0,05; 2) Для числовой обработки данных рекомендуется использовать подходящий математический пакет, например, электронную таблицу MS Excel.

Результаты измерений диаметров n = 200 валков после шлифовки обобщены в табл. 3 (мм):

Таблица 3

Частотный вариационный ряд диаметров валков.

i	1	2	3	4	5	6	7	8
xi, мм	6,68	6,69	6,7	6,71	6,72	6,73	6,74	6,75
ni	2	3	12	6	11	14	30	25

i	9	10	11	12	13	14	15	16
xi, мм	6,76	6,77	6,78	6,79	6,8	6,81	6,82	6,83
ni	27	31	14	8	5	6	5	1

Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.

Решение: Основные числовые характеристики данного вариационного ряда найдем по определению. Средний диаметр валков равен (мм):

x_ср = = 6,753;

исправленная дисперсия (мм²):

D = = 0,0009166;

исправленное среднее квадратическое (стандартное) отклонение (мм):

s = 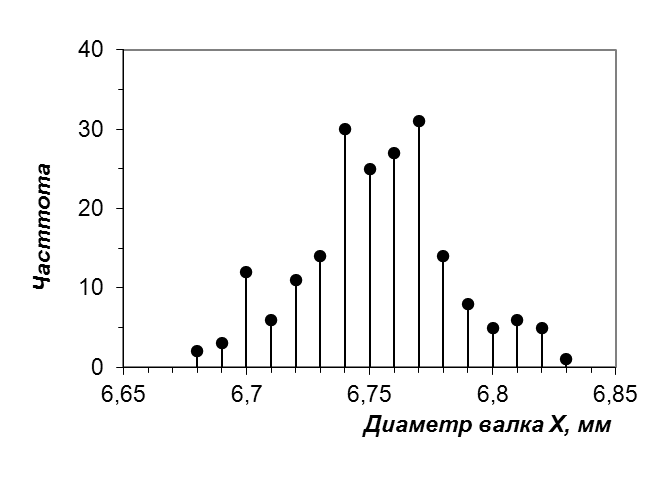= 0,03028.



Рис. 5. Частотное распределение диаметров валков
Исходное («сырое») частотное распределение вариационного ряда, т.е. соответствие n_i(x_i), отличается довольное большим разбросом значений n_i относительно некоторой гипотетической «усредняющей» кривой (рис. 5). В этом случае предпочтительно построить и анализировать интервальный вариационный ряд, объединяя частоты для диаметров, попадающих в соответствующие интервалы.

Число интервальных групп K определим по формуле Стерджесса:

K = 1 + log₂n = 1 + 3,322lgn,

где n = 200 – объем выборки. В нашем случае

K = 1 + 3,322lg200 = 1 + 3,3222,301 = 8,644  8.

Ширина интервала равна (6,83 – 6,68)/8 = 0,01875  0,02 мм.

Интервальный вариационный ряд представлен в табл. 4.
Таблица 4

Частотный интервальный вариационный ряд диаметров валков.

k	1	2	3	4	5	6	7	8
xk, мм	6,68 – 6,70	6,70 – 6,72	6,72 – 6,74	6,74 – 6,76	6,76 – 6,78	6,78 – 6,80	6,80 – 6,82	6,82 – 6,84
nk	5	18	25	55	58	22	11	6

Интервальный ряд может быть наглядно представлен в виде гистограммы частотного распределения (рис. 6).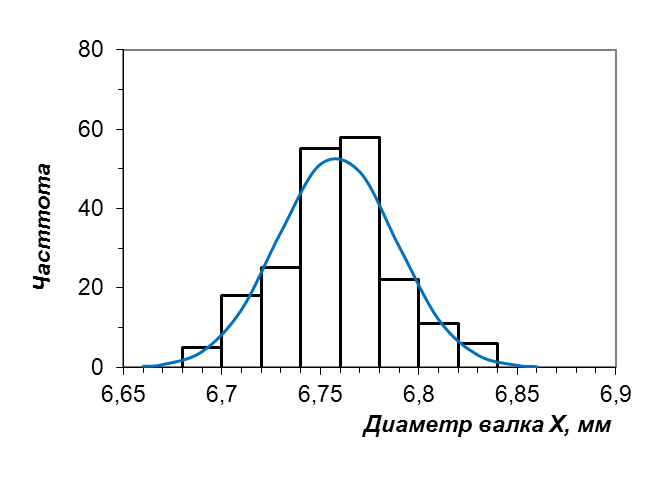



Рис. 6. Частотное распределение диаметров валков. Сплошная линия – сглаживающая нормальная кривая.

Вид гистограммы позволяет сделать предположение о том, что распределение диаметров валков подчиняется нормальному закону, согласно которому теоретические частоты могут быть найдены как

n_{k, теор} = nN(a; ; x_k)x_k,

где, в свою очередь, сглаживающая гауссова кривая нормального распределения определяется выражением:

N(a; ; x_k) = .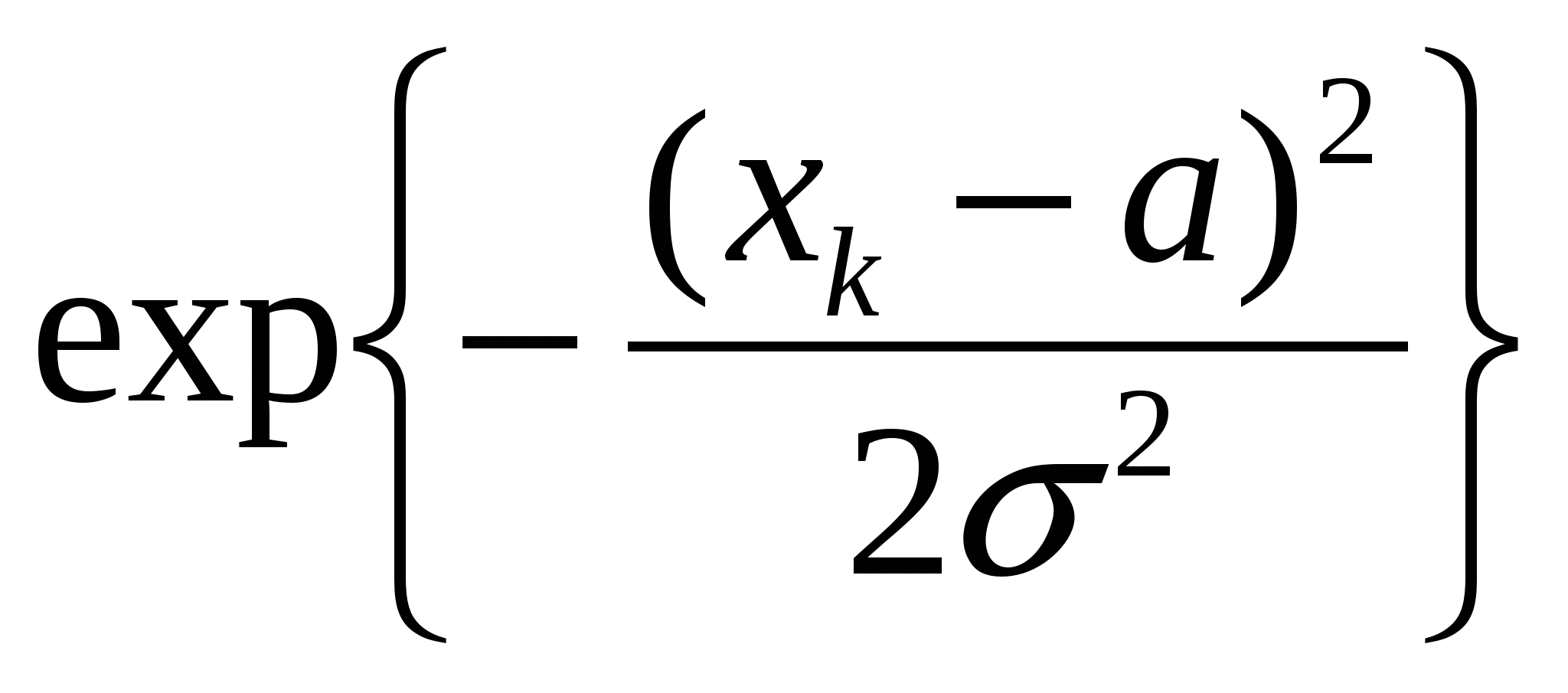

В этих выражениях x_k – центры интервалов в частотном интервальном вариационном ряде табл. 4. Например, x₁ = (6,68 + 6,70)/2 = 6,69. В качестве оценок центра a и параметра  гауссовой кривой можно принять:

a = x_ср;  = s.

Из рис. 6 видно, что гауссова кривая нормального распределения в целом соответствует эмпирическому интервальному распределению. Однако следует удостовериться в статистической значимости этого соответствия. Используем для проверки соответствия эмпирического распределения эмпирическому критерий согласия Пирсона ² [2-4]. Для этого следует вычислить эмпирическое значение критерия как сумму

² = ,

где n_k и n_k,_теор – эмпирические и теоретические (нормальные) частоты, соответственно. Результаты расчетов удобно представить в табличном виде (табл. 5):

Таблица 5

Таблица вычисления критерия Пирсона

[xk, xk+1), мм	xk, мм	nk	nk,теор
6,68 – 6,70	6,69	5	4,00	0,25
6,70 – 6,72	6,71	18	14,57	0,81
6,72 – 6,74	6,73	25	34,09	2,42
6,74 – 6,76	6,75	55	51,15	0,29
6,76 – 6,78	6,77	58	49,26	1,55
6,78 – 6,80	6,79	22	30,44	2,34
6,80 – 6,82	6,81	11	12,07	0,09
6,82 – 6,84	6,83	6	3,07	2,80
			2эмп	10,55

Критическое значение критерия найдем по таблице Пирсона [2, 3] для уровня значимости  = 0,05 и числа степеней свободы d.f. = K – 1 – r, где K = 8 – число интервалов интервального вариационного ряда; r = 2 – число параметров теоретического распределения, оцененных на основании данных выборки (в данном случае, – параметры a и ). Таким образом, d.f. = 5. Критическое значение критерия Пирсона есть ²_крит(; d.f.) = 11,1. Так как ²_эмп < ²_крит, заключаем, что согласие между эмпирическим и теоретическим нормальным распределением является статистическим значимым. Иными словами, теоретическое нормальное распределение удовлетворительно описывает эмпирические данные.