Экономическая статистика. Контрольная работа. Валовая продукция, млн руб
 Скачать 35.86 Kb. Скачать 35.86 Kb.
|
|
Задача 5.1. За отчетный период деятельность группы предприятий характеризуется следующими данными на основании статистического и финансового учета:
По данным таблицы произвести группировку предприятий по размеру основных фондов, выделив 4 группы (60%). Установить зависимость прибыли предприятия от численности работников, стоимости основных фондов и объема выпускаемой продукции (30%). Сделать выводы (10%). Решение Для группировки предприятий по размеру основных фондов находим величину интервала, которая определяется по формуле: i=X max-X min/k, где k = 4 i=1590–176/4=353.5 Валовая продукция
Численность персонала
Прибыль
Для установления зависимости прибыли предприятия от размера, численности и объема выпускаемой продукции необходимо сделать группировку по прибыли. i =X max-X min/k i = 113-27/4=21.5. К первому интервалу принадлежит 5 предприятий, ко второму 5, к третьему 4, к четвертому 2. Как видно из приведенных выше таблиц, предприятия по размеру основных производственных фондов распределены неравномерно. Наибольший % к итогу по валовой продукции 37,4%, по численности персонала – 31,81% и по получению прибыли – 34,75%, принадлежит предприятиям со среднегодовой стоимостью производственных фондов от 883 млн. руб. до 1236,5 млн. руб. Таким образом, можно сказать, что при увеличении производственных фондов, происходит увеличение валовой продукции и прибыли. Соответственно между этими показателями существует прямая связь, чего нельзя сказать о зависимости, прибили и среднесписочной численностью персонала. Задача 5.2.
Обоснуйте правильность выбора формулы для расчета (20%). Решение Х = 377/ (70/11 + 36/5 + 60/14 + 136/8 + 65/13) = 377/39,84 = 9,46 Обоснование: Мы рассчитали среднюю дальность перевозки 1 тонны каждого отдельно взятого автомобиля, после чего если взять общий грузооборот и поделить на среднюю дальность перевозки всех автомобилей мы получили среднюю дальность перевозки 1 тонны груза. Ответ: 9,46 км средняя дальность перевозки 1 т. груза Задача 5.3.В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 2 % изделий получены следующие данные о весе обследованных единиц:
При условии, что к стандартной продукции относятся изделия с весом от 2001 до 2100 г, установите для всей партии: с вероятностью 0,95 возможны пределы удельного веса стандартной продук- ции (50%); с вероятность 0,997 возможные пределы среднего веса одного изделия в ге- неральной совокупности (50%). Решение 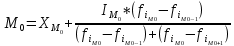 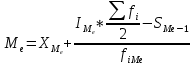 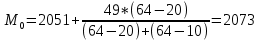 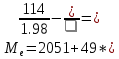 Задача 5.4.Имеются следующие данные о распределении строительных бригад области по производительности труда и себестоимости единицы продукции:
Рассчитайте коэффициент взаимной сопряженности Пирсона (80%). Сде- лайте вывод (20%). Z1= (169/73 + 289/58 + 1024/63) / 62 = 0,378 Z2= (441/73 + 961/58 + 484/63) / 74 = 0,409 Z3= (1521/73 + 100/58 + 81/63) / 58 = 0,411 φ2=0,378+0,409+0,411–1=0,198 Kп= 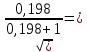 0.406 0.406Вывод: коэффициент взаимной сопряженности Пирсона заметно отличается от нуля - между себестоимостью продукции и производительностью труда существует слабая связь. Ответ: 0.406 коэффициент взаимной сопряженности Пирсона Задача 5.5.Имеются следующие данные о товарных запасах торгового предприятия (тыс. руб., сопоставимые данные):
Определите абсолютное (40%) и относительное (40%) изменение средней суммы товарных запасов в 2017 г. по сравнению с 2014, 2015 и 2016 гг. Интерпретируйте полученные результаты (20%). Решение Средняя сумма товарных запасов: 2014 = 294 / 4 = 73,5 2015 = 314 / 4 = 78,5 2016 = 330 / 4 = 82,5 ∆ Q = 82,5 -73,5= 9 тыс. руб. Средняя сумма в 2016 году по сравнению с 2014 выросла на 9 тыс. руб. 2014 = 100% 2016 = (82,5/73,5) *100 = 112% ∆ = (96–72) / (13–1) =2 Средняя сумма с 2014 по 2016 год возросла на 12% Прогноз на 2017 год: 3+7+7+7Задача 5.6.Имеются данные о себестоимости и объеме продукции предприятия. Опре- делите: агрегатный индекс себестоимости продукции (по модели Пааше) (30%); агрегатный индекс физического объема продукции (по модели Ласпейреса) (30%); общий индекс затрат на производство (30%).
Покажите взаимосвязь между индексами (10%). Решение Вычислим индивидуальные индексы себестоимости А = 146/136 = 1,073 или 107,3% + 7.3% Б = 80/90 = 0,888 или 88,8% - 11,2% А = 118/110 = 1,072 или 107,2% + 7,2% Вычислим индивидуальные индексы физического объема продукции А = 1000/1100 = 0,909 или 90,9% -9,1% Б = 4500/3900 = 1,153 или 115,3% + 15,3% В = 4600/5100 = 0,901 или 90,1% - 9,9% Агрегатный индекс себестоимости по Пааше 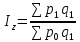 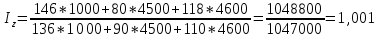 Агрегатный индекс физического объема по Ласпейреса 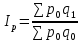  Общий индекс затрат на производство продукции 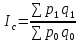 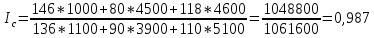 Взаимосвязь 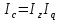 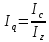 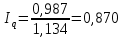 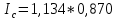 = 0,986 = 0,9861,012 * 0,870 = 0,880 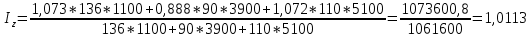 Агрегатный индекс Агрегатный индекс | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
