Вариант 1 Установите соответствие Определение Свойства 1)убывающая А) f(x)f(x) 2)чётная Б) f(x) f(x) 3)возрастающая В) f(xТ)f(x) 4)нечётная Г) f(x1)
 Скачать 464.4 Kb. Скачать 464.4 Kb.
|
|
а)у/= 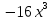 б) у/= б) у/=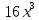 в) у/= в) у/=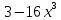 г) у/= г) у/=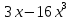 д) у/= д) у/=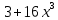 10. Вычислите производную функции 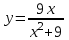 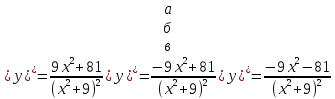 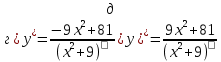 11. Найти производную функции у = (5х2 + 10) а) у/ = 5х2 б) у/ = 10х в) у/= 10х+1 г) у/ = 5х+1 д) у/ = 5х 12.Найти точки экстремума функции  а) нет экстремума б)х=0,5 – т. макс., х= 2 – т. мин в) х=2 – т. мин. г) х=0,5 – т. макс. д) х=0 – т. макс. а) нет экстремума б)х=0,5 – т. макс., х= 2 – т. мин в) х=2 – т. мин. г) х=0,5 – т. макс. д) х=0 – т. макс.13.Найти интеграл: 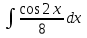 а) 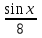 + С; б)sin2x +C; в) + С; б)sin2x +C; в)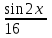 + C ; г)-sin + C ; г)-sin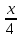 + C; д)- + C; д)-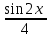 + C. + C.1 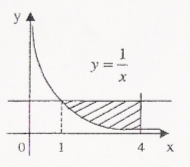 4. Выразите с помощью определенного интеграла площадь заштрихованной фигуры: 4. Выразите с помощью определенного интеграла площадь заштрихованной фигуры:а) 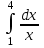 ; б) ; б) 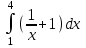 ; в) ; в) 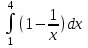 ; ; г) 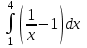 ; д) ; д) 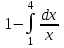 . .15.Площадь основания тетраэдра равна 32 см2. Найти площадь полной поверхности. а) 160 б) 32/3 в)8 г) 128 д) 96 16. Какая фигура получается при сечении цилиндра плоскостью, параллельной оси цилиндра а) трапецией б)треугольником в)прямоугольником г) ромбом д) кругом 17.Объём пирамиды равен: а)V= abc б)V=Sоснh в)V=  Sоснh г)V= Sоснh г)V= Sоснh д)V=1/6 Sоснh Sоснh д)V=1/6 Sоснh18. Даны векторы  = (-1,2), = (-1,2),  = (0,3). Найдите координаты вектора 2 = (0,3). Найдите координаты вектора 2 + + а) (-1,5) б) (2,7) в) (-2,7) г) (-2,5) д) (0,5) 19. Найдите скалярное произведение векторов  =(0,3), =(0,3),  =(3,4) =(3,4) а) (-3,-8) б) -8 в)-12 г) 12 д) 0 20.Решите уравнение: 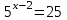 а) х= -1;х=4 б) х=1; в) х=0 ; г)х=4; д)х=1/4. а) х= -1;х=4 б) х=1; в) х=0 ; г)х=4; д)х=1/4.21.Логарифмическая функция монотонно убывает при: а)а>1, б)а<1 , в)0<а<1, г)а≤0, д)а  0. 0. 22.Определите неверное равенство: 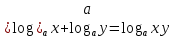 б) б) =1 =1 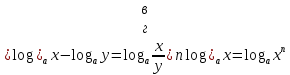 д) д)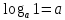 23.Вычислите: 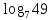 а) -2 ; б) 1/2; в) –7 ; г)2; д)7. а) -2 ; б) 1/2; в) –7 ; г)2; д)7.24.Решите уравнение: 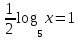 а) -25; б) а) -25; б)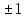 ; в) 5 ; г)25; д)-5. ; в) 5 ; г)25; д)-5.25.Решите неравенство: 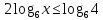 а) (-¥;0)È(2;+ ¥) б)(0;2) в) (-¥;0]È[2;+ ¥) г) (0;2] д) (-2;2). Вариант №4 1. Какая из функций является чётной: 1) y=x+cosx 2)y=cosx-x3 3) y=2х2 +4cosх; 4) y=2x7 +3x3 5) y=x2+sinx а) 4 б) 5 в) 1,2 г) 3,5. д) 3. 2. Установите точки разрыва функции 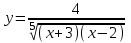 а) -3;2 б) -3;4 в) 2 г) 0 д) всюду непрерывна. 3.Определите промежутки возрастания функции, изображенного на рисунке: 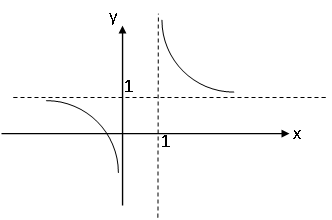 а)(-¥;+¥) б)(-¥;0)È(1;+ ¥) в) нигде г) (-¥;0)È(0;+ ¥) д) (-¥;0). а)(-¥;+¥) б)(-¥;0)È(1;+ ¥) в) нигде г) (-¥;0)È(0;+ ¥) д) (-¥;0).4.Функция называется периодической, если для любого аргумента х выполняется равенство: а) f(-x)=f(x) б) f(-x)= - f(x) в)f(x+Т)=f(x) г) f(x1) 5.Вычислите: arcctg (  ), а) ), а) б) 1; в) б) 1; в) г) г) ; д) ; д)  . .6.Решите уравнение: sinx= 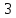 а) 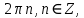 б) нет решения в) б) нет решения в) г г ; д) ; д)  n n Z Z7. Определите значение функции: arctg 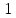 - arcctg - arcctg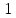 - arccos - arccos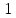 а) 1 б) 0 в)  г) г)  д) -1 д) -18.Если в точке х функции U и V имеют производные U/ и V/,то в этой точке существует производная частного ( 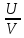 )/: а) у/ = U/+V/ б) у/ =1 в) у/ = U/∙V+ V/∙U г) у/ =0 д) у/= )/: а) у/ = U/+V/ б) у/ =1 в) у/ = U/∙V+ V/∙U г) у/ =0 д) у/= 9. Вычислите производную функции 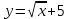 х х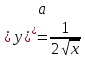 б) б)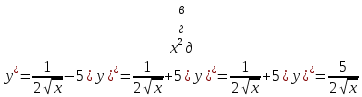 10. Найти точки максимума функции: 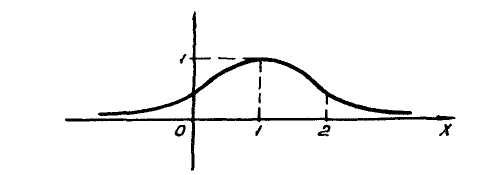 а)x=1,x=0 б)x=2 в)x=0,x=1,x=2 г)x=1 д)x=1,x=2, а)x=1,x=0 б)x=2 в)x=0,x=1,x=2 г)x=1 д)x=1,x=2,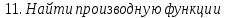  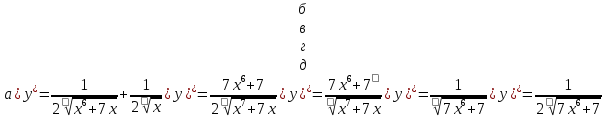 12. Установите соответствие Функция Производные 1) у = 2cos3x А) у/ = -3sin3х 2)у = cos3x Б) у/ = -3sin3х/2 3) у= cos3x/2 В) у/ = 6/cos23x 4) у = 2tg3х Г) у/ = -6sin3x. а) 1А,2Г,3Б,4В б) 1Г,2А,3Б,4В в) 1В,2А,3Б,4Г г) 1В,2Г,3Б,4А д) 1Б,2Г,3В,4А. 13. Найти интеграл: 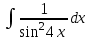 а) –сtg 4x + c; б) tg4x + c ; в) 4 сtg 4x + c; г) 4 сtg 4x + c; д) -  сtg 4x + c. сtg 4x + c.14. Какая из следующих функций является первообразной для функции: 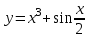 а) 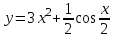 ; б) ; б) ; в) ; в) 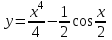 ; г) ; г)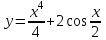 ; д) ; д)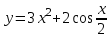 . .15. Вычислить интеграл 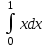 : а)1; б)1/2; в) 1/3 ; г) 1/4; д) 1/5. : а)1; б)1/2; в) 1/3 ; г) 1/4; д) 1/5.16.Основание призмы - квадрат со стороной 4 см. Боковое ребро призмы равно 5 см. Найдите Sбок. а) 16 б) 20 в)8 г) 80 д) 40 17. Как должны быть расположены две равные окружности, чтобы через них можно было провести цилиндрическую поверхность? а)параллельно б)перпендикулярно в) пересекаться г)совпадать д) не имеет значения 18.Объём прямого кругового цилиндра равен: а)V=abc б)V=Sоснh в)V=  Sоснh г)V= Sоснh г)V= Sоснh д)V= 1/6Sоснh Sоснh д)V= 1/6Sоснh19. Скалярное произведение векторов 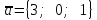 , , 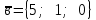 равно равноа) 15 б) 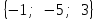 в) 17 г) в) 17 г) 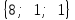 д) 8. д) 8.20.Найти модуль вектора `а=(-1;2) а) 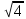 б) б)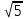 в)1 г) в)1 г) д)0 д)021.Даны координаты точек А (1; 1),Д( 5; 3). Найдите координаты середины отрезка АД а) (6;4) б)40 в)(2;1) г)20 д) (3;2) 22. Найти интеграл: 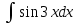 а)-соs3х + С; б) 3 соs 3х + С; в) 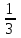 cоsх + С ; г)- cоsх + С ; г)- 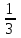 соs3х + С; д) соs3х + С; д) 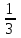 х + С. х + С.23.Решите уравнение: 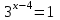 а) х= -1;х=4 б) х=1; в) х=0 ; г)х=4; д)х=1/4. а) х= -1;х=4 б) х=1; в) х=0 ; г)х=4; д)х=1/4.24.Найдите область определения функции:  а) (-¥;0,5)È(1;+ ¥) б)(0,5;1) в) (-¥;0,5]È[1;+ ¥) г) [0,5;1] д) [-0,5;1). 25. Исследовать на непрерывность функцию  , указать точки разрыва , указать точки разрываа) 5 б) -5 в) -1,1 г) -1,1,5 д) 1,5 Вариант №5 1. Какая из функций является чётной: 1) y=x+cosx 2)y=cosx 3) y=5x4 +2x2 4) y=2x7 +3x3 5) y=x2+sinx а) 4 б) 5,3 в) 1,2 г) 3 д)2,3. 2 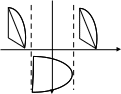 .Определите промежутки возрастания функции, изображенного на рисунке: .Определите промежутки возрастания функции, изображенного на рисунке:а)(-¥;+¥) б)(-¥;-2)È(2;+¥) в) (2;+¥) г) (-¥;-2)È(-2;0) д) (-¥;-2). 3.Функция называется нечётной, если для любого аргумента х выполняется равенство: а)f(-x)=f(x) б) f(-x)= - f(x) в) f(x+Т)=f(x) г) f(x1) 4.Определите значение функции sin 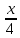 а) а)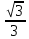 б) 1; в) б) 1; в) ; г) ; г)  ; д) ; д) 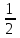 . .5.Решите уравнениe: tgx=0 а)-  +πk, k +πk, k Z б) πn, n Z б) πn, n Z, в) Z, в)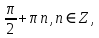 г) г)  ; д) ; д)  n n Z Z6. Решите неравенство: sinx<0 a  πk πk 2πk, k 2πk, k Z б) Z б) x x в)  г) г) 2πk, k 2πk, k Z д) Z д) 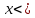 πk, k πk, k Z Z7. Определите значение функции: arctg  +arcsin +arcsin +arccos +arccos а)  б) 0 в) π г) 1 д) -1 б) 0 в) π г) 1 д) -18.Производной функцииу(х) в точке х, называется предел: а) 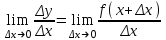 б) б)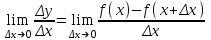 в) 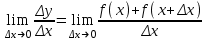 г) г) 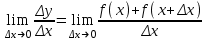 д) 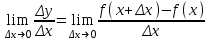 9. Точкой максимума функции, называется точка, если функция y(х) в точке х0 непрерывна, а на интервале (а,х0): а)у/>0 б) у/< 0 в)у/= 0 г) у//< 0 д)у//> 0 10. Вычислите производную функции 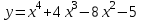 а)у/= 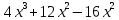 ; б)у/= ; б)у/= ; ;в)у/=  ; г)у/= ; г)у/= д)у/= д)у/= ; ;11.Вычислить 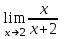 а) 1 б) 1/2 в)2/3 г) 0 д) 1/4. а) 1 б) 1/2 в)2/3 г) 0 д) 1/4.12. Исследовать на непрерывность функцию 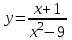 , указать точки разрыва , указать точки разрываа) 3,-3 б) -1 в) 1 г) 1,3,-3 д)-1,3,-3 13. Какая из следующих функций является первообразной для функции: 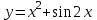 а) 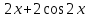 б) б) 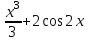 в) в)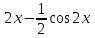 г) г) 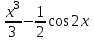 д) д) 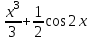 . .14. Укажите формулу Ньютона-Лейбница 1) 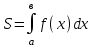 2) 2) 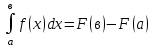 3) 3)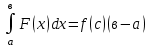 4) 4) 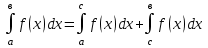 а) 1; б) 2; в)3; г)4; д) нет правильного ответа. 15. Вычислить интеграл 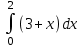 : а) 10 ; б) 2; в) –10 ; г) –8; д) 8. : а) 10 ; б) 2; в) –10 ; г) –8; д) 8.16.Фигура, полученная при вращении прямоугольного треугольника вокруг одного из катетов, называется: а) шаром б)конусом в)цилиндром г)пирамидой д) призмой 17.Сколько диагональных сечений можно провести через одно боковое ребро в четырехугольной призме? а) 1 б) 2 в)5 г)3 д) 4 18.Фигура, полученная вращением полукруга вокруг своего диаметра, называется: |
