Вариант 1 Установите соответствие Определение Свойства 1)убывающая А) f(x)f(x) 2)чётная Б) f(x) f(x) 3)возрастающая В) f(xТ)f(x) 4)нечётная Г) f(x1)
 Скачать 464.4 Kb. Скачать 464.4 Kb.
|
|
а) шаром б)конусом в)цилиндром г)пирамидой д)сферой 19. Найти длину вектора `а-`в, если `а=(1;-2) `в=(-1;0) а) (-2;-2) б)3 в)1 г) (2;-2) д) 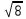 20. Длина ( модуль ) вектора  = ( = (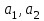 ) это: ) это:а) 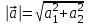 б) б) 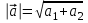 в) в) 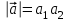 г) г) 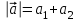 д) д) 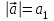 21.Решите неравенство: 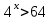 а)(-¥;+¥) б)(-¥;-3)È(3;+¥) в) (3;+¥) г) (-¥;3) д) (-¥;-6). а)(-¥;+¥) б)(-¥;-3)È(3;+¥) в) (3;+¥) г) (-¥;3) д) (-¥;-6).22.Решите неравенство: 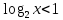 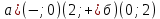 в) (-¥;0]È[2;+ ¥) г) [0;2] д) (-2;2). в) (-¥;0]È[2;+ ¥) г) [0;2] д) (-2;2). 23. 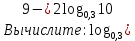 а) -2 ; б) 1/2; в) –1; г)2; д)0,3. а) -2 ; б) 1/2; в) –1; г)2; д)0,3.24.Установить соответствие: 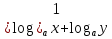 А) А) 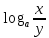 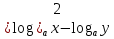 Б) Б) 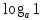 3) 0 В) 1 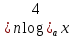 Г) Г) 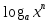 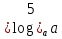 Д) Д) 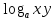 а) 1А, 2Д, 3В, 4Г,5Д б) 1В, 2Б, 3А, 4Д, 5Г в) 1Б, 2Г, 3А, 4В, 5Д г) 1Д, 2А, 3Б, 4Г, 5В д) 1Г, 2А, 3В, 4Б, 5Д 25. 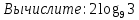 а) -2 ; б) 1/2; в) –1 ; г)2; д)1. а) -2 ; б) 1/2; в) –1 ; г)2; д)1.Вариант №6 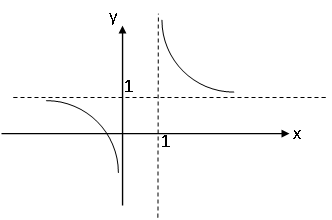 а)(1;+¥) б) (-¥;0)È(1;+ ¥) в) (0;+¥) г) (-¥;0)È(0;+ ¥) д) (-¥;1). а)(1;+¥) б) (-¥;0)È(1;+ ¥) в) (0;+¥) г) (-¥;0)È(0;+ ¥) д) (-¥;1).2.Функция называется чётной, если для любого аргумента х выполняется равенство: а) f(-x)=f(x) б)f(-x)= - f(x) в) f(x+Т)=f(x) г) f(x1) 3. Функция 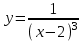 имеет разрыв в точках: имеет разрыв в точках: а) х=1 б) х=1; х=-1 в) х=0 г) точек разрыва нет д) х=2. 4.Определите значение функции sin  а) а)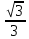 б) 1; в) б) 1; в) ; г) ; г)  ; д) ; д) 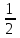 . .5.Решите уравнение: cosx=  а)  arccos ( arccos ( ) +πk, k ) +πk, k Z б) x=πn, n Z б) x=πn, n Z, в) Z, в)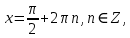 г) 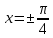 +2πk, k +2πk, k Z д) Z д) 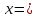 arccos ( arccos (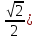 +πk, k +πk, k Z Z6. Упростите выражение: 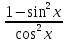 а) а)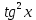 б)1-2 б)1-2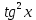 в)1 г) в)1 г) 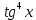 д) -1 д) -17. Вычислите производную функции 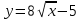 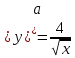 б) б)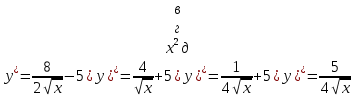 8.Определите промежутки возрастания функции, изображенного на рисунке: 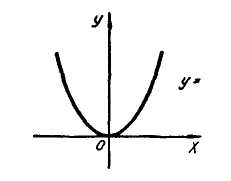 а) (-¥;+¥) б) нет промежутков в) (0;+¥) г) (-¥;0)È(0;+ ¥) д) (-¥;0) 9.Найти интеграл: ∫(2x3-5x2)dx а) x2-5x+c ; б) 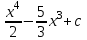 ; в) ; в) 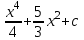 ; г) 2x4-5x3+c; д) ; г) 2x4-5x3+c; д) 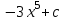 . .10. Укажите формулу, выражающую геометрический смысл определенного интеграла 1) 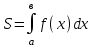 2) 2)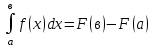 3) 3)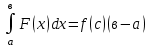 4) 4) 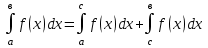 а) 1; б) 2; в) 3; г) 4; д) нет правильного ответа. 11. Вычислите интеграл 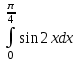 : а) -1/2; б) -1; в) 0; г) 1; д) 1/2. : а) -1/2; б) -1; в) 0; г) 1; д) 1/2.12.Многогранник, одна грань которого произвольный многоугольник, а другие грани – треугольники с общей вершиной, называется: а) шаром б)конусом в)цилиндром г)пирамидой д) призмой 13.Какое число вершин у четырехугольной призмы? а) 6 б) 5 в)8 г)3 д) 4 14.Фигура, полученная вращением полуокружности вокруг своего диаметра, называется: а ) шаром б)конусом в)цилиндром г)пирамидой д)сферой 15. Найти скалярное произведение векторов 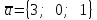 , , 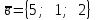 . .а) 15 б) 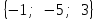 в) 17 г) в) 17 г) 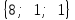 д) 10. д) 10.16. Расстояние между точками А(-5;0) и В(12;0) равно а) 0 б)7 в)-7 г)17 д)  17.Решите уравнение: 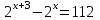 а) х=4 б)х=1; в) х= 6 ; г)х=-6; д)х=-4. а) х=4 б)х=1; в) х= 6 ; г)х=-6; д)х=-4.18. Логарифмическая функция монотонно возрастает при: а)а>1,а≠1 б)а<1 ,а≠1 в)0<а<1,а≠1 г)а≤0,а≠1 д)а  0,а≠1 0,а≠1 19.Определите неверное равенство: 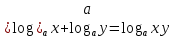 б) б) =0 =0 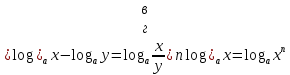 д) д)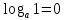 20.Найдите область определения функции:  а) (-¥;0,5)È(1;+ ¥) б)(0,5;1) в) (-¥;0,5]È[1;+ ¥) г) [0,5;1] д) [-0,5;1). 21.Решите уравнение: 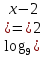 а) -2 ; б) 9; в) 83; г)2; д)79. а) -2 ; б) 9; в) 83; г)2; д)79.22. 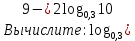 а) -2 ; б) 1/2; в) –1; г)2; д)0,3. а) -2 ; б) 1/2; в) –1; г)2; д)0,3.23. Установите соответствие на интервале (а, в) 1)достаточное условие возрастания функции А) у/< 0 2)достаточное условие убывания функции Б) у/=0 3) условие существования критических точек функции В) у/> 0 а) 1А,2Г,3В б) 1Г,2А,3В в) 1В,2А,3Б г) 1В,2Б,3А д) 1Б,2В,3А. 24.Выразите с помощью определенного интеграла площадь заштрихованной фигуры: а 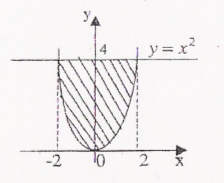 ) )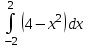 ; б) ; б) 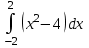 ; в) ; в) 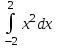 г) г) 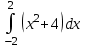 ; ; д) 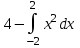 25.Вычислите: 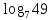 а) -2 ; б) 1/2; в) –7 ; г)2; д)7. а) -2 ; б) 1/2; в) –7 ; г)2; д)7.Вариант №7 1. Определите точки разрыва функции 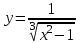 а) ±1 б) 1 в) нет точек разрыва г) 0;-1 д) 0;+1. 2.Определите промежутки возрастания функции, изображенного на рисунке:  y y   2 2   -3 0 3 х -3 0 3 ха) (-¥;+¥) б) (-3;3) в) (-3;+¥) г) (-¥;-3)È(3;+ ¥) д) (-¥;3). 3.Функция называется убывающей, если для любых чисел x1 а) f(-x)=f(x) б) f(-x)= - f(x) в) f(x+Т)=f(x) г) f(x1) 4.Определите значение функции сtg 45о а) 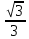 б) 1; в) б) 1; в) ; г) ; г)  ; д) ; д) 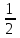 . .5.Решите уравнение: sinx=  а)  +πn, n +πn, n Z, б) Z, б) 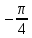 +πn, n +πn, n Z , в) Z , в)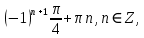 г) г)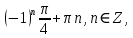 д) д) 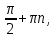 n n Z Z6. Упростите выражение: 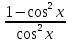 а) 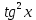 б) б)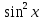 в)1 г) в)1 г) 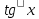 д) -1 д) -1 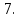 Функция называется возрастающей, если для дифференцируемой функция f(x) в каждой точке промежутка Х производная функции: Функция называется возрастающей, если для дифференцируемой функция f(x) в каждой точке промежутка Х производная функции:а) у/> 0 б) у/< 0 в) у/= 0 г) у//< 0 д)у//> 0 8. Вычислите производную функции y= 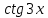 a)у/= 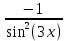 б)у/= б)у/=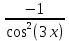 в) у/= в) у/=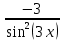 г) у/= г) у/=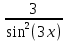 д)у/= д)у/=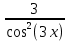 9. Найти производную функции 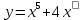 а) у/ = 5х4 б) у/ = 5х4+ 4x в) у/ = х4+ 4 г) у/ = х4 +4x д) у/ = 5х4+ 4 10.Найти предел функции y=f(x): 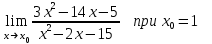 а) 1 б) 16/15 в)-1 г) 0 д)-15/14. 11. Установить соответствие Функция Точки разрыва 1) у = 1/(х2-1) А) х=1 2) у = ех Б) х=+1; х=-1 3)у = 1/(x-1)2 В) точек разрыва нет. а) 1А,2Б,3В б)1А,2В,3Б, в) 1В,2А,3Б г) 1В,2А,3Б д) 1Б,2В,3А. 12.Найдите ошибку: а) 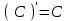 б) б)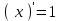 в) в)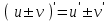 г) г)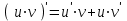 д) д)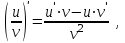 13. Найти интеграл: 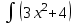 dx dxа) 3x 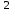 + 4 + c ; б)x + 4 + c ; б)x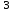 + 4x + c; в) 6x + c; г) x + 4x + c; в) 6x + c; г) x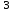 + c; д) ln + c; д) ln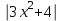 + c; + c;14. Вычислите интеграл 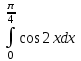 : : а) 0; б) 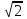 ; в) 1/2; г) -1/2; д) 1. ; в) 1/2; г) -1/2; д) 1.15.Площадь полной поверхности тетраэдра равна 400 см2. Найти площадь основания тетраэдра. а) 100 б) 400/3 в)400/5 г)1600 д) 1200 16.Тело, ограниченное конической поверхностью и кругом, называется: а) шаром б)конусом в)цилиндром г)пирамидой д) призмой 17.Объём призмы равен: а)V=abc б)V=Sоснh в)V=  Sоснh г)V= Sоснh г)V= Sоснh д)V= 1/6Sоснh Sоснh д)V= 1/6Sоснh18. Длина ( модуль ) вектора  = ( = (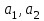 ) это: ) это:а) 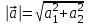 б) б) 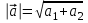 в) в) 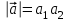 г) г) 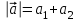 д) д) 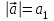 19. Найти скалярное произведение векторов`а и `а+в если `а=(1;2) `в=(0;1) а) 3 б)(1;2) в) (-1;-6) г)7 д)1 20.Решите уравнение: 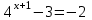 а) х= -1;х=4 б)х=1; в) х=-1 ; г)х=4; д)х=1/4. а) х= -1;х=4 б)х=1; в) х=-1 ; г)х=4; д)х=1/4.21.Решите неравенство: 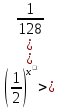 а)(6;+¥) б) (-¥;-7)È(7;+¥) в) (7;+¥) г) (-¥;6) д) (-¥;7). 22.Найдите область определения функции:  а) (-¥;0,5)È(1;+ ¥) б)(0,5;1) в) (-¥;0,5]È[1;+ ¥) г) [0,5;1] д) [-0,5;1). 23.Определите неверное равенство: 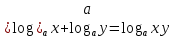 б) б) =1 =1 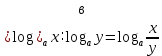 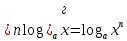 д) д)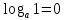 24. . 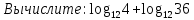 а) -2 ; б) 1/2; в) 1 ; г)2; д)12. 25. .Решите уравнение: 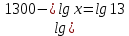 а) -1; б) 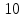 ; в)1 ; г)100; д)-10. ; в)1 ; г)100; д)-10.Вариант №8 1. Функция 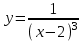 имеет разрыв в точках: имеет разрыв в точках:а) х=1 б) х=1; х=-1 в) х=0 г) точек разрыва нет д) х=2. 2.Определите промежутки возрастания функции, изображенного на рисунке: 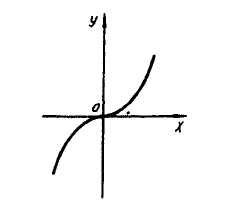 а)(-¥;+¥) б)нигде в) (0;+¥) г) (-¥;0)È(0;+ ¥) д) (-¥;0). а)(-¥;+¥) б)нигде в) (0;+¥) г) (-¥;0)È(0;+ ¥) д) (-¥;0).3. Найти область определения функции у = 1/  |
