|
|
Эконометрика. КР_Эконометрика. Вариант 8 Построение спецификации эконометрической модели
Вариант 8
1. Построение спецификации эконометрической модели
Динамика реальной заработной платы оказывает влияние на динамику объема ВВП. Связь между признаками прямая. Т.е. с увеличением реальной заработной платы объем ВВП тоже увеличивается.
Соответственно и индексы показателей также имеют корреляционную связь.
Независимой переменной Х является «Индекс реальной зарплаты». Зависимой переменной Y выступает «Индекс реального ВВП».
Парная линейная регрессия определяется моделью вида: 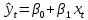
2. Исследование взаимосвязи показателей с помощью диаграммы рассеяния и коэффициента корреляции
Строим диаграмму рассеяния (рисунок 1)
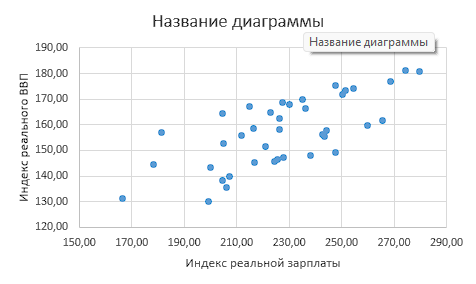
Рисунок 1
Расположение облака точек на поле корреляции произошло из левого нижнего угла в правый верхний угол. Это свидетельствует о том, что между признаками существует прямая корреляционная связь. С увеличением индекса реальной зарплаты индекс реального ВВП тоже увеличивается. По расположению точек на графике можно предположить линейную зависимость признаков.
Коэффициент корреляции.
Формула: 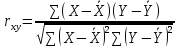
В excel: =КОРРЕЛ()
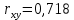
Вывод. Коэффициент корреляции (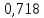 ) показывает, что связь между индексом реальной зарплаты и индексом реального ВВП высокая и прямая. ) показывает, что связь между индексом реальной зарплаты и индексом реального ВВП высокая и прямая.
Коэффициент детерминации характеризует долю вариации результативного признака под влиянием фактора, включенного в модель.
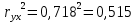
Вывод. 51,5% вариации индекса реального ВВП у происходит под влиянием индекса реальной зарплаты. Остальные 48,5% вариации индекса реального ВВП у происходит под влиянием прочих неучтенных факторов.
Выдвигаем гипотезу о равенстве нулю коэффициента корреляции (незначимости связи между признаками):
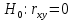
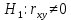
Для проверки гипотезы рассчитываем значение t-критерия Стьюдента:
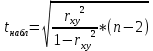 =6,37 =6,37
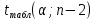 =2,02 =2,02
В excel: 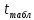 =СТЬЮДРАСПОБР ( =СТЬЮДРАСПОБР (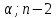 ) )
Вывод. Поскольку 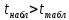 , то нулевую гипотезу о равенстве нулю коэффициента корреляции , то нулевую гипотезу о равенстве нулю коэффициента корреляции 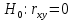 отклоняем с вероятностью допустить ошибку в 5%. Связь между индексом реальной зарплаты и индексом ВВП является статистически значимой. отклоняем с вероятностью допустить ошибку в 5%. Связь между индексом реальной зарплаты и индексом ВВП является статистически значимой.
3. Оценка параметров модели парной регрессии
Парная линейная регрессия определяется моделью вида: 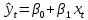
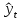 - расчетные теоретические значения результативного признака для наблюдения t; - расчетные теоретические значения результативного признака для наблюдения t;
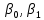 – параметры линейного уравнения парной регрессии; – параметры линейного уравнения парной регрессии;
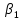 – коэффициент регрессии, который показывает на сколько в среднем изменяется значение результативного признака у при увеличении фактора х на единицу измерения. – коэффициент регрессии, который показывает на сколько в среднем изменяется значение результативного признака у при увеличении фактора х на единицу измерения.
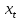 – значение факторного признака для наблюдения t. – значение факторного признака для наблюдения t.
Параметры линейного уравнения находят с помощью метода наименьших квадратов (МНК). Для этого необходимо решить систему линейных уравнений (нормальных уравнений):
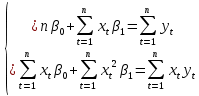
Для расчета параметров можно использовать готовые формулы, которые вытекают из этой системы:
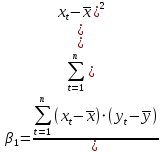
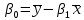
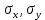 - средние квадратические отклонения признаков. - средние квадратические отклонения признаков.
Для расчета параметров модели в Excel использует надстройку Анализ данных, инструмент Регрессия (Рисунок 2).
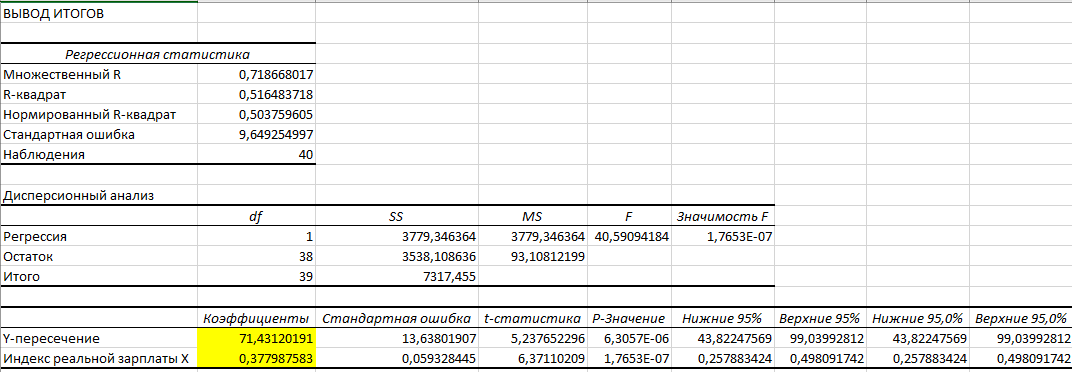
Рисунок 2
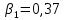
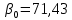
Получили линейную модель регрессии:
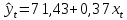
Вывод. Коэффициент регрессии β1 показывает, что при увеличении индекса реальной зарплаты на 1% по сравнению с предыдущим кварталом индекс реального ВВП в среднем увеличивается на 0,383%.
Свободный член β0оценивает влияние прочих факторов, оказывающих воздействие на результативный признак. Т.е. воздействие прочих факторов увеличивает значение индекса реального ВВП.
Свободный член показывает значение результативного признака у при значении факторного признака х = 0. Однако индекс реальной зарплаты не может быть равным нулю, поэтому данную интерпретацию свободного члена не рассматриваем.
Расчетные (теоретические, смоделированные) значения результативного показателя (индекса реального ВВП) получаем путем последовательной подстановки 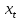 в уравнение регрессии. в уравнение регрессии.
Рассчитываем остатки (случайную компоненту, ошибку), как разность фактических и расчетных значений:
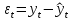
Оценка значимости модели
Выдвигаем гипотезу о том, что найденные показатели тесноты связи случайны, т.е. коэффициент детерминации равен нулю:
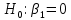
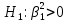
Для проверки нулевой гипотезы рассчитываем значение F-критерия Фишера:
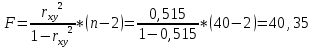
Значение в Excel 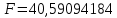
По таблице значений критерия Фишера находим табличное (критическое) значение критерия на уровне значимости α = 0,05 и с числом степеней свободы df1 = 1 и df2 = n– 2 = 40 – 2 = 38:
Fтабл = 4,08
В среде Excel для нахождения критического (табличного) значения используем функцию FРАСПОБР = 4,084745733
Вывод. Поскольку Fтабл < F, то нулевую гипотезу отклоняем. В качестве альтернативы принимаем гипотезу о том, что характеристики тесноты связи значимы, не случайны, т.е. значима построенная модель регрессии зависимости индекса ВВП от индекса реальной зарплаты.
Оценка значимости параметров модели
Выдвигаем нулевые гипотезы о том, что найденные параметры не являются статистически значимыми:
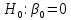 и и 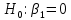
Для проверки гипотез рассчитывают t-критерий Стьюдента:
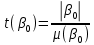 и и 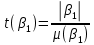 , где , где
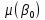 , , 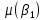 – стандартные ошибки параметров модели. – стандартные ошибки параметров модели.
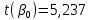
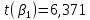
Критическое значение критерия Стьюдента находим на уровне значимости α = 0,05 и с числом степеней свободы df = n– 2 = 40 – 2 = 38:
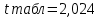
Вывод. Поскольку 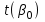 , , 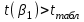 , то нулевые гипотезы отклоняем с вероятностью допустить ошибку в 5%, параметры модели являются статистически значимыми (значимо отличаются от нуля). Коэффициент регрессии β1 является статистически значимым, а, следовательно, и фактор при этом коэффициенте (индекс реальной зарплаты) статистически значим. , то нулевые гипотезы отклоняем с вероятностью допустить ошибку в 5%, параметры модели являются статистически значимыми (значимо отличаются от нуля). Коэффициент регрессии β1 является статистически значимым, а, следовательно, и фактор при этом коэффициенте (индекс реальной зарплаты) статистически значим.
Оценка точности модели
Для оценки точности модели рассчитываем среднюю относительную ошибку аппроксимации по формуле:
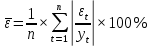
Расчет средней относительной ошибки аппроксимации:
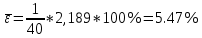
Вывод. Ошибка показывает, что в среднем фактические значения индекса реального ВВП 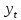 отличаются от полученных по модели регрессии отличаются от полученных по модели регрессии 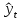 на 5,47%. Т.к. значение ошибки не превышает 7%, то модель считается точной. Т.е. построенная модель зависимости индекса реального ВВП от индекса реальной зарплаты хорошо аппроксимирует исходные данные. на 5,47%. Т.к. значение ошибки не превышает 7%, то модель считается точной. Т.е. построенная модель зависимости индекса реального ВВП от индекса реальной зарплаты хорошо аппроксимирует исходные данные.
5. Оценивание адекватности модели
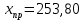
Прогнозное значение результативного признака (точечный прогноз):
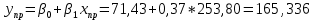
Находим стандартную ошибку модели
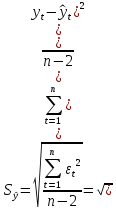
Рассчитываем ошибку прогноза:
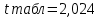
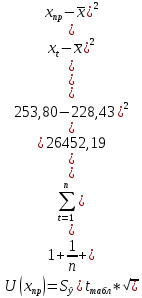
Находим нижнюю границу прогноза:
165,336 – 20 = 145,336
Находим верхнюю границу прогноза:
165,336 + 20 = 185,336
Вывод. Значение индекса ВВП будет заключено в пределах от 145,336
до 185,336.
Фактическое значение индекса ВВП в 4-м квартале 2016 года составляло 176. Фактическое значение попадает в доверительный интервал, следовательно, модель адекватна и качественно описывает взаимосвязь признаков.
6. Проверка предпосылки о гомоскедастичности остатков
Гомоскедастичность означает, что для каждого значения фактора x остатки имеют одинаковую дисперсию. В противном случае остатки являются гетероскедастичными.
Наличие гетероскедастичности можно увидеть по графику зависимости остатков 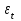 от теоретических значений результативного признака от теоретических значений результативного признака 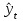 (рисунок 3). (рисунок 3).
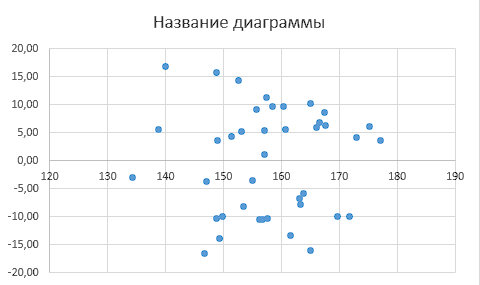
Рисунок 3
Вывод. Визуальный анализ не позволяет сделать вывод о наличии или отсутствии гетероскедастичности в остатках.
Проверим наличие гетероскедастичности с помощью теста Голдфельда-Квандта.
Ранжируем ряд в порядке возрастания фактора х.
Удалим 20% (8) центральных наблюдений. Удаляем 8 центральных наблюдений.
Делим ряд на 2 равные части (по 14 наблюдений в каждой) с малыми и большими значениями факторного признака.
Для каждой из частей находим остаточную сумму квадратов отклонений 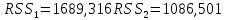
Находим эмпирическое значение F-критерия Фишера:
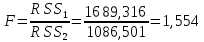
По таблице значений критерия Фишера находим табличное значение на уровне значимости α = 0,05 и с числом степеней свободы df1=n1– k – 1 = 16 – 1 – 1 = 14 и df2= n2 – k – 1 = 16 – 1 – 1 = 14:
Fтабл = 2,483
Вывод. Т.к. F = 1,554 < Fтабл = 2,483, то тест Голдфельда-Квандта обнаружения гетероскедастичности не выполняется, остатки являются гомоскедастичными, имеют постоянную дисперсию. Предпосылка выполняется, модель адекватна.
7. Проверка предпосылки об отсутствии автокорреляции случайных возмущений
Построим график зависимости значений остатков от фактора (рисунок 4).
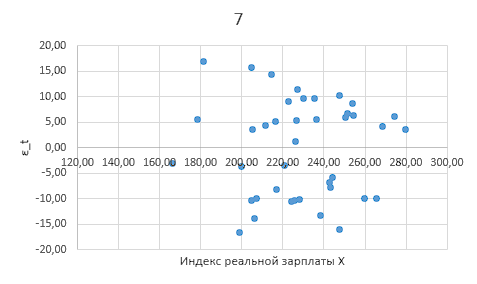
Рисунок 4
Вывод. Визуальный анализ графика остатков показывает, что распределение остатков не зависит от значений фактора, автокорреляция в ряду остатков отсутствует, предпосылка о независимости остатков выполняется.
Для проверки наличия автокорреляции применяем критерий Дарбина – Уотсона:
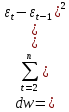
При этом данные должны быть упорядочены по фактору х.
Значение коэффициента находится в пределах от 0 до 4. В случае отсутствия автокорреляции dw = 2, при положительной автокорреляции dwстремится к нулю, а при отрицательной - к 4.
На практике применение критерия Дарбина—Уотсона основано на сравнении величины dw с теоретическими значениями d1 и d2для заданных числа наблюдений n, числа независимых переменных модели k и уровня значимости α.
1. Если dw < d1, то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция);
2. Если d2 < dw < 2, то гипотеза не отвергается;
3. Если d1 < dw< d2, то нет достаточных оснований для принятия решений.
4. Когда расчетное значение dw превышает 2, то с d1 и d2сравнивается не сам коэффициент dw, а выражение 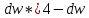 . .
Т.к. dw> 2, то находим 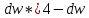 = 4 – 2,149 = 1,851 = 4 – 2,149 = 1,851
Для n= 40 при k = 1 и α = 0,05 табличные значения составляют:
d1 = 1,44 d2 = 1,54
Вывод. Т.к. 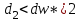 , то гипотеза о независимости остатков принимается. С вероятностью 95% можно утверждать, что предпосылка об отсутствии автокорреляции выполняется. В ряду остатков автокорреляция отсутствует. Модель адекватна. , то гипотеза о независимости остатков принимается. С вероятностью 95% можно утверждать, что предпосылка об отсутствии автокорреляции выполняется. В ряду остатков автокорреляция отсутствует. Модель адекватна.
8. Множественная регрессия
График динамики индекса реальной зарплаты (рисунок 5).
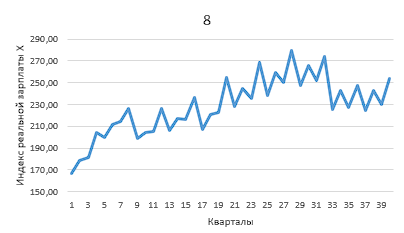
Рисунок 5
Вывод. График показывает, что динамика индекса реальной зарплаты содержит сезонную составляющую. Существенный рост индекса в 4-м квартале сменяется резким спадом в 1-м квартале. Возможно, динамика имеет незначительный тренд.
9. Построение спецификации эконометрической модели множественной регрессии.
Построим модель с учетом сезонности. Общий вид модели:
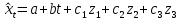 , где , где
t = 1, 2, …, 40 – порядковый номер квартала;
z1= 1 – для первого квартала;
z2= 1 – для второго квартала;
z3= 1 – для третьего квартала;
a, b, c1, c2, c3 – параметры модели.
В остальных случаях z1 = z2 = z3 = 0.
Получаем модель динамики индекса реальной зарплаты:
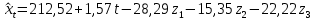
Или модели по кварталам:
Для 1-го квартала:
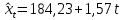
Для 2-го квартала:
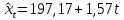
Для 3-го квартала:
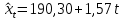
Для 4-го квартала:
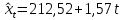
Таким образом, линии тренда для каждого квартала отличаются только свободным членом.
Оценка качества и значимости модели
1. Индекс множественной корреляции:
R = 0,847
2. Коэффициент детерминации:
R2 = 0,717
Вывод. В построенной модели тренда связь индекса реальной зарплаты с факторами (течением времени и сезонного фактора) тесная. 71,7% вариации индекса реальной зарплаты происходит под влиянием тренда и сезонности.
3. Оценка значимости модели в целом по критерию Фишера:
F = 22,21> Fтабл(α = 0,05; 4; 38) = 2,618 – модель является статистически значимой, т.е. адекватной.
4. Оценка значимости параметров модели.
Критическое (табличное значение):
tтабл(α = 0,1;38) = 1,685
Сравнение фактических значений и критического:
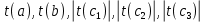 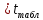 - свободный член и все коэффициенты модели являются статистически значимыми на уровне значимости α = 0,1. - свободный член и все коэффициенты модели являются статистически значимыми на уровне значимости α = 0,1.
Общий вывод. Показатели корреляции и детерминации имеют значения близкие к единице. В целом построенная модель является статистически значимой. параметры модели являются статистически значимыми с вероятностью 95%.
10. Прогнозирование экзогенной переменной - индекса реальной зарплаты.
Прогноз индекса реальной зарплаты на ближайший квартал, т.е. на 1-й квартал 2017 года (t = 41, z1 = 1):
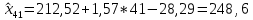
Вывод. По построенной многофакторной модели можно ожидать, что в 1-м квартале 2017 года индекс реальной зарплаты составит 248,6 к предыдущему кварталу.
11. Прогнозирование эндогенной переменной - индекса реального ВВП
Прогноз индекса реального ВВП по линейной модели парной регрессии:
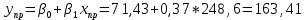
Рассчитываем среднюю квадратическую ошибку прогноза:
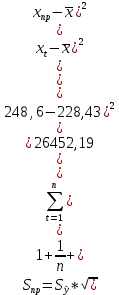
По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости α = 0,1 и с числом степеней свободы df = n– 2 = 40 – 2 = 38:
=СТЬЮДРАСПОБР(0,1;38)
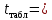 1,685 1,685
Рассчитываем ширину доверительного интервала:
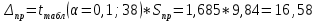
Находим нижнюю границу прогноза:
163,41– 16,58 = 146,83
Находим верхнюю границу прогноза:
163,41+ 16,58= 179,99
Вывод. С вероятность 90% можно утверждать, что в 1-м квартале 2017 года индекс реального ВВП будет находится в пределах от 146,83 до 179.99.
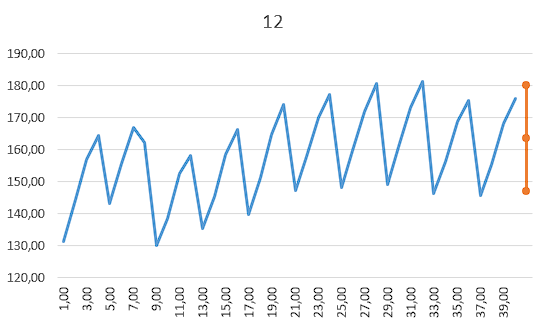
Рисунок 6 |
|
|
 Скачать 165.99 Kb.
Скачать 165.99 Kb.