|
|
Криптографическая защита информации. Ведение Криптографическая защита информации
Предыстория
В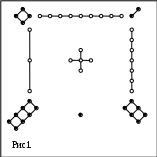 китайской древней книге «Же-ким» («Книга перестановок») приводится легенда о том, что император Ню, живший 4 тысячи лет назад, увидел на берегу реки священную черепаху. На ее панцире был изображен рисунок из белых и черных кружков (рис. 1). Если изменить каждую фигуру число, показывающим, сколько в ней кружков, получится такая таблица: китайской древней книге «Же-ким» («Книга перестановок») приводится легенда о том, что император Ню, живший 4 тысячи лет назад, увидел на берегу реки священную черепаху. На ее панцире был изображен рисунок из белых и черных кружков (рис. 1). Если изменить каждую фигуру число, показывающим, сколько в ней кружков, получится такая таблица:
У этой таблице есть замечательное свойство. Сложи числа первого столбца: 4+3+8=15. Тот же результат получится при сложении чисел второго, а также третьего столбцов. Он же получается при сложении чисел любой из трех строк. Мало этого, тот же ответ 15 получается, если сложить числа каждой из двух диагоналей: 4+5+6=8+5+2=15.
Наверное, эту легенду китайцы придумали, когда нашли расположение чисел от 1 до 9 со столь замечательным свойством. Рисунок они назвали «ло-шу» и стали считать его магическим символом и употреблять при заклинаниях. Поэтому сейчас любую квадратную таблицу, составленную из чисел и обладающую таким свойством, называют магическим квадратом.
Каким же образом составляют магические квадраты? Магический квадрат «ло-шу» можно найти, не прибегая к перебору одной за другой всех расстановок 9 цифр в 9 клетках (число таких расстановок 362 880). Будем рассуждать так. Сумма всех чисел от 1 до 9 равна: 1+2+3+4+5+6+7+8+9=45. Значит, в каждой строке и в каждом столбце сумма чисел должна равняться: 45:3=15. Но если просуммировать все числа во вторых столбце и строке и в обеих диагоналях, то каждое число войдет один раз, за исключением центрального, которое войдет четырежды. Значит, если обозначить центральное число через х, то должно выполняться равенство 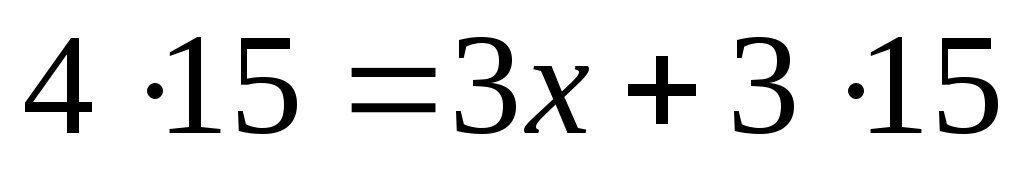 . Отсюда х=5, то есть в центре таблицы должно стоять число 5. . Отсюда х=5, то есть в центре таблицы должно стоять число 5.
Теперь заметим, что число 9 не может стоять в углу таблицы, скажем в левом верхнем. Ведь тогда в противоположном углу стояло бы число 1, а на первые строку и столбец оставалось бы одна комбинация – числа 4 и 2. Значит, 9 стоит в середине каких-то крайних строк или столбцов (у нас в середине первой строки). Двумя другими числами этой строки являются 4 и 2, а третьим числом среднего столбца должно быть 15–9–5=1. В одной строке с 1 должны стоять числа 8 и 6. Тем самым магический квадрат почти заполнен и легко найти место для оставшихся чисел. В результате получается квадрат «ло-шу». Конечно, для 9 можно выбрать другие 3 места, а после выбора места для этого числа остаются две возможности для расположения чисел 4 и 2. Всего получается 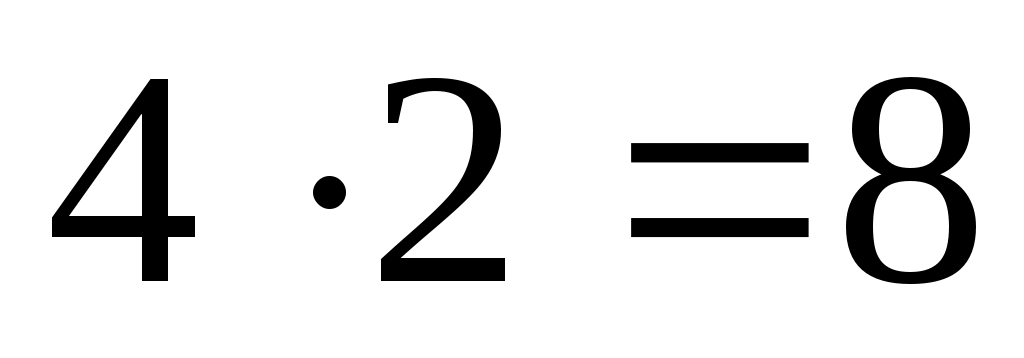 различных магических квадратов из трех строк и трех столбцов (или, как говорят математики, квадратов третьего порядка). Все эти квадраты можно получить из «ло-шу», либо поворачивая квадрат вокруг центра на различных магических квадратов из трех строк и трех столбцов (или, как говорят математики, квадратов третьего порядка). Все эти квадраты можно получить из «ло-шу», либо поворачивая квадрат вокруг центра на  , , 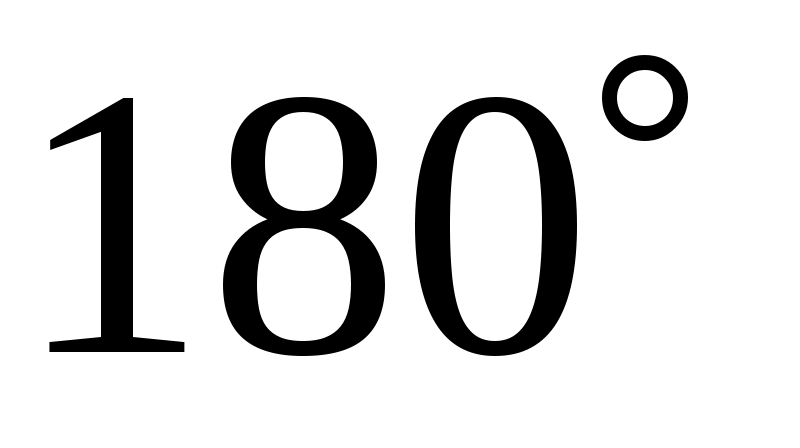 или или 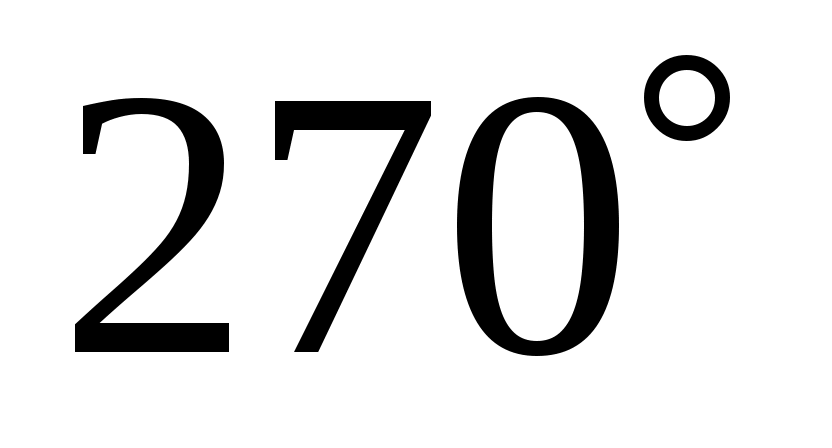 , либо зеркально отражая его. , либо зеркально отражая его.
Вообще, если уже найден какой-нибудь магический квадрат, то из него можно описанными выше методами (поворачивая и зеркальными отражениями) получить еще 7 магических квадратов. Но как же найти хоть один магический квадрат? Для квадратов не четного порядка есть совсем простой способ, он заключается в следующем. Берем средний столбец и в его верхней клетке пишем число 1. Это же число пишем ниже самой нижней клетки среднего столбца и от него начинаем писать числа 2, 3, …, идя вверх и в право (нижнее число 1 находится вне квадрата). Это делаем до тех пор, пока не дойдем до самого правого столбца. Тогда последнее написанное число записываем в той же строке слева от квадрата и идем от него вправо вверх, записывая числа в порядке возрастания. Когда дойдем до числа, за которым идет ранее написанное число 1, опускаемся на одну клетку вниз, записываем в ней следующие по порядку число и снова пишем числа в порядке возрастания так же, как и раньше. Получился квадрат пятого порядка:
|
17
|
24
|
1
|
8
|
15
|
16
|
23
|
5
|
7
|
14
|
16
|
22
|
4
|
6
|
13
|
20
|
22
|
3
|
10
|
12
|
19
|
21
|
3
|
9
|
11
|
18
|
25
|
2
|
9
|
|
17
|
24
|
1
|
8
|
|
Несложно написать и магический квадрат четвертого порядка: для этого запишем числа от 1 до 16 в квадрат по порядку. А теперь поменяем местами числа, стоящие в противоположных углах всего квадрата и внутреннего квадратика:
16
|
2
|
3
|
13
|
5
|
11
|
10
|
8
|
9
|
7
|
6
|
12
|
4
|
14
|
15
|
1
|
Описание логической структуры
Для шифрования текста методом магического квадрата нечетного порядка NxN, выполним следующие действия:
вводим исходный текст;
убираем пробелы в тексте и преобразуем строчные буквы в прописные;
определяем количество знаков в тексте MT;
вычисляем размер магического квадрата (массива):
N=MT1/2;
если N – натуральное число, тогда N=N+1;
если N2
разбиваем текст в одномерный массив и в пустые значения присваиваем “*”
определяем среднее значение массива Sr=N/2 и округляем её до целого числа;
приравниваем i=1, j=Sr;
в цикле по k от 1 до N2 с шагом равной 1:
приравниваем i=i+2, j=j-1, если i<1 и j>N, не-то i=N, если i<1, не-то j=1, если j>N, не-то i=i+2, j=j-1, если Mi,j>0;
Формируем магический квадрат Mi,j=k;
выводим размер магического квадрата
выводи магический квадрат;
распределяем текст в магический квадрат и выводим текст в матрице
выводим шифрованный текст.
Блок-схема для метода шифрования магическим квадратом (создание магического квадрата из цифр):
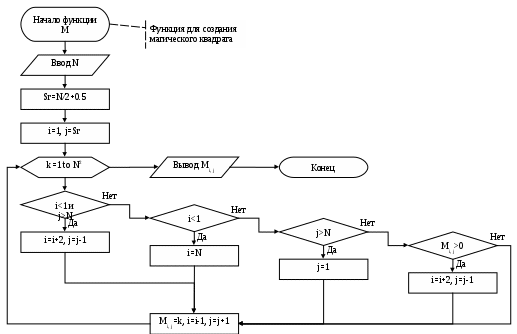
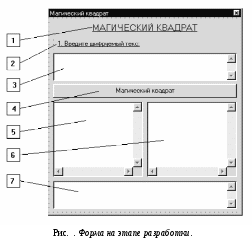
Объекты CODEMAGSQ.FRM и значения их свойств
| |
|
|
Тип и номер1
|
Свойство
|
Значение
|
Form
|
|
|
|
Name
|
frmCodeMagSq
|
|
BorderStyle
|
4 – Fixed ToolWindows
|
|
Caption
|
Магический квадрат
|
|
MaxButton
|
0 – False
|
|
MDIChild
|
-1 – True
|
|
MinButton
|
0 – False
|
|
ShowInTaskbar
|
0 – False
|
Label
|
|
|
1
|
Name
|
LabTitle
|
|
Alignment
|
2 – Center
|
|
Caption
|
МАГИЧЕСКИЙ КВАДРАТ
|
|
Font
|
|
|
|
Underline
|
-1 – True
|
Label
|
|
|
2
|
Name
|
Lab1
|
|
Caption
|
1. Введите шифруемый текс:
|
|
Font
|
|
|
|
Underline
|
-1 – True
|
TextBox
|
|
|
3
|
Name
|
txtEntrance
|
|
MultiLine
|
-1 – True
|
|
ScrollBars
|
2 – Vertical
|
CommandButton
|
|
|
4
|
Name
|
cmdCodeMagSq
|
|
Caption
|
Магический квадрат
|
TextBox
|
|
|
5
|
Name
|
txtMagSqInNum
|
|
MultiLine
|
-1 – True
|
|
ScrollBars
|
3 – Both
|
TextBox
|
|
|
6
|
Name
|
txtTextInMagSq
|
|
MultiLine
|
-1 – True
|
|
ScrollBars
|
3 – Both
|
TextBox
|
|
|
7
|
Name
|
txtCodeMagSq
|
|
MultiLine
|
-1 – True
|
|
ScrollBars
|
2 – Vertical
|
1 Номер указанный в первой колонке, соответствует порядковому номеру объекта на форме (рис. )
|
Исходный код CODEMAGSQ.FRM
|
Option Explicit
Private Sub cmdCodeMagSq_Click()
'Описание переменных
Dim intMagSqInNum() As Integer 'Магический квадрат в числах
Dim strTextInMagSq() As String 'Текст в магическом квадрате
Dim strTextInArray() As String 'Одномерный массив шифруемого текста
Dim intSizeOfArray As Integer 'Размер массива
Dim i%, j% 'Integer(%)
Dim strTextWBlanks As String 'Текст без пробелов
Dim lngMarksInText As Long 'Чило знаков в тексте
'Убираем пробелы в тексте
'и преобразуем строчные буквы в прописные
strTextWBlanks = StrConv(Replace(txtEntrance.Text, " ", ""), vbUpperCase)
'Вычисляем колличество знаков в тексте
lngMarksInText = Len(strTextWBlanks)
'Вычисляем размер магического квадрата (массива)
intSizeOfArray = Int(Sqr(lngMarksInText))
If intSizeOfArray Mod 2 = 0 Then intSizeOfArray = intSizeOfArray + 1
If intSizeOfArray ^ 2 < lngMarksInText Then intSizeOfArray = intSizeOfArray + 2
'Разбиваем текс в одномерный массив
'и в пустые значения присваеваем "*"
ReDim strTextInArray(intSizeOfArray ^ 2)
For i = 1 To intSizeOfArray ^ 2
If i > CInt(lngMarksInText) Then
strTextInArray(i) = "*"
Else
strTextInArray(i) = Mid(strTextWBlanks, i, 1)
End If
Next i
'Создаем магический квадрат с помощью функции MagSqInNum
intMagSqInNum = MagSqInNum(intSizeOfArray)
'Выводим магический квадрат
txtMagSqInNum.Text = ""
For i = 1 To intSizeOfArray
For j = 1 To intSizeOfArray
txtMagSqInNum.Text = txtMagSqInNum.Text & intMagSqInNum(i, j) & " "
Next j
txtMagSqInNum.Text = txtMagSqInNum.Text & vbCrLf
Next i
'Распределяем текст в магический квадрат
'и выводим текст в матрице
ReDim strTextInMagSq(intSizeOfArray, intSizeOfArray)
txtTextInMagSq.Text = ""
For i = 1 To intSizeOfArray
For j = 1 To intSizeOfArray
strTextInMagSq(i, j) = strTextInArray(intMagSqInNum(i, j))
txtTextInMagSq.Text = txtTextInMagSq.Text & strTextInMagSq(i, j) & " "
Next j
txtTextInMagSq.Text = txtTextInMagSq.Text & vbCrLf
Next i
'Выводим шифрованный текст
txtCodeMagSq.Text = ""
For i = 1 To intSizeOfArray
For j = 1 To intSizeOfArray
strTextInMagSq(i, j) = strTextInArray(intMagSqInNum(i, j))
txtCodeMagSq.Text = txtCodeMagSq.Text & strTextInMagSq(i, j)
Next j
Next i
'Выводим размер квадрата на кнопку
cmdCodeMagSq.Caption = "Магический квадрат (" & intSizeOfArray & " x " & intSizeOfArray & ")"
End Sub
Function MagSqInNum(intSizeOfArray As Integer) As Integer()
'Функция для создания магического квадрата
'нечетного порядка NxN
'Описание переменных
Dim intMagSqInNum() As Integer 'Магический квадрат в числах
Dim intAverArray As Integer 'Среднее значение массива
Dim i%, j%, k% 'Integer(%)
Dim intVariantSq As Integer 'Вариант магического квадрата
'Определяем среднее значение массива
intAverArray = Int(intSizeOfArray / 2) + 1
'Переопределяем размер массива (квадрата)
ReDim intMagSqInNum(intSizeOfArray, intSizeOfArray)
'Выбираем вариант с помощью генератора случайных чисел
Randomize
intVariantSq = Int((8 - 1 + 1) * Rnd + 1)
'Создаем магический квадрат соответственно варианту
Select Case intVariantSq
Case Is = 1
' 8 1 6
' 3 5 7
' 4 9 2
i = 1: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i < 1 And j > intSizeOfArray Then
i = i + 2: j = j - 1
ElseIf i < 1 Then
i = intSizeOfArray
ElseIf j > intSizeOfArray Then
j = 1
ElseIf intMagSqInNum(i, j) > 0 Then
i = i + 2: j = j - 1
End If
intMagSqInNum(i, j) = k
i = i - 1: j = j + 1
Next k
Case Is = 2
' 6 7 2
' 1 5 9
' 8 3 4
i = 1: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i < 1 And j < 1 Then
i = i + 2: j = j + 1
ElseIf i < 1 Then
i = intSizeOfArray
ElseIf j < 1 Then
j = intSizeOfArray
ElseIf intMagSqInNum(j, i) > 0 Then
i = i + 2: j = j + 1
End If
intMagSqInNum(j, i) = k
i = i - 1: j = j - 1
Next k
Case Is = 3
' 2 9 4
' 7 5 3
' 6 1 8
i = intSizeOfArray: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i > intSizeOfArray And j < 1 Then
i = i - 2: j = j + 1
ElseIf i > intSizeOfArray Then
i = 1
ElseIf j < 1 Then
j = intSizeOfArray
ElseIf intMagSqInNum(i, j) > 0 Then
i = i - 2: j = j + 1
End If
intMagSqInNum(i, j) = k
i = i + 1: j = j - 1
Next k
Case Is = 4
' 4 3 8
' 9 5 1
' 2 7 6
i = intAverArray: j = intSizeOfArray
For k = 1 To intSizeOfArray ^ 2
If i > intSizeOfArray And j > intSizeOfArray Then
i = i - 1: j = j - 2
ElseIf i > intSizeOfArray Then
i = 1
ElseIf j > intSizeOfArray Then
j = 1
ElseIf intMagSqInNum(i, j) > 0 Then
i = i - 1: j = j - 2
End If
intMagSqInNum(i, j) = k
i = i + 1: j = j + 1
Next k
Case Is = 5
' 6 1 8
' 7 5 3
' 2 9 4
i = 1: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i < 1 And j < 1 Then
i = i + 2: j = j + 1
ElseIf i < 1 Then
i = intSizeOfArray
ElseIf j < 1 Then
j = intSizeOfArray
ElseIf intMagSqInNum(i, j) > 0 Then
i = i + 2: j = j + 1
End If
intMagSqInNum(i, j) = k
i = i - 1: j = j - 1
Next k
Case Is = 6
' 8 3 4
' 1 5 9
' 6 7 2
i = 1: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i < 1 And j > intSizeOfArray Then
i = i + 2: j = j - 1
ElseIf i < 1 Then
i = intSizeOfArray
ElseIf j > intSizeOfArray Then
j = 1
ElseIf intMagSqInNum(j, i) > 0 Then
i = i + 2: j = j - 1
End If
intMagSqInNum(j, i) = k
i = i - 1: j = j + 1
Next k
Case Is = 7
' 4 9 2
' 3 5 7
' 8 1 6
i = intAverArray: j = intSizeOfArray
For k = 1 To intSizeOfArray ^ 2
If i > intSizeOfArray And j > intSizeOfArray Then
i = i - 1: j = j - 2
ElseIf i > intSizeOfArray Then
i = 1
ElseIf j > intSizeOfArray Then
j = 1
ElseIf intMagSqInNum(j, i) > 0 Then
i = i - 1: j = j - 2
End If
intMagSqInNum(j, i) = k
i = i + 1: j = j + 1
Next k
Case Is = 8
' 2 7 6
' 9 5 1
' 4 3 8
i = intSizeOfArray: j = intAverArray
For k = 1 To intSizeOfArray ^ 2
If i > intSizeOfArray And j < 1 Then
i = i - 2: j = j + 1
ElseIf i > intSizeOfArray Then
i = 1
ElseIf j < 1 Then
j = intSizeOfArray
ElseIf intMagSqInNum(j, i) > 0 Then
i = i - 2: j = j + 1
End If
intMagSqInNum(j, i) = k
i = i + 1: j = j - 1
Next k
End Select
MagSqInNum = intMagSqInNum
End Function
|
Входной данной является шифруемый текст.
Выходными данными являются сам магический квадрат, его размер, магический квадрат из букв и шифрованный текст.
|
|
|
 Скачать 0.84 Mb.
Скачать 0.84 Mb. китайской древней книге «Же-ким» («Книга перестановок») приводится легенда о том, что император Ню, живший 4 тысячи лет назад, увидел на берегу реки священную черепаху. На ее панцире был изображен рисунок из белых и черных кружков (рис. 1). Если изменить каждую фигуру число, показывающим, сколько в ней кружков, получится такая таблица:
китайской древней книге «Же-ким» («Книга перестановок») приводится легенда о том, что император Ню, живший 4 тысячи лет назад, увидел на берегу реки священную черепаху. На ее панцире был изображен рисунок из белых и черных кружков (рис. 1). Если изменить каждую фигуру число, показывающим, сколько в ней кружков, получится такая таблица:


