Криптографическая защита информации. Ведение Криптографическая защита информации

• Название: Ведение Криптографическая защита информации
• Анкор: Криптографическая защита информации
• Дата: 25.12.2021
• Размер: 0.84 Mb.
• Имя файла: Криптографическая защита информации.doc
• Тип: Документы; #317994
• страница: 6 из 6

Шифрование методом гаммирования

Описание задачи

Суть этого метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, которая называется гаммой. Иногда такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название "гаммирование".

Процедуру наложения гаммы на исходный текст можно осуществить двумя способами. При первом способе символы исходного текста и гаммы заменяются цифровыми эквивалентами, которые затем складываются по модулю k, где k – число символов в алфавите, т.е.

Т_ш = (Т_о + Т_г) mod k,

где T_ш, T_о, T_г – символы соответственно зашифрованного, исходного текста и гаммы.

При втором методе символы исходного текста и гаммы представляются в виде двоичного кода, затем соответствующие разряды складываются по модулю 2. Вместо сложения по модулю 2 при гаммировании можно использовать и другие логические операции, например преобразование по правилу логической эквивалентности или логической неэквивалентности.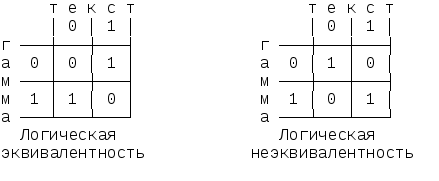

Такая замена равносильна введению еще одного ключа, которым является выбор правила формирования символов зашифрованного сообщения из символов исходного текста и гаммы.

Стойкость шифрования методом гаммирования определяется главным образом свойствами гаммы – длительностью периода и равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода.

Обычно разделяют две разновидности гаммирования – с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длиной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой шифр теоретически является абсолютно стойким, т.е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста. Это, однако, не означает, что дешифрование такого текста вообще невозможно: при наличии некоторой дополнительной информации исходный текст может быть частично или полностью восстановлен даже при использовании бесконечной гаммы.

В качестве гаммы может быть использована любая последовательность случайных символов, например, последовательность цифр числа пи, числа е и т.п. При шифровании с помощью ЭВМ последовательность гаммы формируется с помощью датчика псевдослучайных чисел. В настоящее время разработано несколько алгоритмов работы таких датчиков, которые обеспечивают удовлетворительные характеристики гаммы.

Описание логической структуры

#include

#include

#include
unsigned char otext[255];

unsigned char ztext[255];
void main()

{

unsigned i;

unsigned char key;

clrscr();

for (i=0; i<255; i++)

{

otext[i]=0;

ztext[i]=0;

};

printf("Введите английский текст: ");

i=0;

do

{

key=bioskey(0);

if (key==32)

{

otext[i]='*';

printf("%c",key);

i++;

};

key=key & 0xDF;

if (key==32)

{

otext[i]='*';

printf("%c",key);

i++;

};

if (key!=13)

if ((key>'@') && (key<'['))

{

otext[i]=key;

printf("%c",key);

i++;

};

}

while ((i<255) && (key!=13));

i=0;

do

{

if (otext[i]!=0)

{

ztext[i]=otext[i] ^ 0x69;

i++;

};

}

while (otext[i]!=0);

printf("\nЗашифрованный текст: ");

i=0;

do

{

if (ztext[i]!=0)

printf("%c",ztext[i]);

else i=254;

i++;

}
while (i<255);

bioskey(0);

7. Шифрование с помощью аналитических преобразований

Описание задачи

Достаточно надежное закрытие информации может быть обеспечено при использовании для шифрования некоторых аналитических преобразований. Для этого можно использовать методы алгебры матриц, например, умножение матрицы на вектор по правилу:

.

Если матрицу |A_ij| использовать в качестве ключа, а вместо компонента вектора В_j подставить символы исходного текста, то компоненты вектора C_j будут представлять собой символы зашифрованного текста.

Приведем пример использования такого метода, взяв в качестве ключа квадратную матрицу третьего порядка



Заменим буквы алфавита цифрами, соответствующими их порядковому номеру в алфавите: А - 0, Б - 1, В - 3, и т.д. Тогда отрывку текста "ВАТАЛА" (текст взят произвольно) будет соответствовать последовательность 3, 0, 19, 0, 12, 0. По принятому алгоритму шифрования выполним необходимые действия: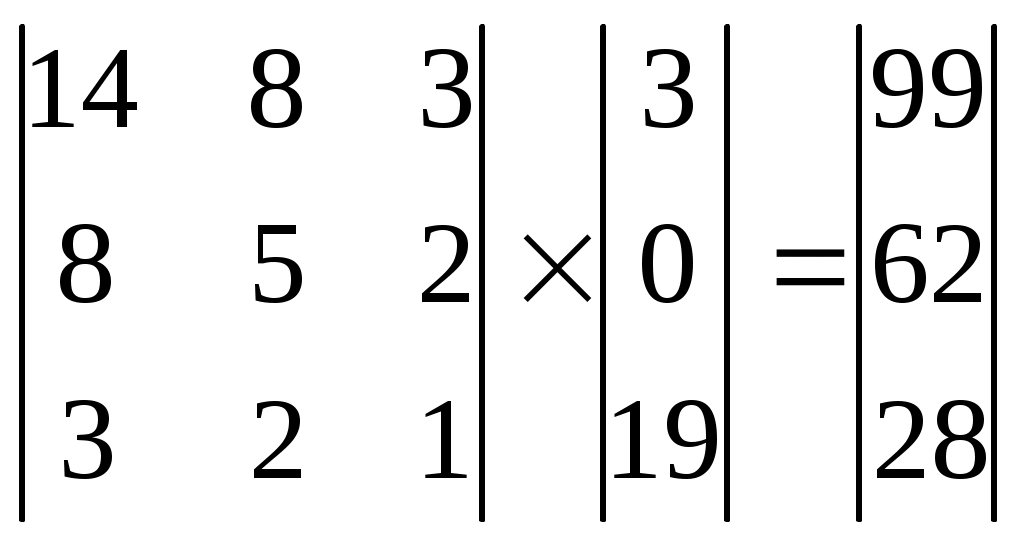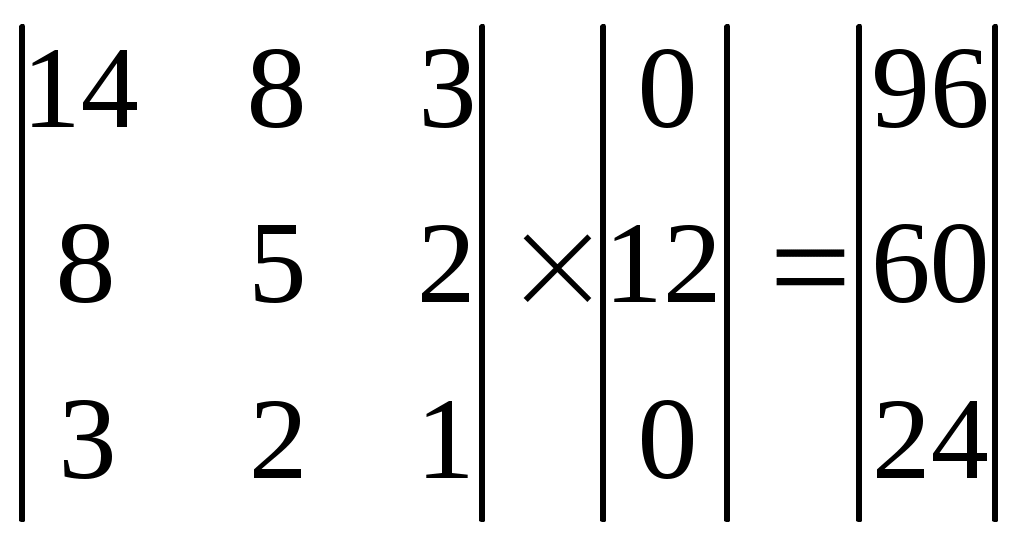





При этом зашифрованный текст будет иметь вид:

99, 62, 28, 96, 60, 24.

Расшифрование осуществляется с использованием того же правила умножения матриц на вектор, только в качестве основы берется матрица, обратная той, с помощью которой осуществляется закрытие, а в качестве вектора-сомножителя – соответствующее количество символов закрытого текста; тогда значениями вектора-результата будут цифровые эквиваленты знаков открытого текста.

Обратной к данной, как известно, называется матрица, получающаяся из так называемой присоединенной матрицы делением всех ее элементов на определитель данной матрицы. В свою очередь присоединенной называется матрица, составленная из алгебраических дополнений А, к элементам данной матрицы, которые вычисляются по формуле:

,

где D_ij – определитель матрицы, получаемый вычеркиванием i^-ой ее строки и j^-го столбца.

Определителем же, как известно, называется алгебраическая сумма n! членов (для определителя n^-го порядка), составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член суммы берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае. Для матрицы третьего порядка, например, определитель вычисляется по следующей формуле:



Вычисленная по данной формуле матрица, обратная к принятой нами за основу для закрытия, будет иметь вид: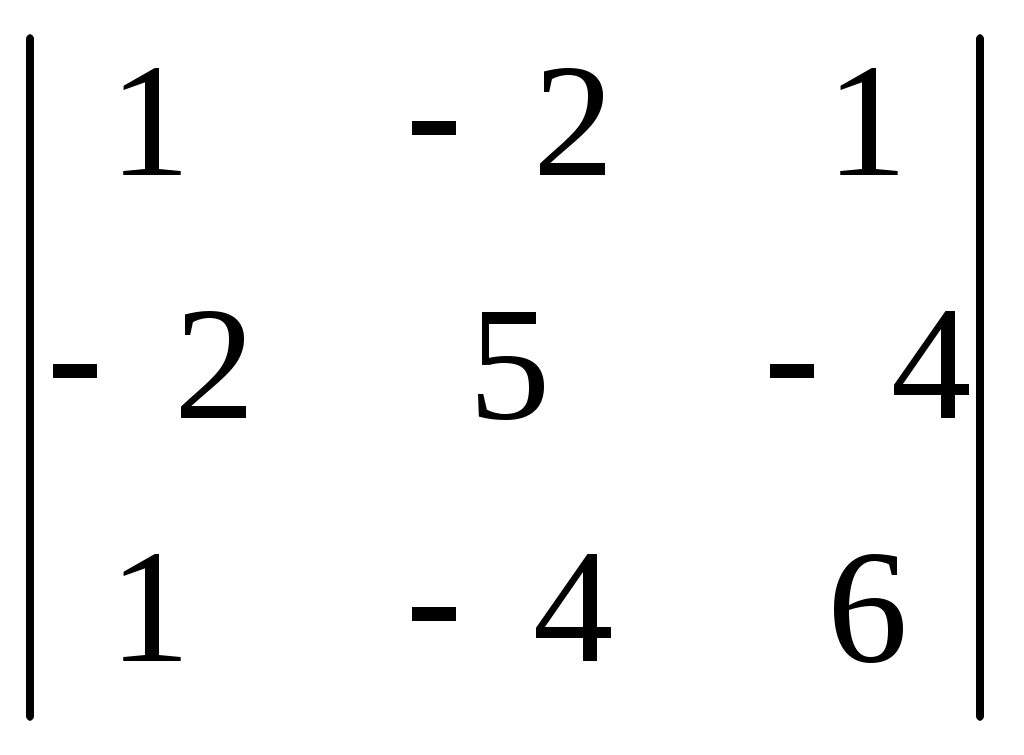



Тогда в условиях нашего примера процесс раскрытия будет выглядеть так: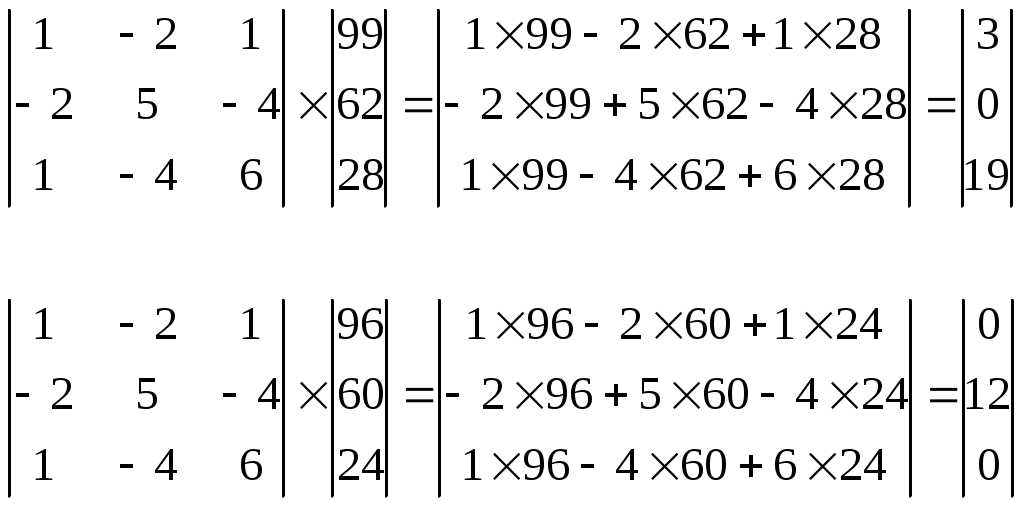



Таким образом, получили следующую последовательность знаков раскрытого текста: 3, 0, 19, 0, 12, 0, что соответствует исходному тексту. Нетрудно видеть, что и этот метод шифрования является формализованным, что позволяет легко реализовать его программными средствами.

Описание логической структуры

Для шифрования текста с помощью аналитических преобразований, выполним следующие действия:

• 
  Вводим шифруемый текст;
  
• 
  Создаем ключ;
  
• 
  Вычисляем количество знаков в тексте;
  
• 
  Вычисляем, какое количество раз будем обращаться к ключу;
  
• 
  Преобразуем шифруемый текст в байтовый массив;
  
• 
  Выводим шифрованный текст (код).
  

Объекты CODEANALIT.FRM и значения их свойств
Тип и номер1	Свойство			Значение
Form
	Name			FrmCodeAnalit
	BorderStyle			4 – Fixed ToolWindows
	Caption			Аналитическое преобразование
	MaxButton			0 – False
	MDIChild			-1 – True
	MinButton			0 – False
	ShowInTaskbar			0 – False
Label
1	Name			LabTitle
	Alignment			2 – Center
	Caption			ШИФРОВАНИЕ С ПОМОШЬЮ АНАЛИТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
	Font
			Underline	-1 – True
Label
2	Name			lblEntrance
	Caption			1. Введите шифруемый текст.
	Font
			Underline	-1 – True
TextBox
3	Name			txtEntrance
	Alignment			2 – Center
	Font
		Name		Courier New
CommandButton
4	Name			cmdCodeAnalit
	Caption			Аналитичекское преобразование
Label
5	Name			lblCodeAnalit
	Caption			Шифрованный текст:
	Font
		Underline		-1 – True
TextBox
6	Name			txtCodeAnalit
	Alignment			2 – Center
1 Номер указанный в первой колонке, соответствует порядковому номеру объекта на форме (рис. )

Исходный код CODEANALIT.FRM

Option Explicit Private Sub cmdCodeAnalit_Click() 'Описываем переменные Dim varKeyText() As Variant 'Ключ в одномерном массиве Dim intSizeOfArray As Integer 'Размер массива Dim intKey() As Integer 'Ключ распределенный в квадратный массив Dim strEntranceText As String 'Шифруемый текст Dim intMarksInText As Integer 'Число знаков в тексте Dim bytTextInByteArray() As Byte 'Текст в байтовом массиве Dim intReferenceToKey As Integer ' Кол-во общений к ключу Dim strCodeAnalit As String 'Шифрованный текст Dim i%, j%, k%, n%, sum% 'Вспомогательные переменные (%-As Integer) 'Вводим шифруемый текст strEntranceText = txtEntrance.Text 'Создаем ключ varKeyText = Array(14, 8, 3, 8, 5, 2, 3, 2, 1) intSizeOfArray = 3 ReDim intKey(intSizeOfArray, intSizeOfArray) k = 0 For i = 1 To intSizeOfArray For j = 1 To intSizeOfArray intKey(i, j) = varKeyText(k) k = k + 1 Next j Next i 'Вычисляем колличество знаков в тексте intMarksInText = CInt(Len(strEntranceText)) 'Вычмсляем, какое кол-во раз 'будем обращатся к ключу Do While intMarksInText Mod intSizeOfArray <> 0 intMarksInText = intMarksInText + 1 strEntranceText = strEntranceText & " " Loop intReferenceToKey = intMarksInText / intSizeOfArray - 1 'Преобразуем шифруемый текст в байтовый массив bytTextInByteArray() = StrConv(strEntranceText, vbFromUnicode) 'Шифруем текст For n = 0 To intReferenceToKey For i = 1 To intSizeOfArray k = n * intSizeOfArray sum = 0 For j = 1 To intSizeOfArray sum = sum + intKey(i, j) * bytTextInByteArray(k) k = k + 1 Next j strCodeAnalit = strCodeAnalit & sum & " " Next i Next n 'Выводим шифрованный текст (код) txtCodeAnalit.Text = strCodeAnalit End Sub

В ходные и выходные данные

Входными данными являются 30 буквенный алфавит, ключ и шифруемый текст.

Выходными данными являются перемешанный алфавит, текст в виде последовательности биграмм, шифр текст и шифр текст без пробелов.