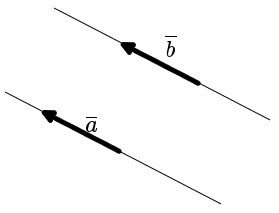
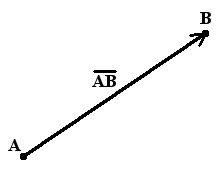
векторы. векторы задачи. Вектор это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало точка

• Название: Вектор это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало точка
• Анкор: векторы
• Дата: 17.05.2021
• Размер: 1.24 Mb.
• Имя файла: векторы задачи.doc
• Тип: Документы; #206137

Вектор - это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало - точка. Модуль вектора (абсолютная величина) - длина этого направленного отрезка.

Если начало вектора совпадает с его концом, получим нулевой вектор.

Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.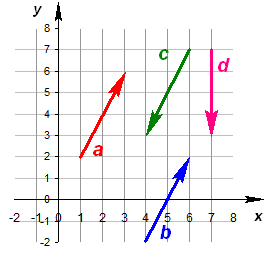



Длина вектора

Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

Нулевой вектор

Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.

Нулевой вектор обычно обозначается как 0.

Длина нулевого вектора равна нулю.

Равные вектора

Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).

рис. 6

Условие равенства векторов. Вектора равны, если их координаты равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b, если a↑↑b и |a| = |b|.

Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.

Решение:

a = b - так как их координаты равны,
a ≠ c - так как их координаты не равны,
b ≠ c - так как их координаты не равны.

Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.

Решение:

a = c - так как их координаты равны,
a ≠ b - так как их координаты не равны,
b ≠ c - так как их координаты не равны.

Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Единичный вектор

Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Определение длины вектора

Определение.

 Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y²

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y² + a_z²

Примеры вычисления длины вектора для плоских задачи

Пример 1. Найти длину вектора a = {2; 4}.

Решение: |a| = √2² + 4² = √4 + 16 = √20 = 2√5.

Пример 2. Найти длину вектора a = {3; -4}.

Решение: |a| = √3² + (-4)² = √9 + 16 = √25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Пример 3. Найти длину вектора a = {2; 4; 4}.

Решение: |a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Пример 4. Найти длину вектора a = {-1; 0; -3}.

Решение: |a| = √(-1)² + 0² + (-3)² = √1 + 0 + 9 = √10.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Пример 5. Найти длину вектора a = {1; -3; 3; -1}.

Решение: |a| = √1² + (-3)² + 3² + (-1)² = √1 + 9 + 9 + 1 = √20 = 2√5

Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.

Решение: |a| = √2² + 4² + 4² + 6² + 2² = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.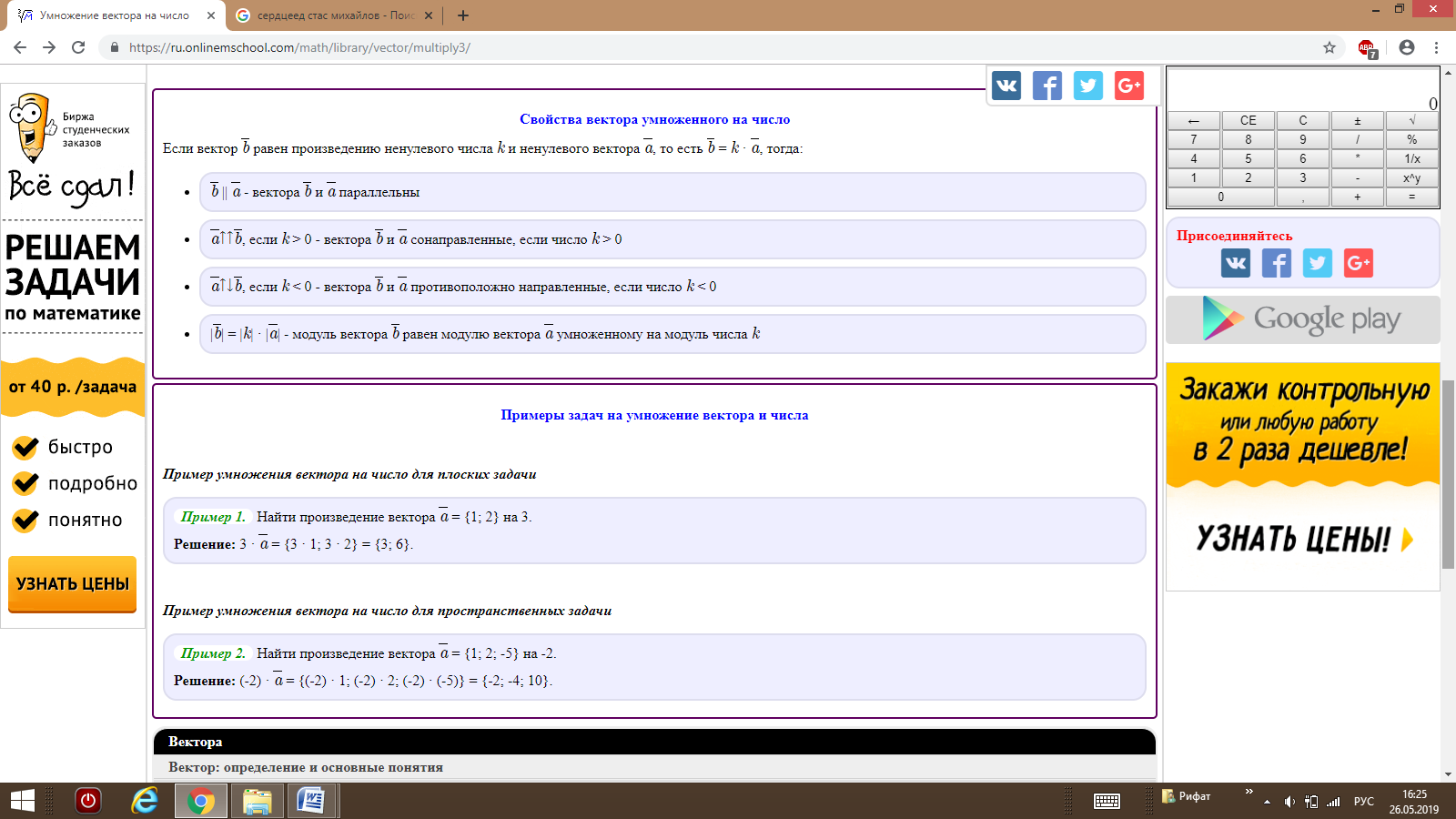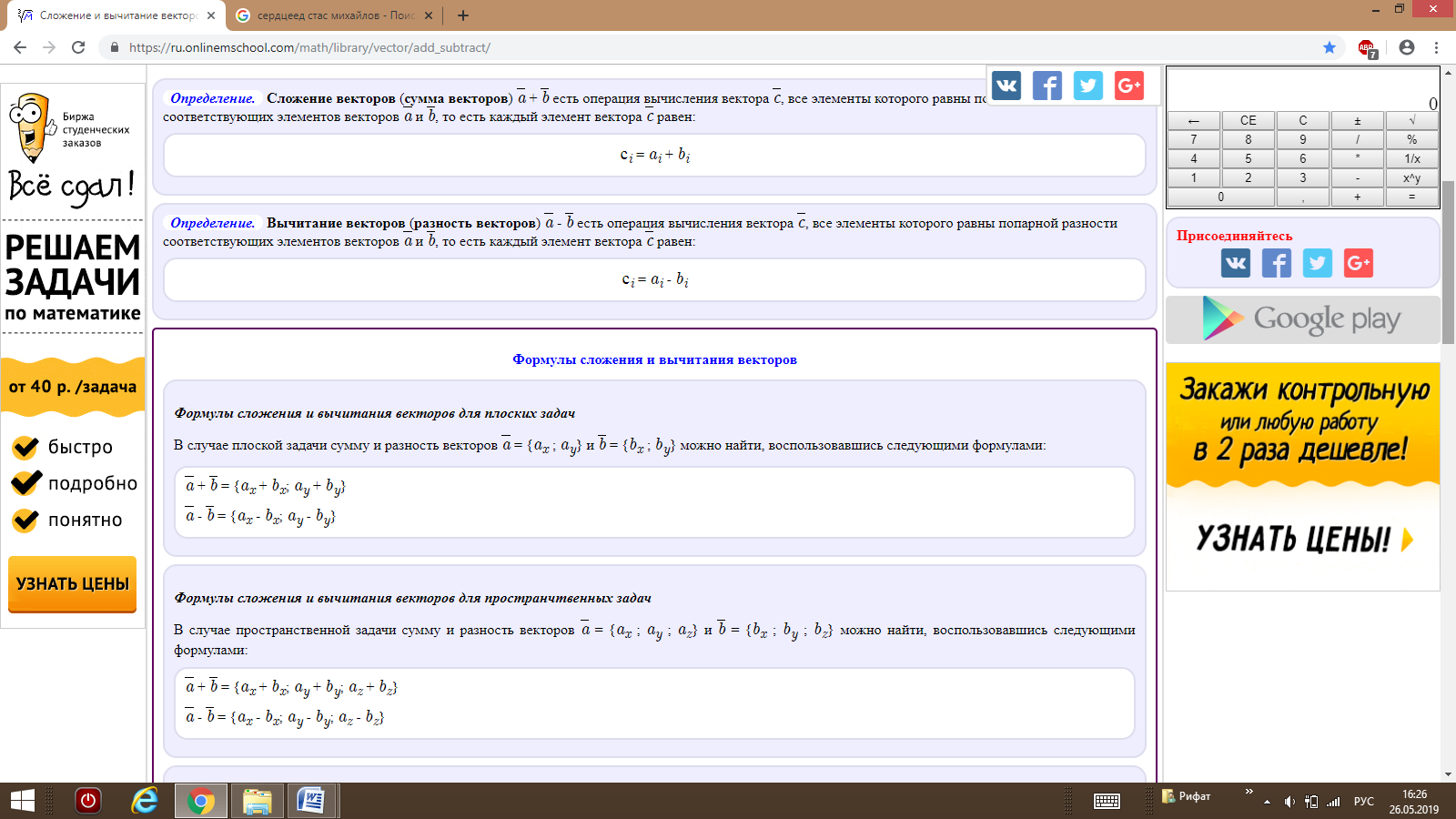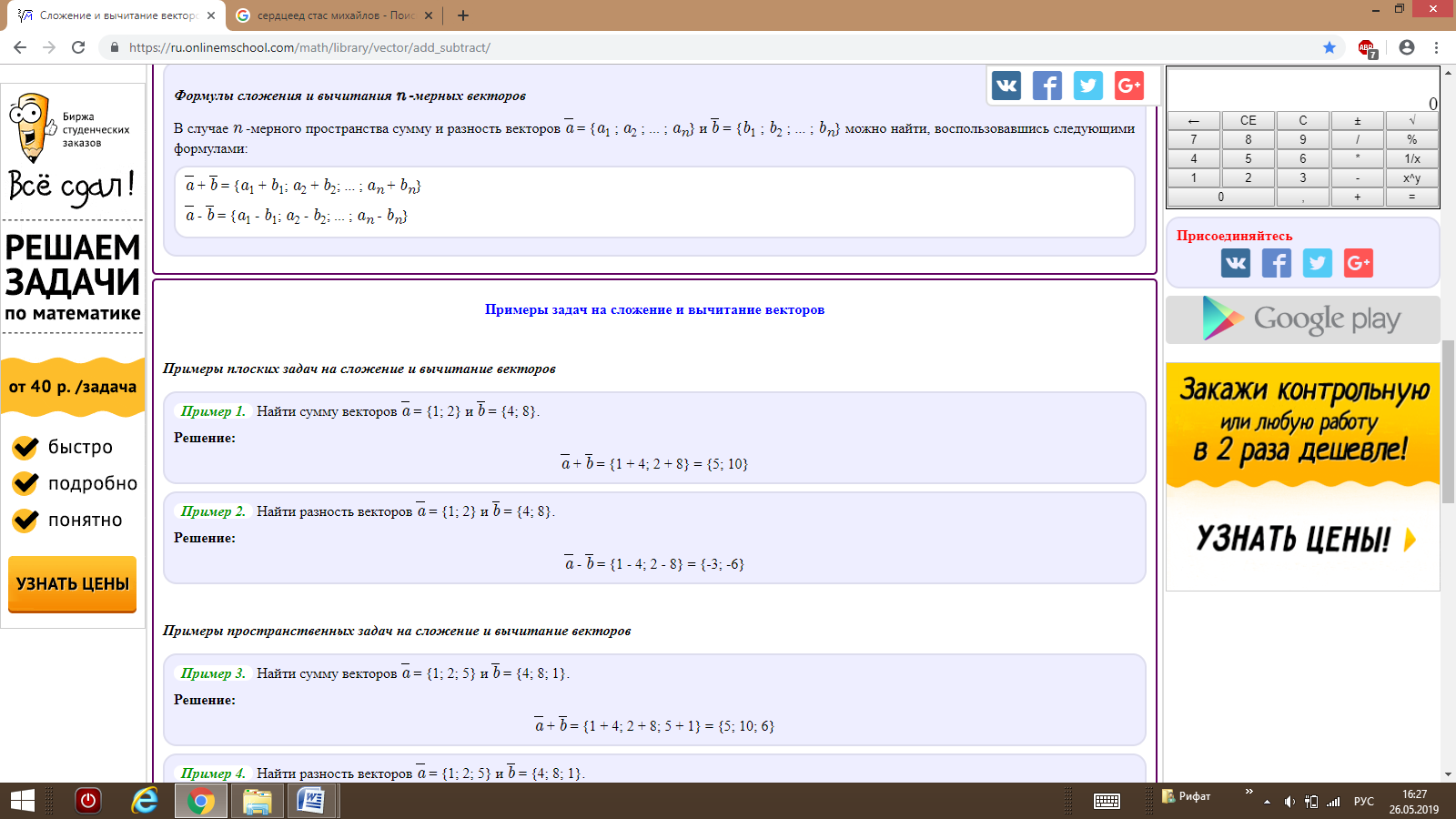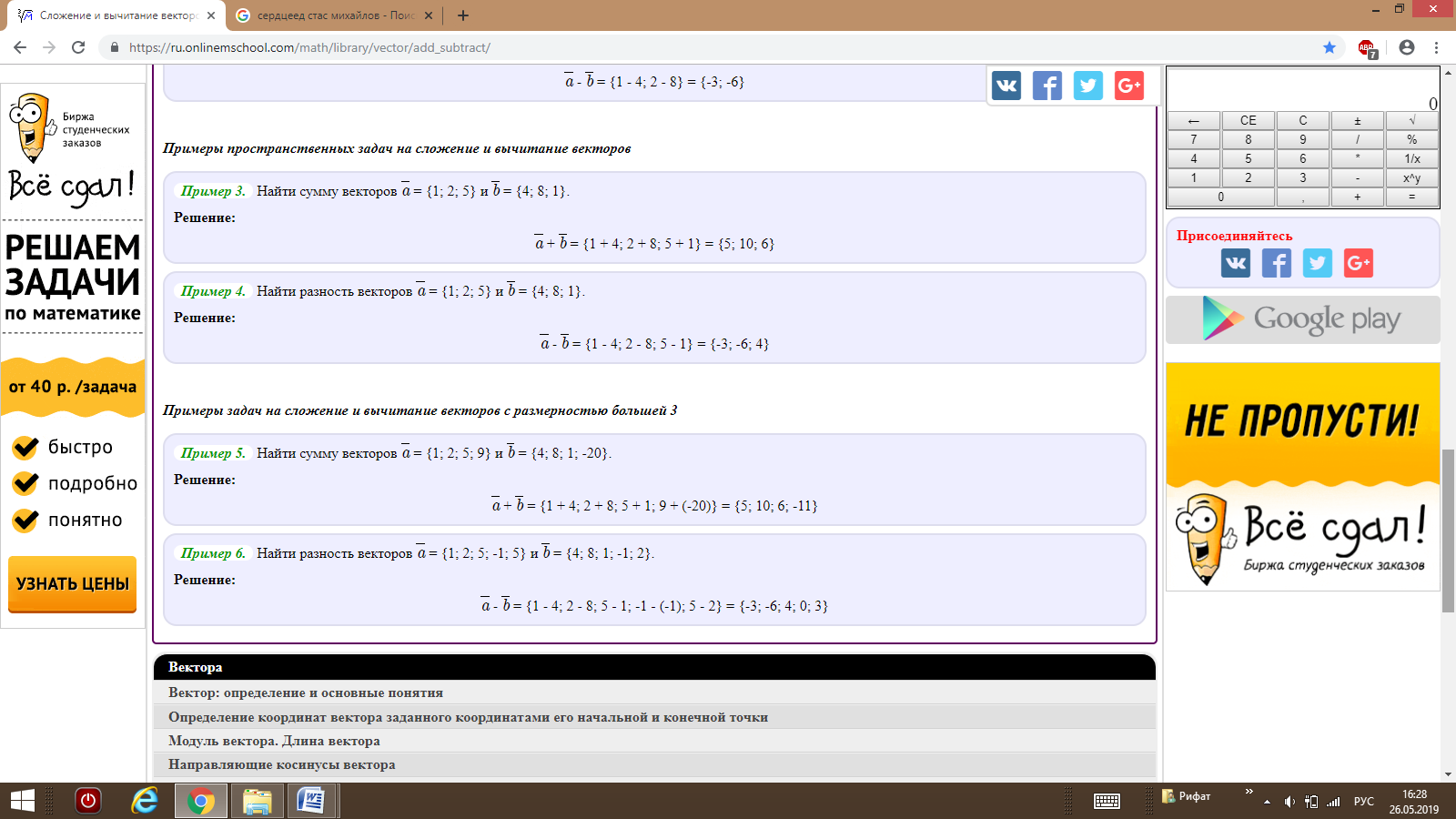