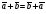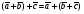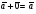Теория Векторы. Векторы (определение, изображение, равенство)
 Скачать 361.11 Kb. Скачать 361.11 Kb.
|
|
Векторы (определение, изображение, равенство). Из курса физики мы знаем, что есть величины, которые характеризуются числом в заданных единицах измерения (масса, время, расстояние, площадь), а для других необходимо задать число и направление (сила, скорость, давление). Первые величины называются скалярными, а вторыми векторными или векторами. Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Вектор – это философская категория, такая же как время, материя, пространство. Вектор в математике – это элемент векторного пространства. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор - с элементарно-геометрической точки зрения - есть геометрический объект, характеризуемый направлением (т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной.  Изображают вектор с помощью направленного отрезка. Если один конец отрезка считать его началом, а второй концом, то получается направленный отрезок. Рисуют отрезок со стрелкой от начала в конец. Обозначают вектор либо маленькими латинскими буквами со стрелкой  , ,  , либо , либо 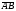 , т.е. отрезок с началом в точке А и концом в точке В. Две точки задают два разных (!) направленных отрезка , т.е. отрезок с началом в точке А и концом в точке В. Две точки задают два разных (!) направленных отрезка 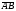 и и 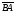 . . Модулем вектора считается длина отрезка AB и пишут 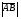 . . Особый случай нуль-вектор 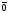 : его модуль равен нулю и направления он не имеет. Нуль вектор изображают точкой, которая рассматривается как начало и конец вектора. : его модуль равен нулю и направления он не имеет. Нуль вектор изображают точкой, которая рассматривается как начало и конец вектора. 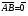 означает, что точки A и B совпадают. означает, что точки A и B совпадают.Два вектора называются коллинеарными, если изображающие их направленные отрезки лежат на параллельных прямых или на одной прямой. Для коллинеарных векторов принято обозначение 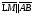 . .Два вектора называются ортогональными, если изображающие их направленные отрезки лежат на перпендикулярных прямых, что обозначают как 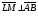 . . Пример 1: ABCD – прямоугольник. Укажите а) Вектор, коллинеарный вектору 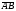 ; б) Вектор, ортогональный вектору ; б) Вектор, ортогональный вектору 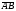 . .Решение: а) 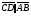 , , 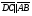 , , 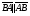 . .б) 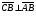 , , 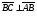 , , 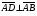 , , 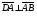 Коллинеарные векторы называются сонаправленными, если они лежат в одной полуплоскости относительно прямой соединяющей их начала либо один из лучей, задающих их направления, является подмножеством другого. Коллинеарные, но не сонаправленные векторы, называются противоположно направленными. Обозначения: 1) сонаправленные 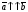 или или 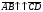 ; 2) противоположно направленные ; 2) противоположно направленные 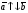 или или 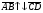 . .Сонаправленность векторов является отношением эквивалентности (т.е. выполнены свойства рефлексивности, симметричности, транзитивности). 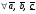 : :1. Рефлексивность 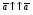 ; ; 2. Симметричность 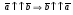 ; ; 3. Транзитивность 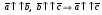 . . Пример 2. Точка M лежит на прямой AB. В каком случае векторы 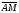 и и 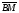 сонаправлены? сонаправлены?Решение: Если точка M лежит вне отрезка AB, то векторы 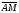 и и 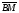 сонаправлены. Если точка M лежит внутри отрезка AB, то векторы сонаправлены. Если точка M лежит внутри отрезка AB, то векторы 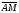 и и 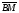 противоположно направлены. Если точка M – один из концов отрезка AB, то один из векторов противоположно направлены. Если точка M – один из концов отрезка AB, то один из векторов 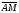 или или 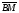 - нулевой, а для такого вектора понятие сонаправленности и противонаправленности не определены. - нулевой, а для такого вектора понятие сонаправленности и противонаправленности не определены. Пример 3. ABCD – прямоугольник. Укажите а) Вектор, сонаправленный вектору 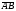 ; б) Вектор, противонаправленный вектору ; б) Вектор, противонаправленный вектору 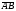 . .Решение: а) 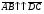 ; б) ; б) 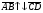 , , 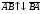 Два вектора называются равными, если 1) их длины равны 2) они сонаправлены. Обозначение 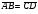 . .Укажем, как построить от выбранной точки C вектор, равный данному вектору 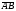 . .
Отметим, что равенство векторов – это отношение эквивалентности (т.е. верны свойства рефлексивности, симметричности, транзитивности). Пример 4: Пусть 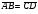 . Какие еще равные векторы можно задать этими точками A, B, C, D? . Какие еще равные векторы можно задать этими точками A, B, C, D?Решение: 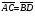 , , 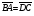 , , 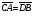 . .Тригонометрические функции углов от 90. Угол между векторами. 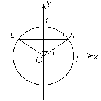 До сих пор мы определили тригонометрические функции только острых углов. Введем определения тригонометрических функций произвольных углов. Для этого рассмотрим в декартовой системе координат окружность с центром О и радиусом 1 (см. рисунок). Условимся откладывать углы от луча [OX) в верхнюю полуплоскость. Рассмотрим произвольный угол АОX = (A – точка пересечения стороны угла с окружностью). Тогда, cos = xA; sin = yA; tg = 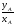 . Для острых углов эти определения совпадают с теми, которые даны в прямоугольном треугольнике. . Для острых углов эти определения совпадают с теми, которые даны в прямоугольном треугольнике.
Так как точки А и В симметричны относительно оси y, то cos(180 – ) = xB = – xA = – cos; sin(180 – ) = yB = yA = sin; tg(180 – ) = 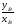 = – = –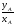 = – tg. Отметим, что синусы смежных углов равны, а косинусы смежных углов отличаются знаком. = – tg. Отметим, что синусы смежных углов равны, а косинусы смежных углов отличаются знаком.Вычислим тригонометрических функций угла 150: cos150 = cos(180 – 30) = –cos30 = 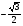 ; sin150 = sin(180 – 30) = sin30 = ; sin150 = sin(180 – 30) = sin30 = 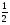 ; tg150 = tg(180 – 30) = –tg30 = ; tg150 = tg(180 – 30) = –tg30 = 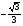 . .Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, причем от первого вектора ко второму против часовой стрелки (положительное направление). 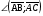 называется угол ВАС. называется угол ВАС.Угол между одинаково направленными векторами считается равным нулю, противоположно направленными 1800. Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Пример 5: Дан квадрат АВСD. Найдите:
 Операции над векторами. Над векторами определены операции сложения (в результате получаем вектор), вычитания (в результате получаем вектор), и 3 вида умножения: умножение на число (в результате получаем вектор), скалярное умножение (в результате получаем число, т.е. скаляр), векторное умножение (в результате получаем вектор). Сложение двух векторов осуществляют по правилу параллелограмма или по правилу треугольника. Правило параллелограмма: Отложим векторы  и и  от одной точки. Если векторы не коллинеарны, то их сумма представляется диагональю построенного на них параллелограмма, исходящая из общего начала векторов от одной точки. Если векторы не коллинеарны, то их сумма представляется диагональю построенного на них параллелограмма, исходящая из общего начала векторов  , ,  . Если вектора коллинеарны, то их сумма – коллинеарный им вектор, длина которого равна сумме длин векторов . Если вектора коллинеарны, то их сумма – коллинеарный им вектор, длина которого равна сумме длин векторов  и и  . .Правило треугольника: От конца вектора  откладываем вектор откладываем вектор  , тогда вектор , тогда вектор 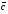 с началом первого вектора с началом первого вектора  и концом второго вектор и концом второго вектор  будет их сумма. будет их сумма.Правило цепочки при сложении векторов: Чтобы сложить несколько векторов удобно построить векторную ломанную (начало следующего вектора есть конец предыдущего вектора). Вектор от начала ломанной в ее конец и является суммой всех этих векторов. Если ломанная замкнулась, то сумма векторов равна 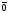 . .Два ненулевых вектора называются противоположными, если длины их равны, и они противоположно направлены. Вектор, противоположный вектору  обозначается – обозначается – . Нуль-вектор считается противоположным сам себе. Как при сложении противоположных чисел получается ноль, так и при сложении противоположных векторов получается нуль-вектор. . Нуль-вектор считается противоположным сам себе. Как при сложении противоположных чисел получается ноль, так и при сложении противоположных векторов получается нуль-вектор.Необходимое и Достаточное условие для того, чтобы векторы  и и  были противоположны были противоположны  + +  = = 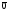  = – = – Как и вычитание чисел, вычитание векторов – это действие обратное сложению.  – –  = =  + (– + (– ), т.е. результат вычитания из вектора ), т.е. результат вычитания из вектора  вектора вектора  дает тот же результат, что сложение векторов дает тот же результат, что сложение векторов  и – и – . .Какие операции с векторными равенствами можно осуществлять на основании данных равенств? Перенос слагаемых из одной части в другую с противоположным знаком  – –  = = 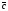 | | 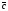 + +  = =  . .Правило вычитания векторов: Отложим векторы  и и  от одной точки, тогда вектор от конца вектора от одной точки, тогда вектор от конца вектора  к концу вектора к концу вектора  (направление от вычитаемого к уменьшаемому) будет их разностью. (направление от вычитаемого к уменьшаемому) будет их разностью.Отметим, что по неравенству треугольника можно утверждать, что 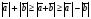 Пример 6: 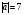 ; ; 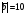 . Найдите границы изменения: а) . Найдите границы изменения: а) 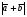 ; б) ; б) 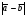 Решение: 3 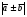 17 а) 3, если 17 а) 3, если 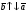 ; 17, если ; 17, если 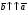 ; б) наоборот ; б) наоборотПример 7: Отметьте любые три точки A, B, C, не лежащие на одной прямой. Как найти точку X такую, что: a) 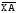 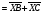 ; б) ; б) 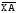 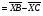 ; в) ; в) 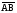 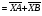 ; ; г) 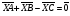 Решение: а), б), г) Точка X вершина параллелограмма XBAC; в) X=A; Если в сумме векторов одно и тоже слагаемое повторяется несколько раз, то, как и в алгебре чисел, такие суммы обозначаются через умножение. 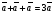 Произведением ненулевого вектора  на ненулевое число k называется вектор k на ненулевое число k называется вектор k для которого 1) его длина равна произведению длины вектора для которого 1) его длина равна произведению длины вектора  на модуль числа k; 2) он сонаправлен с на модуль числа k; 2) он сонаправлен с  , если k>0 и противоположно направлен, если k<0. Если , если k>0 и противоположно направлен, если k<0. Если 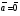 или k=0, то вектор k или k=0, то вектор k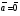 Запишем определение умножения вектора на число в краткой форме: 1. k 0 и 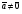 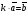 | | 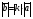 и если k > 0, то и если k > 0, то 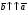 ; если k < 0, то ; если k < 0, то 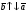 ; ;2. 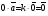 ; ;Пример 8: В трапеции ABCD основание BC=2 и AD=8, а диагонали пересекаются в точке O. Найдите такое число k, что 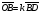 Решение: Треугольники BOC и DOA подобны с коэффициентом подобия BC:AD, т.е. 1:4. Следовательно OB:DO как соответствующие элементы в подобных треугольниках тоже как 1:4. Тогда BD в 5 раз больше OB. При этом 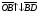 . . Тогда 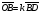 при k=-1/5 при k=-1/5Скалярным произведением двух ненулевых векторов называется число, равное произведению их модулей на косинус угла между ними. Если 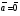 или или 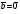 , то скалярное произведение равно нулю. , то скалярное произведение равно нулю.Запишем определение скалярного произведения векторов в краткой форме: 1) Если 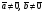 , то , то 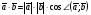 ; ;2) Если 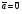 или или 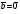 , то , то 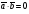 . .Обратите внимание, что произведением двух векторов является не вектор, а число! Пример 9: Сторона равностороннего треугольника ABC равна 2. Найдите скалярное произведение векторов 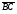 и и 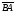 Решение: В равностороннем треугольника все углы 600. В зависимости от чертежа угол между векторами либо 600, либо (3600-600=3000), что не влияет на косинус угла, он в любом случае будет ½. Тогда по определению скалярного произведения 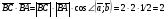 Векторное умножение не рассматривается в 9 классе, Вы будете знакомиться с ним на уроках физики и стереометрии. Сейчас Вы должны знать, что результатом векторного умножения двух векторов является вектор (!), ортогональный двум данным векторам, а обозначается векторное умножение «крестиком». Законы сложения векторов. Законы умножения векторов. Распределительные законы умножения относительно сложения. Сложение векторов подчиняется тем же законам, что и сложение чисел, а именно:
Умножение вектора на число тем же законам (похожие на законы сложения векторов и законы умножения чисел): 1. 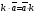 (переместительный закон или коммутативность); (переместительный закон или коммутативность);2. 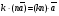 (сочетательный закон или ассоциативность). (сочетательный закон или ассоциативность).3. закон поглощения нуля или нулевого вектора - часть определения. Законы скалярного умножения. 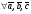 и kR и kR1) 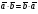 (из определения), (переместительный закон или коммутативность); (из определения), (переместительный закон или коммутативность);2) 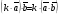 (из определения), (сочетательный закон или ассоциативность); (из определения), (сочетательный закон или ассоциативность);3) 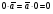 (из определения), закон поглощения нуля; (из определения), закон поглощения нуля;Распределительный закон умножения относительно сложения (дистрибутивность), а именно: 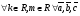 1) (k + m) 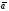 = k = k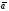 + m + m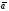 ; ; 2) k( 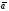 + + 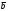 ) = k ) = k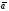 + k + k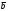 ; ;3) 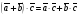 Рассмотренные законы позволяют работать с векторными выражениями как с обычными алгебраическими, в частности, можно умножать выражения, являющиеся линейными комбинациями векторов, по правилам умножения многочленов, использовать формулы сокращенного умножения, и т. д. Пример 10: 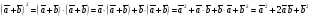 Пример 11: Упростить выражение 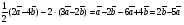 Пример 12: Из равенства 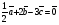 выразите каждый вектор через другие. выразите каждый вектор через другие.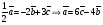 ; ; 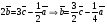 ; ; 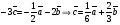 Пример 13: Докажите, что 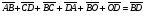 Решение: По коммутативности сложения векторов 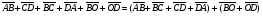 В первой скобке стоит замкнутая ломанная, и ее векторная сумма равна В первой скобке стоит замкнутая ломанная, и ее векторная сумма равна 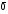 , а во второй скобке сумма равна вектору , а во второй скобке сумма равна вектору 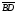 ч.т.д. ч.т.д. Признак коллинеарности векторов. Разложение вектора по двум неколлинеарным векторам. Признак коллинеарности векторов: Вектора  и и  коллинеарны тогда и только тогда, когда коллинеарны тогда и только тогда, когда  = k = k Если  = k = k , то коллинеарность , то коллинеарность  и и  следует из определения умножения вектора на число. следует из определения умножения вектора на число. Докажем обратное утверждение. Пусть 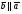 . Докажем, что kR | . Докажем, что kR | 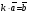 . . Если 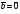 , то k = 0. 2) Если , то k = 0. 2) Если 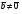 , то рассмотрим k | |k| = , то рассмотрим k | |k| = 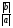 . Тогда . Тогда 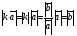 . Если . Если 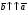 , то возьмем k > 0, тогда , то возьмем k > 0, тогда 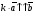 . Если . Если 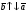 , то возьмем k < 0, тогда , то возьмем k < 0, тогда 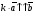 . Так как . Так как 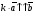 и и 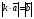 , то , то 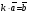 . . Замечание: Равенство 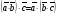 неверно; например, пусть неверно; например, пусть  и и 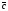 – не коллинеарны. – не коллинеарны. 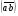 - это число и - это число и 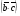 - число, тогда по признаку коллинеарности векторов - число, тогда по признаку коллинеарности векторов  и и 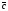 - коллинеарны, получили противоречие. - коллинеарны, получили противоречие.Пример 14: Доказать, что вектор 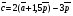 и вектор и вектор  коллинеарны. коллинеарны.Решение: Раскроем скобки и приведем подобные слагаемые, тогда 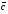 =2 =2 . Так как один вектор равен число, умноженное на другой вектор, то по признаку коллинеарности векторов эти вектора коллинеарны. . Так как один вектор равен число, умноженное на другой вектор, то по признаку коллинеарности векторов эти вектора коллинеарны.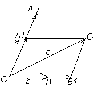 Теорема. 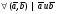 – не коллинеарны и – не коллинеарны и 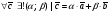 . .Доказательство. Существование. 1) Если 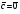 , то = 0; = 0; , то = 0; = 0; 2) Если 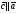 , то , то 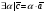 ; = 0; аналогично, если ; = 0; аналогично, если 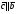 , то , то 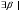 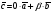 ; ; 3) Если 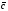 не коллинеарен ни не коллинеарен ни 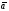 , ни , ни 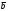 , то отложим эти три вектора от одной точки: , то отложим эти три вектора от одной точки: 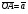 ; ; 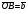 ; ; 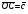 (см. рис. 2) и проведем (СА1) || (OB); (СB1) || (OA). OA1CB1 – пар-м, значит, (см. рис. 2) и проведем (СА1) || (OB); (СB1) || (OA). OA1CB1 – пар-м, значит, 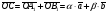 , так как , так как 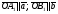 . .Единственность. Пусть 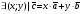 , тогда , тогда 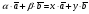 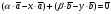 , то есть эти векторы – противоположны. Так как , то есть эти векторы – противоположны. Так как 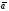 и и 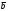 – не коллинеарны, то и полученные векторы – не коллинеарны, значит, они нулевые. Следовательно, – не коллинеарны, то и полученные векторы – не коллинеарны, значит, они нулевые. Следовательно, 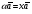 x = a и x = a и 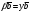 y = b, то есть (; ) – единственная] y = b, то есть (; ) – единственная] Доказанная теорема позволяет утверждать, что любая пара неколлинеарных векторов на плоскости является ее базисом. Принято говорить, что любой ненулевой вектор прямой может являться базисом прямой, так как любой другой вектор этой прямой можно выразить через него единственным образом. Принято говорить, что любая пара неколлинеарных векторов на плоскости является базисом плоскости, так как любой другой вектор этой плоскости можно выразить через данные два вектора единственным образом. Пример 15: АВС; М – середина [BC]; K[AC], |AK| : |KC| = 1 : 2. Выразите через 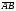 и и 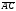 векторы: векторы: 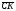 ; ;  ; ; 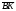 ; ;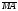 ; ; 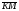 . . Решение: 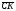 = = 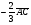 ; ; 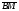 = = 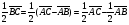 ; ; 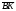 = = 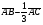 ; ; 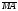 = = 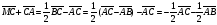 ; ; 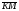 = = 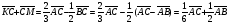 ; ; Установим важное векторное соотношение, которое поможет при решении задач.  Пусть дан [AB] и точка M[AB] | |AM| : |MB| = m : n. Рассмотрим произвольную точку О на плоскости и выразим 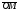 через через 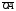 и и 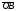 . . 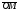 = = 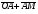 = = 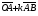 = = 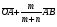 = = 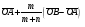 = = 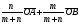 . .Можно осмыслить это векторное равенство как условие принадлежности точек M, A, B одной прямой AB. 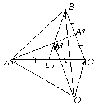 Пример 16: Пусть М – точка пересечения медиан АВС. Выразим 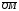 через через 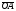 , , 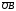 и и 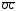 , где О – произвольная точка плоскости. Так как М[AA1] и |AM| : |MA1| = 2 : 1, то , где О – произвольная точка плоскости. Так как М[AA1] и |AM| : |MA1| = 2 : 1, то 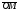 = = 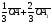 ; так как А1 – середина [BС], то ; так как А1 – середина [BС], то 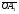 = = 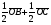 . Значит, . Значит, 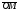 = = 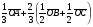 = = 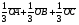 . . Является ли полученное разложение 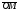 его разложением по базису? Нет, так как базисом на плоскости является пара неколлинеарных векторов. его разложением по базису? Нет, так как базисом на плоскости является пара неколлинеарных векторов.Из последнего равенства можно показать, что в любом треугольнике ABC для точки пересечения медиан M верно 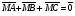 . Действительно, . Действительно, 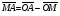 ; ; 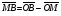 ; ;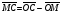 , тогда , тогда 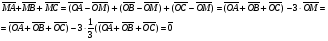 . 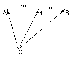 Свойства скалярного умножения векторов и признак ортогональности векторов. Отметим важные свойства скалярного умножения, которые являются следствием из определения скалярного умножения. 1) Если 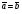 , то , то 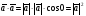 . Произведение вектора на себя называется скалярным квадратом вектора. Итак, . Произведение вектора на себя называется скалярным квадратом вектора. Итак, 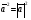 скалярный квадрат вектора равен квадрату длины вектора. скалярный квадрат вектора равен квадрату длины вектора.2) 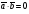 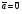 или или 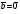 или или 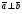 . Отметим, что если скалярное произведение двух ненулевых векторов равно нулю, то такие вектора ортогональны, так как в этом случае нулю должен равняется косинус угла между ними. Это свойство скалярного произведения называют Признак ортогональности векторов. . Отметим, что если скалярное произведение двух ненулевых векторов равно нулю, то такие вектора ортогональны, так как в этом случае нулю должен равняется косинус угла между ними. Это свойство скалярного произведения называют Признак ортогональности векторов.3) Если 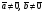 , то , то 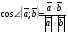 , следовательно: , следовательно: 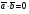 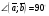 ; ; 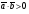 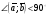 ; ; 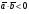 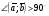 . .Пример 17: 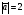 ; ; 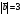 ; ; 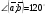 . Найти: а) . Найти: а) 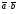 ; б) ; б) 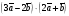 ; в) ; в) 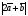 ; г) ; г) 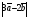 ; д) ; д) 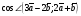 . .Решение: а) По определению скалярного умножения 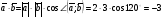 б) 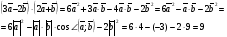 в) 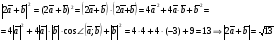 г) 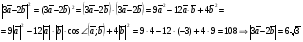 д) 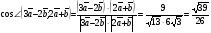 Пример 18: 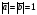 ; ; 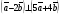 . Найти: . Найти: 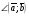 . .Решение: Заметим, что вектора 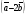 и и 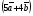 не нулевые. Если ненулевые вектора не нулевые. Если ненулевые вектора 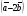 и и 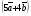 ортогональны, то по признаку ортогональности векторов их скалярное произведение равно нулю. Запишем скалярное произведение и приравняем нулю. ортогональны, то по признаку ортогональности векторов их скалярное произведение равно нулю. Запишем скалярное произведение и приравняем нулю. 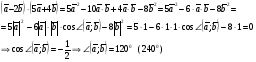 |

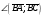
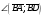
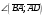
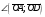
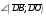
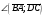
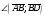
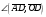
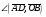
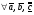 :
: