Лекции по векторной алгебре. Векторная алгебра основные понятия и определения определение 1
 Скачать 1.31 Mb.
|
|
Теорема 3 (пространственный случай). Если три вектора  ,  и  не компланарны, то любой четвертый вектор  можно представить единственным образом как линейную комбинацию первых трех векторов, т.е. ,где  скаляры.Доказательство. Приведем все векторы к общему началу  и построим параллелепипед, диагональю которого является вектор , а ребра  и  лежат на тех же прямых, что и векторы , и (рис.2.5). Основанием параллелепипеда является параллелограмм  . Докажем сначала, что вектор  .  По правилу параллелограмма  где  – вектор, совпадающий с диагональю параллелограмма ; вектор – диагональ параллелограмма, построенного на векторах  и  .Следовательно, Рис.2.5 Е 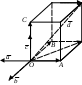  .Заметим, что  ,  ,  . Отсюда .  Подставляя  в  , получим .  Из построения следует, что разложение  единственно.2.5. Линейная зависимость и независимость векторов. Базис Пусть даны векторы  и скаляры  .Определение_1.'>Определение1. Векторы называются линейно независимыми, если их линейная комбинация равна нулевому вектору только при условии, что все ее коэффициенты равны нулю, т.е.   .  Определение2. Векторы  называются линейно зависимыми, если равенство  выполняется при условии, что хотя бы один из скаляров отличен от нуля.Замечание 1. Пусть, например, скаляр  . Тогда можно записать ,т.е. вектор  есть линейная комбинация векторов  .Таким образом, если система векторов линейно зависима, то по крайней мере один из векторов есть линейная комбинация остальных векторов и наоборот. Используя теоремы 1-3 о разложении вектора по направлению данных векторов можно доказать: два ненулевых вектора  и  коллинеарны, а три ненулевых вектора  и компланарны, если они линейно зависимы.Определение3. Любая пара неколлинеарных векторов и на плоскости или любая тройка некомпланарных векторов и в пространстве, заданных в определенном порядке, называются базисом множества векторов, лежащих соответственно на плоскости или в пространстве. Любой вектор на плоскости или в пространстве может быть представлен в виде линейной комбинации базисных векторов (согласно теоремам 2 и 3 раздела 2.4). Замечание 2. По теореме 2 (см. раздел 2.4) любой вектор , компланарный с неколлинеарными векторами и , можно представить в виде ,  т.е. вектор  разложен по базису  .По теореме 3 (раздел 2.4) любой вектор  может быть представлен в виде линейной комбинации трех некомпланарных векторов и : ,  т.е. вектор разложен по базису  .Определение4. Коэффициенты в разложениях вектора по базисным векторам называются координатами вектора в данном базисе и обозначаются  или  .Замечание 3. Задание вектора координатами полностью определяет вектор. Замечание 4. Из единственности разложения вектора по базису следует утверждение: если два вектора равны, то равны и их координаты в одном и том же базисе, и обратно. Замечание 5. Пусть дан базис  и в это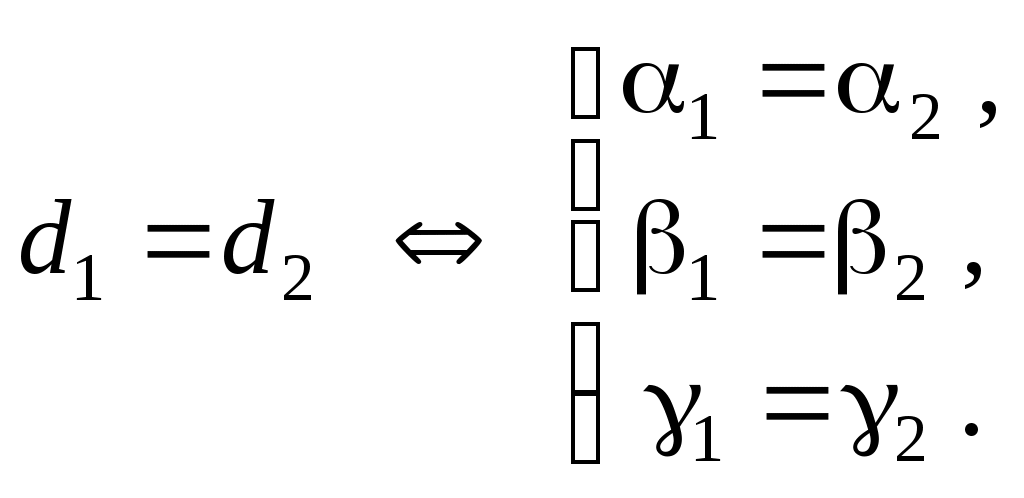м базисе – два вектора, заданные координатами и  .Тогда  Найдем произведение  :  .Отсюда  .Найдем сумму  : Тогда  .2.6. Проекция вектора на ось. Теоремы о проекциях Пусть дан вектор 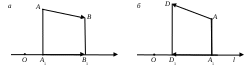 и некоторая ось  . Спроецируем вектор на ось и обозначим проекцию начала вектора на ось  , а проекцию конца вектора –  . Введем вспомогательный вектор  (рис.2.6, а). Рис.2.6 Определение1. Проекцией вектора  на ось называется длина отрезка оси  , взятая со знаком плюс, если вспомогательный вектор  и ось сонаправлены, и со знаком минус в противном случае (обозначение  ).Для вектора  (рис.2.6, б) в соответствии с определением имеем  .Из определения проекции следует: 1) проекция вектора – это скалярная величина, которая может быть положительной, отрицательной и равной нулю; 2) проекции равных векторов равны. Пусть даны два вектора и . Приведем их к общему началу так, чтобы  .Определение2. Углом  между двумя векторами называется наименьший угол, на который надо повернуть один из векторов, чтобы его направление совпало с направлением другого вектора. Из определения угла между двумя векторами следует, что  .Аналогично определяется угол между вектором и осью. Теорема 1. Проекция суммы векторов равна алгебраической сумме проекций слагаемых векторов. Доказательство. Пусть  (рис.2.7).Заметим, что  .  В соответствии с определением проекции вектора на ось, для данного расположения векторов имеем  ;    С учетом  равен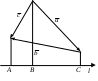ство  можно переписать в виде Рис.2.7  или  .Заменяя вектор , суммой  , окончательно получим .Замечание. Теорема обобщается на сумму любого конечного числа векторов: 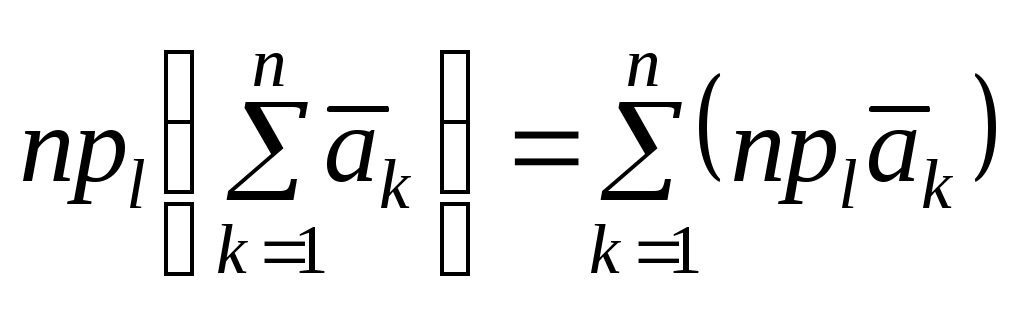 . 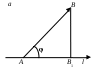 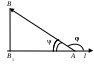Рис.2.8 Теорема 2. Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью. Доказательство. Рассмотрим два случая. 1 б . Пусть угол между вектором  и осью  острый  . Обозначим  проекцию точки  на ось (рис.2.8, а). По определению проекции вектора на ось  . Из прямоугольного треугольника  находим .2. Пусть угол между вектором и осью тупой: > π/2 (рис.2.8, б). Тогда ; .Окончательно  .Таким образом, теорема верна для любых углов, образованных вектором и положительным направлением оси .Следствие. Если  единичный вектор, то  . |