Лекции по векторной алгебре. Векторная алгебра основные понятия и определения определение 1

• Название: Векторная алгебра основные понятия и определения определение 1
• Дата: 25.11.2021
• Размер: 1.31 Mb.
• Имя файла: Лекции по векторной алгебре.doc
• Тип: Документы; #282243
• страница: 3 из 3

Теорема 3. Проекция произведения вектора на скаляр равна произведению скаляра на проекцию вектора на ось , т.е.

.

Доказательство. Приведем векторы и к общему началу. Рассмотрим два случая.

1. Пусть . Заметим, что векторы и сонаправлены. По теореме 2 можно записать

.

Итак,

.

2. Пусть . Векторы и в этом случае направлены противоположно. Поэтому

.

Окончательно

.

Таким образом, теорема верна для любого , как положительного, так и отрицательного.

2.7. Геометрический смысл координат

в ортогональном и нормированном базисе
Определение1. Три вектора и образуют правую тройку векторов, если с конца третьего вектора кратчайший поворот от первого вектора ко второму вектору виден происходящим против часовой стрелки (рис.2.9). В противном случае три вектора и образуют левую тройку векторов.

Рассмотрим декартову прямоугольную систему координат в пространстве . Введем орты положительных осей координат Векторы единичные и взаимно-перпендикулярные векторы. Эти векторы не компланарны и образуют базис в пространстве. Базис называют ортогональным и нормированным.

Определение 2. Прямоугольная система координат называется правой, если три вектора , образуют правую тройку векторов.

В дальнейшем будем использовать правую систему координат.

Пусть дан произвольный вектор в пространстве. Его можно единственным образом разложить по базису :

,

где ,  и γ – скаляры.

Как известно, коэффициенты при базисных векторах в разложении называются координатами вектора в базисе . Выясним их геометрический смысл. Для этого спроецируем равенство на ось . Применяя теоремы о проекциях, получим



Рис.2.9


.

Заметим, что

.

Равенство с учетом примет вид



Аналогично можно доказать, что



Введем для проекций вектора на оси декартовой системы координат следующие обозначения:

.

Разложение вектора по базису с учетом формул , и примет вид

.

Таким образом, координаты вектора в базисе есть его проекции на оси декартовой прямоугольной системы координат. Тот факт, что вектор задан своими проекциями, записывается в виде

.

Замечание 1. Возможно следующее представление вектора

.

Замечание 2. Пусть заданы два вектора 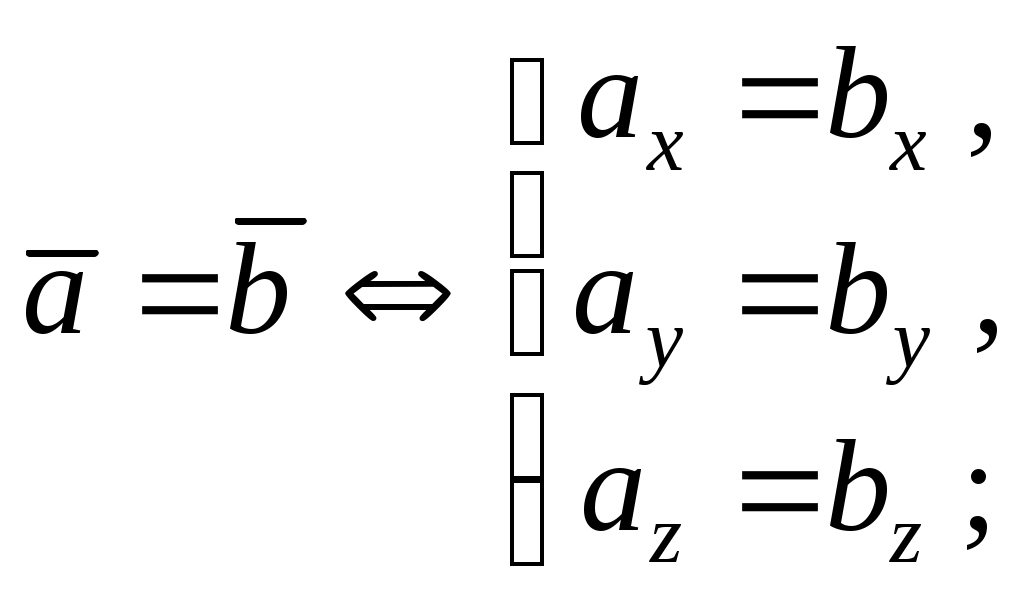и . Тогда действия над векторами, заданными своими проекциями на оси прямоугольной системы координат, определяются формулами

;

.

Замечание 3. По определению проекции вектора на ось имеем

.

Отсюда . Аналогично можно получить .

Определение 3. Косинусы углов, образованных вектором с положительным направлением осей координат, т.е. , , , называются направляющими косинусами вектора.

Замечание 4. Пусть два ненулевых вектора и коллинеарны. По теореме 1 (см. раздел 2.4) имеет место равенство

.

Из равенства векторов следует:



откуда

.

Таким образом, если два вектора коллинеарны, то их проекции на оси координат пропорциональны. Заметим, что если, например, , то и .

Замечание 5. Если единичный вектор, то

.

2.8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Определение. Скалярным произведением двух векторов и называется число, равное произведению их модулей на косинус угла между векторами, т.е.

.

Другие обозначения скалярного произведения: , , . Будем использовать обозначение .

Выясним механический смысл скалярного произведения. Пусть под действием постоянной силы точка перемещается по прямой линии из точки в точку (рис.2.10). Сила образует с прямой угол . Работа силы на указанном перемещении

.

Введем в рассмотрение вектор . Тогда

.

Свойства скалярного произведения следующие:

1. Из определения следует .

2. Скалярное произведение равно нулю, т.е. или , если хотя бы один из векторов нулевой:



Рис.2.10


или

или . В этом случае векторы и перпендикулярны.

Таким образом, ненулевые векторы и перпендикулярны, если их скалярное произведение равно нулю.

3. Рассмотрим скалярный квадрат вектора , т.е. скалярное произведение вектора на себя:

.

4. По теореме 2 (раздел 2.6)

.

Тогда



 или   (2.19)

5.

Доказательство.



6. .

7. Пусть векторы заданы координатами в базисе . Если

, ,

то







Замечание. Неподчеркнутые слагаемые равны нулю, так как скалярное произведение взаимно перпендикулярных ортов равно нулю, а в подчеркнутых слагаемых скалярный квадрат единичных векторов равен единице.

Итак,

.

Скалярное произведение двух векторов, заданных в базисе , равно сумме произведений одноименных координат (проекций).

Следствие 1. Модуль вектора, заданного в базисе , равен корню квадратному из суммы квадратов координат (проекций):



Следствие 2. Направляющие косинусы вектора, заданного в базисе 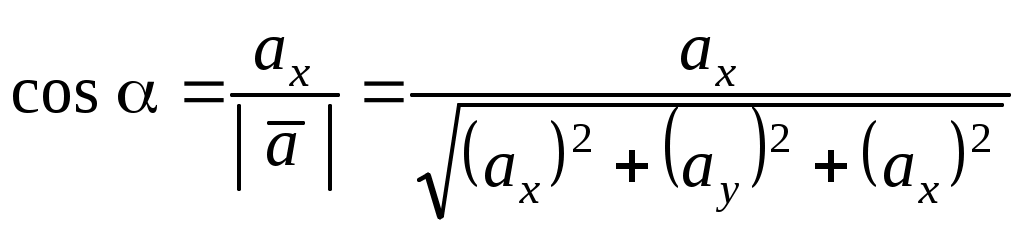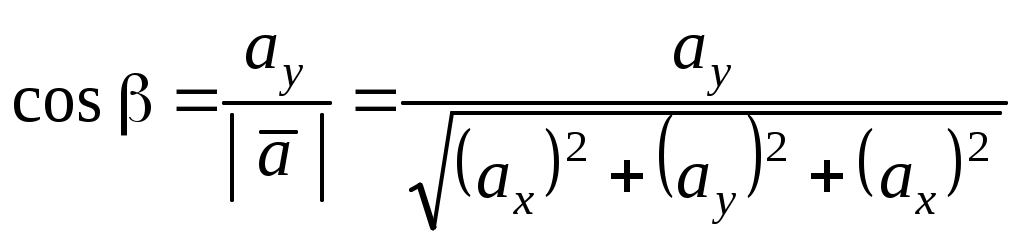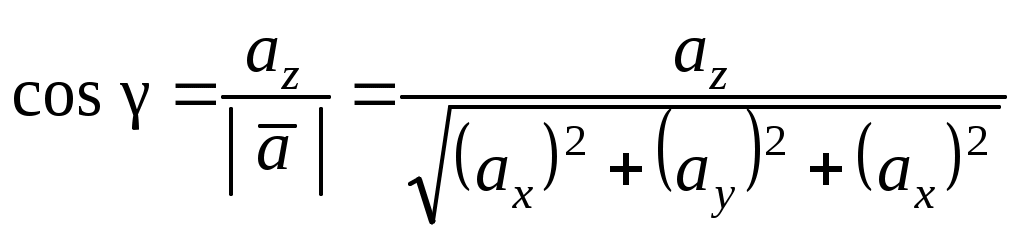, определяются по формулам

;

;

.

Следствие 3. Из определения скалярного произведения следует



или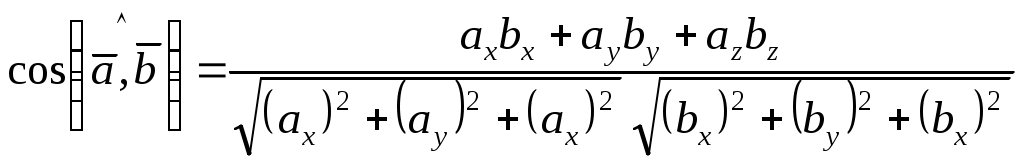

. (2.20)

2.9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Определение. Векторным произведением двух векторов и называется третий вектор , удовлетворяющий следующим условиям:

1) его модуль равен площади параллелограмма, построенного на данных векторах, как на сторонах;

2) вектор перпендикулярен плоскости параллелограмма;

3) вектор направлен таким образом, что три вектора образуют правую тройку векторов (рис.2.11).

Обозначение векторного произведения: , или . Будем использовать обозначение .




Из школьного курса математики известно, что площадь параллелограмма равна произведению двух сторон параллелограмма на синус угла, заключенного между ними. Отсюда модуль вектора определяется по формуле

.

Свойства векторного произведения следующие:

1. При перестановке сомножителей знак векторного произведения меняется на противоположный. Рассмотрим два вектора и . Из определения векторного произведения следует, что . Направления же векторов противоположны. Следовательно, , т.е. .

2. Если вектор , то равен нулю его модуль, т.е.

.

Этот результат возможен в двух случаях:

а) один из векторов нулевой:  или ;

б) синус угла между векторами равен нулю , следовательно, векторы и коллинеарные.

Таким образом, для коллинеарности двух ненулевых векторов необходимо и достаточно, чтобы их векторное произведение было равно нулю.

3. Из определения векторного произведения легко получить

.

4. Векторное произведение двух векторов обладает распределительным свойством:

.

5. Рассмотрим векторное произведение двух векторов, заданных в ортонормированном базисе :

; .

Предварительно выясним, чему равны векторные произведения ортов :

; ; ; ;

; ; ; ; .

Тогда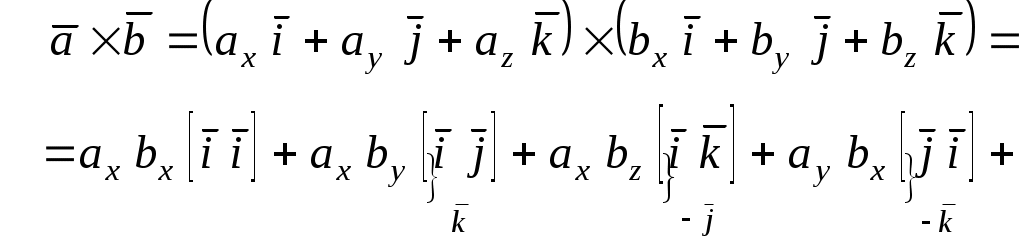



.

С учетом результатов векторного умножения ортов, приведенных выше, можно записать



или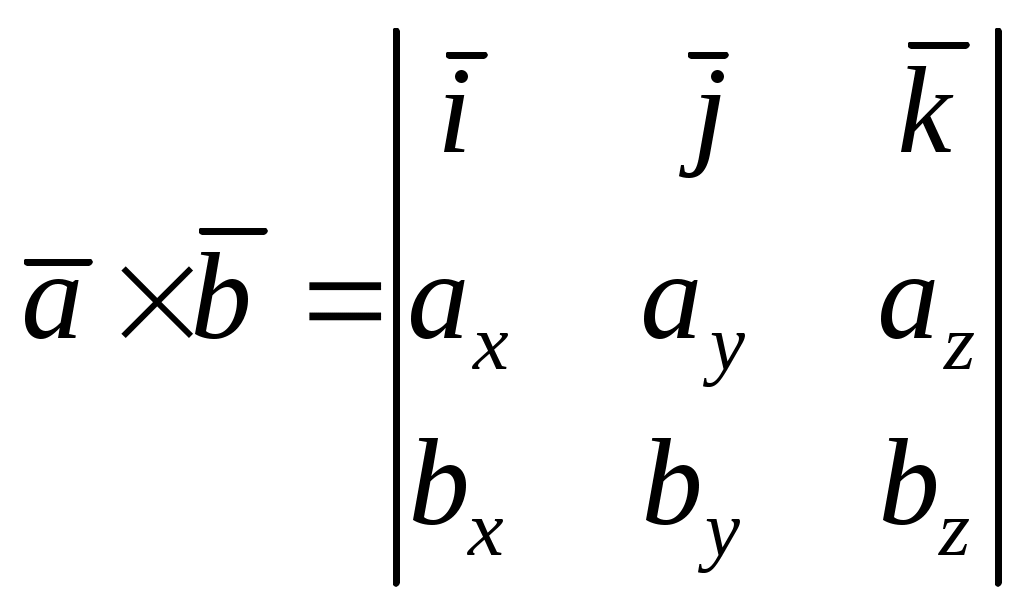

.



Рис.2.12


Замечание. Выясним механический смысл векторного произведения. Для этого рассмотрим следующую задачу. Твердое тело имеет одну неподвижную точку , а к точке тела приложена сила (рис.2.12). Воздействие силы на тело с неподвижной точкой характеризуется моментом силы относительно этой точки.

Ч
О
исловая мера момента (его модуль) равна произведению модуля силы на плечо, т.е. на расстояние от точки до линии воздействия силы . Модуль момента, таким образом, равен площади параллелограмма, построенного на векторах и . Направлен момент перпендикулярно плоскости, проходящей через точку и силу в ту сторону, откуда вращение тела вокруг точки , вызываемое силой , видно происходящим против часовой стрелки.

Следовательно, момент силы относительно точки есть векторное произведение вектора , соединяющего точку с точкой приложения силы, и вектора , т.е. .

2.10. Смешанное произведение трех векторов
Пусть даны три вектора: и . Перемножив два вектора и векторно, получим новый вектор . Этот новый вектор умножим скалярно на вектор . В результате получим скаляр, называемый смешанным или векторно-скалярным произведением данных векторов. Обозначение смешанного произведения векторов: , или

Установим геометрический смысл смешанного произведения. Пусть векторы и образу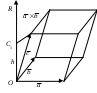ют правую тройку векторов. Обозначим . Приведем векторы к общему началу и на трех векторах как на ребрах построим параллелепипед (рис.2.13).



Рис.2.13


З аметим, что его объем , где и h – соответственно площадь основания параллелепипеда и его высота. С учетом определения и свойств векторного и скалярного произведений запишем

,



Итак,

.

Рассмотрим смешанное произведение . Заметим, что три вектора образуют левую тройку векторов. Обозначим

.

Тогда

,

.

Итак,

.

Отсюда

 или  

Таким образом, смешанное произведение векторов есть скаляр, модуль которого равен объему параллелепипеда, построенного на данных векторах. Этот скаляр положителен, если векторы образуют правую тройку векторов, и отрицателен в противном случае.

Свойства смешанного произведения следующие:

1. Круговая перестановка сомножителей в смешанном произведении не меняет его величины, так как при круговой перестановке сомножителей правая тройка векторов остается правой, а левая – левой, т.е.

.

2. Перестановка двух соседних сомножителей меняет знак смешанного произведения на противоположный, так как правая тройка векторов становится левой, а левая – правой, т.е.

.

3. Пусть смешанное произведение равно нулю, т.е. . Это возможно в следующих случаях:

1) ;

2) .

Отсюда следует, во-первых, что или , или ; во-вторых, , т.е. векторы и коллинеарные.

3. Скалярное произведение векторов и равно нулю, т.е.

.

Равенство возможно, если векторы или – нулевые векторы, что уже рассмотрено, или векторы и перпендикуляры.

Из определения векторного произведения следует, что вектор перпендикулярен векторам и . Следовательно, вектор должен быть перпендикулярен трем векторам и , что возможно, только если эти три вектора компланарны.

Таким образом, смешанное произведение обращается в нуль в трех случаях:

а) если один из векторов нулевой;

б) если любые два вектора коллинеарные;

в) если векторы векторам и компланарны.

4. Найдем смешанное произведение трех векторов, заданных своими координатами в базисе :

; ;

.

Известно, что векторное произведение определяется с помощью определителя третьего порядка: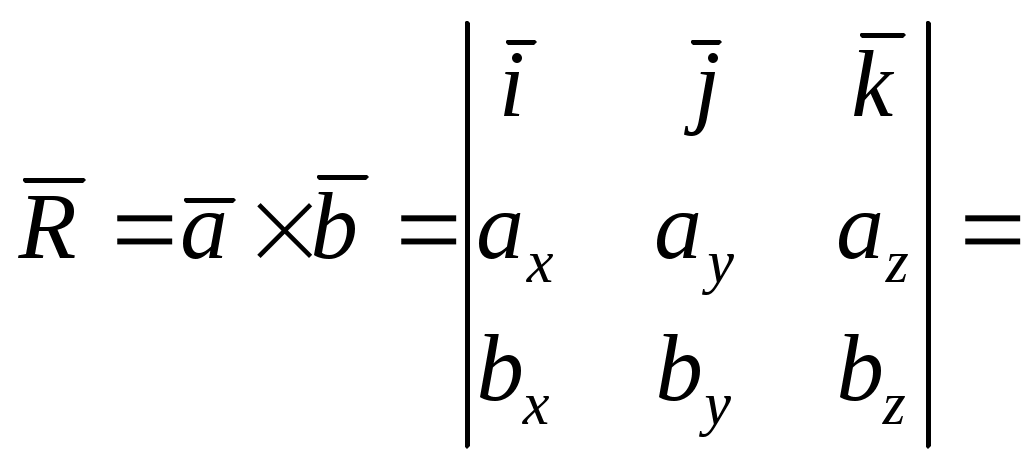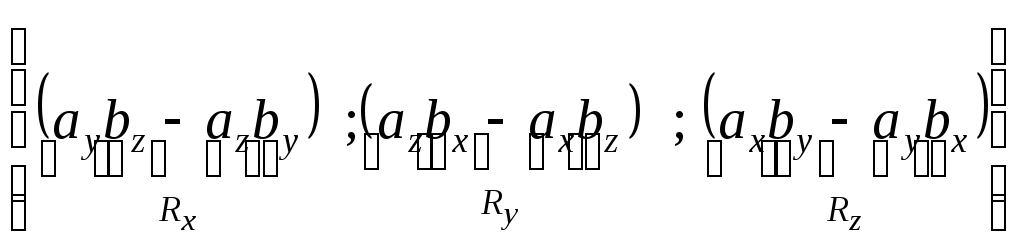

.

Скалярное произведение векторов и определяется по правилу

.

Следовательно,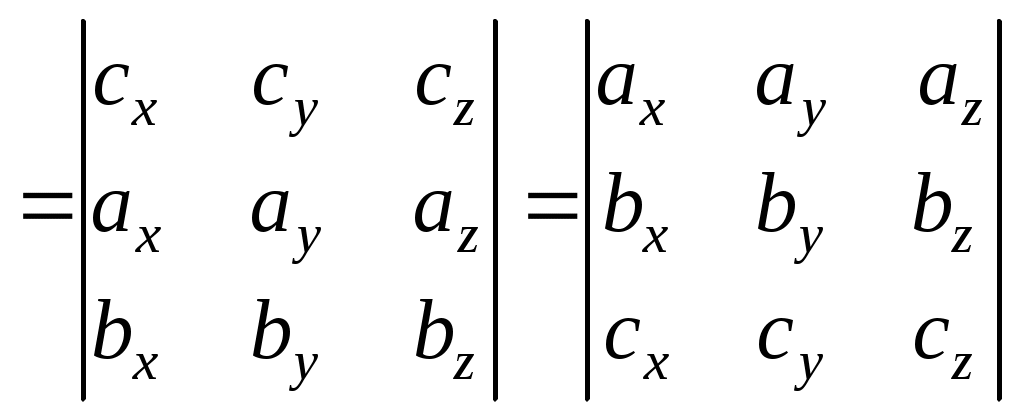



.

Итак,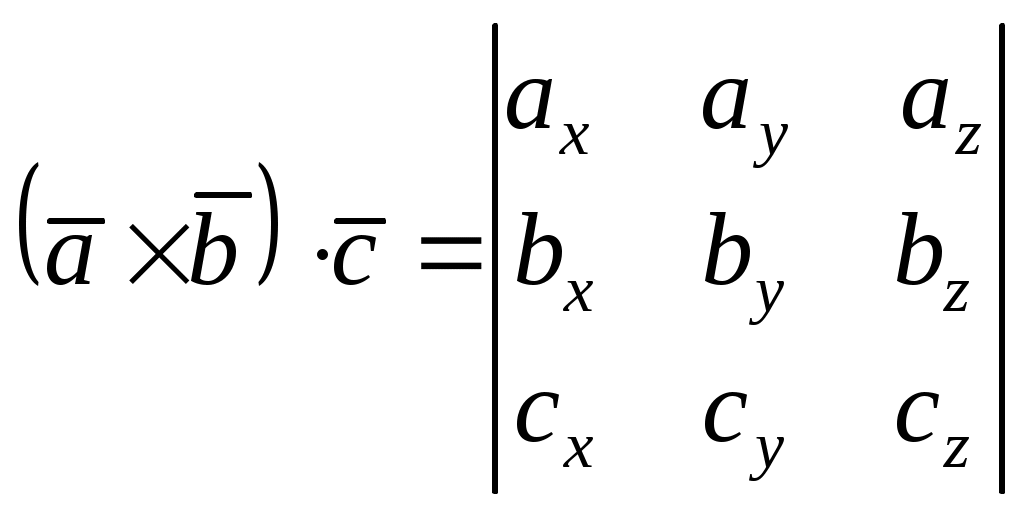

. (2.21)

Пример 2.1.Доказать, что векторы , и не компланарны при любом значении .

Решение. Известно, что три вектора компланарны, если их смешанное произведение равно нулю. Найдем смешанное произведение векторов 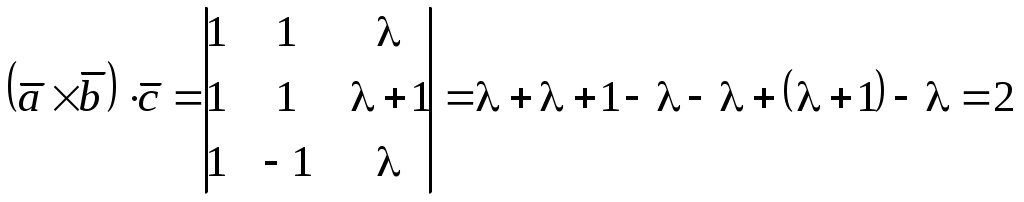, и по (2.21):

.

Так как определитель не равен 0 при любом , то и векторы , и не компланарны при любом .

Пример 2.2. Вершинами треугольной пирамиды являются точки: , , , . Найти:

1) объем пирамиды;

2) площадь треугольника , лежащего в основании пирамиды;

3) угол грани АВС и проекцию ребра АС на сторону основания АВ;

4) длину высоты, опущенной из вершины С на основание пирамиды;

Решение. 1. Объем пирамиды, построенной на векторах , составляет одну шестую часть от объема параллелепипеда, построенного на тех же векторах. Используя свойство смешанного произведения векторов, получим

.

Найдем координаты векторов: 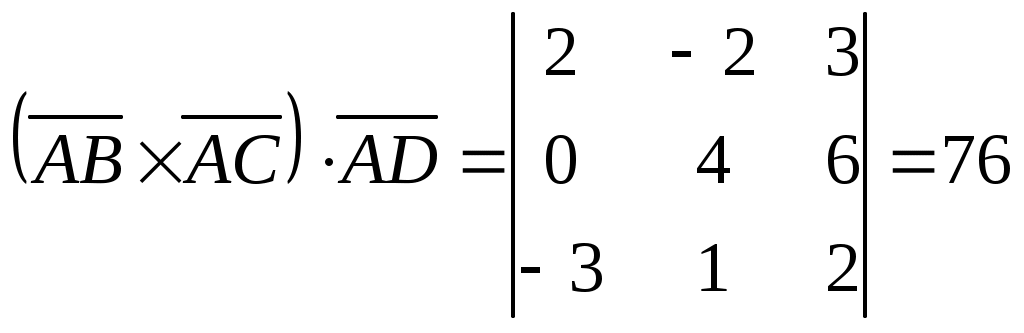(2; –2,3), (0; 4; 6), (–3; 1; 2). Их смешанное произведение

.

Объем пирамиды .

2. Площадь параллелограмма, построенного на двух векторах, исходящих из одной точки, равна модулю их векторного произведения. Площадь треугольника есть половина площади параллелограмма, поэтому площадь основания пирамиды можно найти как половину модуля векторного произведения векторов 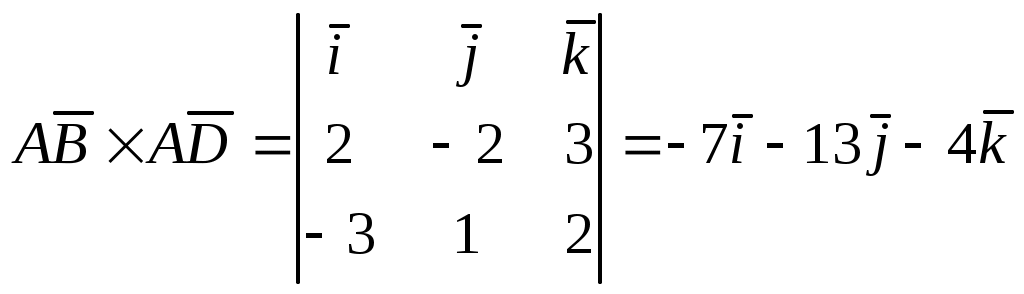и . Произведем соответствующие вычисления:



Длина этого вектора



Тогда



3. Угол грани АВС можно рассматривать, как угол между векторами и , и использовать для его нахождения формулу (2.20):



.

Проекцию ребра АС на сторону основания АВ найдем по (2.19)



4. Как известно, объем пирамиды, равен одной трети произведения площади ее основания на высоту, т.е.



.

Вопросы для самопроверки
1. Что такое вектор? Какие существуют линейные операции над векторами?

2. Как определяется базис и координаты вектора в базисе?

3. Какой базис называется ортонормированным?

4. Как осуществляются арифметические операции над векторами, заданными своими координатами?

5. Каков геометрический смысл координат вектора в ортонормированном базисе?

6. Что называется проекцией вектора на ось ?

7. Как определяется скалярное произведение двух векторов?

8. Каков физический смысл скалярного произведения векторов?

9. Каковы основные свойства скалярного произведения?

10. При каком условии скалярное произведение векторов обращается в нуль?

11. Что называется векторным произведением векторов?

12. При каком условии векторное произведение векторов обращается в нуль?

13. Каков геометрический смысл модуля векторного произведения векторов?

14. Каков механический смысл векторного произведения векторов?

15. Каковы основные свойства векторного произведения?

16. Что называется смешанным произведением векторов?

17. Какие основные свойства смешанного произведения вы знаете?

18. Каков геометрический смысл смешанного произведения векторов?

19. При каких условиях смешанное произведение векторов обращается в нуль?

20. Как определить, могут ли три вектора образовывать базис, если они заданы своими координатами в ортонормированном базисе?

Тесты

№ п/п	Вопрос	Варианты ответа
1	Даны векторы и . Площадь параллелограмма, построенного на этих векторах как на сторонах, равна	1. 2. 3. 4.
		Продолжение таблицы
№ п/п	Вопрос	Варианты ответа
2	Каким из перечисленных свойств не обладает векторное произведение двух ненулевых векторов и	1. 2. 3. 4.
3	Если , , то чему равно	1. 14 2. 5 3. 4. 11
4		1. 2. 3. 0 4. –3
5	Векторы	1. Равны 2. Компланарные 3. Коллинеарные 4. Единичные
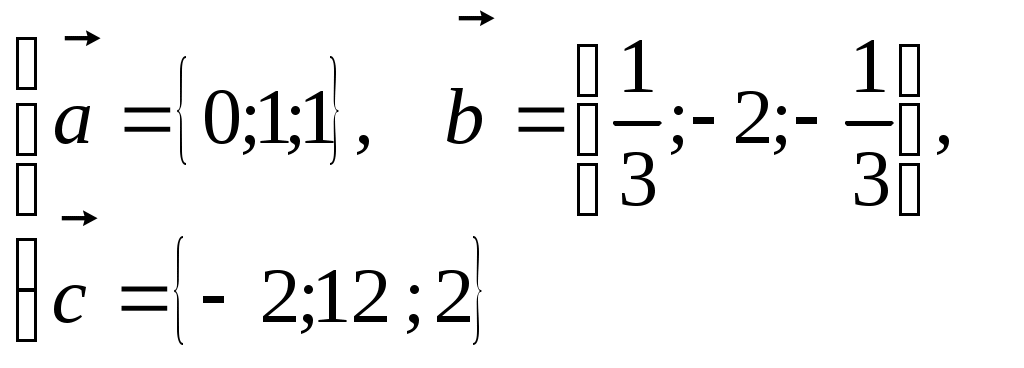
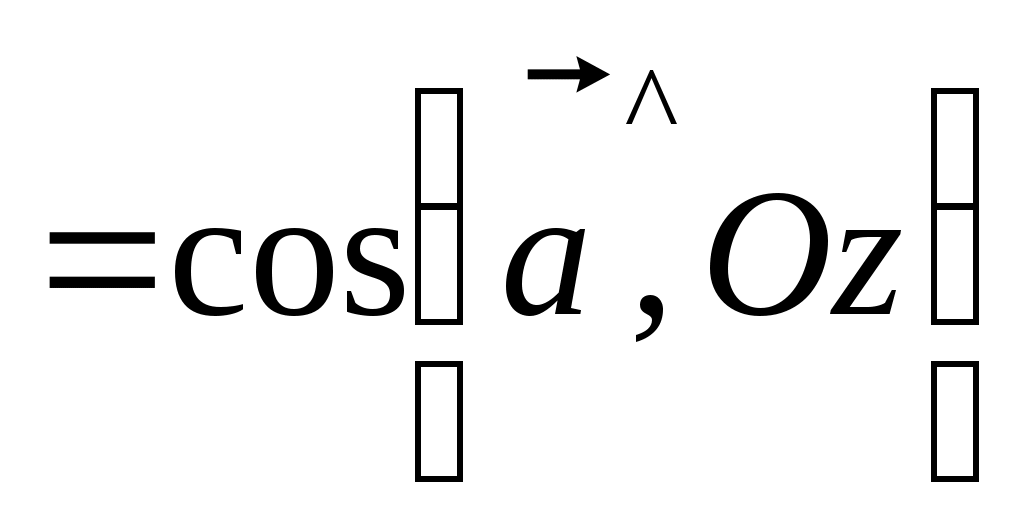6	Направляющий косинус cos = радиуса-вектора точки равен	1. 4 2. 4/5 3. 3/5 4. 0
7	Указать верную формулу	1. 2. 3. 4.
8	Даны три вектора , причем векторы коллинеарные. Указать, какое из предложенных соотношений неверно.	1. 2. 3. 4.
		Окончание таблицы
№ п/п	Вопрос	Варианты ответа
9	Площадь треугольника, образованного векторами и , равна	1. 1 2. 2 3. 3 4. 3/2
10	Даны векторы и . Тогда проекция вектора на ось Ox равна	1. –4 2. 4 3. 13 4. –13